江苏省扬州市江都区八校联谊2022-2023学年九年级下学期第一次月考数学试卷

试卷更新日期：2023-04-28 类型：月考试卷

进入出卷网下载

一、单选题

1. 某路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当小明到达该路口时，遇到红灯的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{5}{12}$ C、 $\frac{1}{2}$ D、1

查看试题解析
2. 如图，AB $∥$ CD $∥$ EF.若 $\frac{A C}{C E}$ ＝ $\frac{1}{2}$ ， BD＝4，则DF的长为（）

A、2 B、4 C、6 D、8

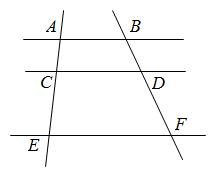查看试题解析
3. 将二次函数 $y = 2 x^{2}$ 的图象先向左平移1个单位，再向上平移3个单位，得到的函数图象的表达式为（）

A、 $y = 2 (x + 1)^{2} + 3$ B、 $y = 2 (x - 1)^{2} + 3$ C、 $y = 2 (x + 1)^{2} - 3$ D、 $y = 2 (x - 2)^{2} - 3$

查看试题解析
4. 已知一元二次方程 $x^{2} - 3 x + 1 = 0$ 有两个实数根 $x_{1} 、 x_{2}$ ，则 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为（）

A、6 B、2 C、4 D、3

查看试题解析

5. 表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数（cm）	180	185	185	180
方差	3.6	3.6	7.4	8.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

6. 如图，已知 $⊙ O$ 是 $△ A B D$ 的外接圆， $A B$ 是 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的弦， $∠ A B D = 56 °$ ，则 $∠ B C D$ 等于（）

A、 $30 °$ B、 $32 °$ C、 $34 °$ D、 $36 °$

查看试题解析
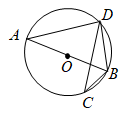7. 已知二次函数的图象如下所示，下列5个结论：① $a b c > 0$ ；② $b - a - c > 0$ ；③ $4 a + c > - 2 b$ ；④ $3 a + c > 0$ ；⑤ $a + b > m (a m + b)$ ( $m \neq 1$ 的实数)，其中正确的结论有几个？

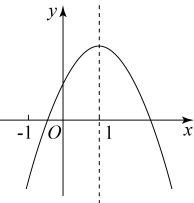A、①②③ B、②③④ C、②③⑤ D、③④⑤

查看试题解析
8. 如图，在边长为8的正方形 $A B C D$ 中， $E$ 、 $F$ 分别是边 $A B$ 、 $B C$ 上的动点，且 $E F = 6$ ， $M$ 为 $E F$ 中点， $P$ 是边 $A D$ 上的一个动点，则 $C P + P M$ 的最小值是（）

A、10 B、 $8 \sqrt{5} - 3$ C、 $6 \sqrt{5} + 3$ D、 $3 \sqrt{3} + 5$

查看试题解析

二、填空题

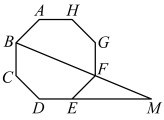
9. 若 $⊙ O$ 的直径为 $5 c m$ ，点A到圆心O的距离为 $3 c m$ ，那么点A与 $⊙ O$ 的位置关系是：点A在 $⊙ O$ .（填“上”、“内”、“外”）

查看试题解析
10. 在某次招聘测试中，小华的笔试成绩为90分，面试成绩为85分，若笔试成绩、面试成绩按 $6 ： 4$ 计算平均成绩，则小华的平均成绩是分.

查看试题解析
11. 若线段 $A B = 6 c m$ ，点C是线段 $A B$ 的一个黄金分割点（ $A C > B C$ ），则 $B C$ 的长为 $c m$ （结果保留根号）.

查看试题解析
12. 加工爆米花时，爆开且不糊的粒数的百分比称为“可食用率”．在特定条件下，可食用率y与加工时间x（单位：min）满足函数表达式y=-0.3x²+1.5x-1，则最佳加工时间为min．

查看试题解析
13. 用半径为4，圆心角为90°的扇形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径为.

查看试题解析
14. 如图，在正八边形 $A B C D E F G H$ 中，对角线 $B F$ 的延长线与边 $D E$ 的延长线交于点M，则 $∠ M$ 的度数为.

查看试题解析
15. 如图，路灯距离地面8米，身高1.6米的小明站在距离灯的底部（点O）20米的A处，则小明的影子AM长为米．

查看试题解析
16. 若关于 $x$ 的一元二次方程 $(k - 2) x^{2} + 4 x + 2 = 0$ 有实数根，则 $k$ 的取值范围是.

查看试题解析
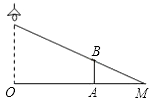17. 如图，在边长为6的等边△ABC中，D是边BC上一点，将△ABC沿EF折叠使点A与点D重合，若BD ： DE=2 ： 3，则CF=.

查看试题解析
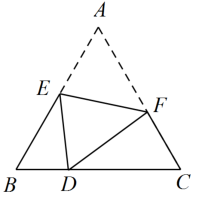18. 如图，将矩形 $O A B C$ 置于平面直角坐标系中，B点坐标为 $(10 ， 7)$ ，点D为BC上一点，且 $D C = 2$ ，连接AD，将 $△ A B D$ 沿AD折叠，压平，使B点的对应点E落在坐标平面内.若抛物线 $y = a x^{2} - 8 a x + 10$ （ $a \neq 0$ ，a为常数）的顶点落在 $△ A D E$ 的内部（不含边界），则a的取值范围为.

查看试题解析

三、解答题

19.

(1)、解方程： $x^{2} + 6 x - 7 = 0$

(2)、计算： $4 s i n 45 ° - \sqrt{8} + {(\sqrt{3} - 1)}^{0} - t a n 30 °$

查看试题解析
20. 我区某校七（2）班组织了一次朗读比赛，甲、乙两队各10人的比赛成绩（10分制）如下表（单位：分）：
甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9

(1)、计算乙队成绩的平均数和方差；

(2)、已知甲队成绩的方差是1.4，哪一队的成绩较为整齐？

查看试题解析
21. 周末期间，电影院正热映国产影片A《你好，李焕英》、B《唐人街探案3》和国外影片C《银行家》，甲、乙两人分别从三部电影中随机选择一部观看.

(1)、甲选择B《唐人街探案3》观看的概率为；

(2)、请用列表或画树状图的方法求甲、乙两人都选择观看国产电影的概率.（请用画树状图或列表的方法写出分析过程）

查看试题解析
22. 如图，在直角坐标系中，边长为1的小正方形组成的网格中，给出了格点△ABC（顶点为网格线的交点），在给定的网格中，解答下列问题：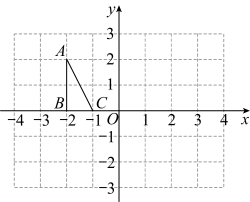
⑴以A为位似中心，将△ABC按相似比2：1放大，得到△AB₁C₁ ，画出△AB₁C₁.
⑵以C₁为旋转中心，将△AB₁C₁顺时针旋转90°，得到△A₁B₂C₁.
①画出△A₁B₂C₁；
②求点A的运动路径长.

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，过点A作 $A E ⊥ B C$ ，垂足为E，连接 $D E$ ， F为线段 $D E$ 上一点，且 $∠ A F E = ∠ B$ .

(1)、求证： $△ A D F ∽ △ D E C$ ；

(2)、若 $A B = 8 ， A D = 12 ， A F = 6$ ，求 $A E$ 的长.

查看试题解析
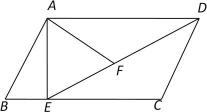24. 如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A、D的⊙O分别交边AB、AC于点E、F.

(1)、求证：BC是⊙O的切线；

(2)、若 $B E = 4$ ， $s i n B = \frac{1}{2}$ ，求阴影部分的面积.

查看试题解析
25. 北京冬奥会推出的吉祥物“冰墩墩”“雪容融”深受人们的喜爱，销售火爆.某经销商以60元/个的价格购进了一批“冰墩墩”摆件，打算采取线下和线上两种方式销售，调查发现线下每周销售量y个与售价x元/个（ $x > 60$ ）满足一次函数关系：
售价x（元/个）
…
80
90
100
…
销量y（个）
…
400
300
200
…
线下销售，每个摆件的利润不得高于进价的80%；线上售价为100元/个，供不应求.

(1)、求y与x的函数表达式；

(2)、若该经销商共购进“冰墩墩”1000个，一周内全部销售完.如何分配线下和线上的销量，可使全部售完后获得的利润最大，最大利润是多少？（不计其它成本）

查看试题解析
26. 定义一种新的运算方式： $C_{n}^{2} = \frac{n (n - 1)}{2}$ （其中 $n \geq 2$ ， n为正整数），例如 $C_{3}^{2} = \frac{3 (3 - 1)}{2} = 3$ ， $C_{5}^{2} = \frac{5 (5 - 1)}{2} = 10$ .

(1)、若 $C_{n}^{2} = 45$ ，求 $n$ 的值；

(2)、记 $C_{n}^{2} = y$ ，当 $y \geq 153$ 时，求 $n$ 的取值范围.

查看试题解析
27. 如图①，在矩形 $A B C D$ 中，动点P从A出发，以相同的速度沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x， $△ P A B$ 面积为y，y与x的函数图象如图②所示.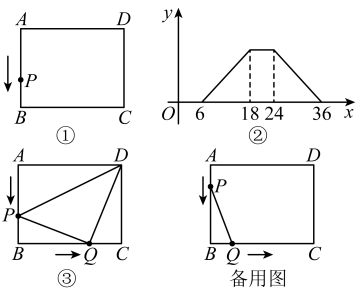

(1)、矩形 $A B C D$ 的面积为；

(2)、如图③，若点P沿 $A B$ 边向点B以每秒1个单位的速度移动，同时点Q从点B出发沿 $B C$ 边向C以每秒2个单位的速度移动.如果P、Q两点在分别到达B、C两点后就停止移动，回答下列问题：
①当运动开始 $1.5$ 秒时，试判断 $△ D P Q$ 的形状；
②在运动过程中，是否存在这样的时刻，使以Q为圆心， $P Q$ 的长为半径的圆与矩形 $A B C D$ 的对角线 $A C$ 相切，若存在，求出运动时间；若不存在，请说明理由.

查看试题解析
28. 当直线y＝kx＋b（k、b为常数且k≠0）与抛物线y＝ax²＋bx＋c（a、b、c为常数，且a≠0）有唯一公共点时，叫做直线与抛物线相切，直线叫做抛物线的切线，这个公共点叫做切点，其切点坐标（x，y）为相应方程组 ${\begin{array}{l} y = k x + b \\ a x^{2} + b x + c \end{array}$ 的解.如将直线y＝4x与抛物线y＝x²＋4，联合得方程组 ${\begin{array}{l} y = 4 x \\ y = x^{2} + 4 \end{array}$ ，从而得到方程x²＋4＝4x，解得x₁＝x₂＝2，故相应方程组的解为 ${\begin{array}{l} x_{1} = x_{2} = 2 \\ y_{1} = y_{2} = 8 \end{array}$ ，所以，直线y＝4x与抛物线y＝x²＋4相切，其切点坐标为（2，8）.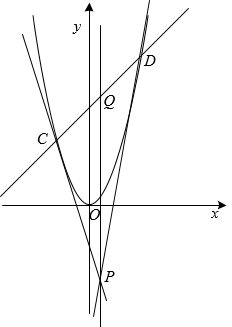

(1)、直线m：y＝2x-1与抛物线y＝x²相切吗？如相切，请求出切点坐标；

(2)、在（1）的条件下，过点A（1，-3）的直线n与抛物线y＝x²也相切，求直线n的函数表达式，并求出直线m与直线n的交点坐标；

(3)、如图，已知直线y＝kx＋3（k为常数且k≠0）与抛物线y＝x²交于C、D，过点C、D分别作抛物线的切线，这两条切线交于点P，过点P作x轴的垂线交CD于点Q，试说明点Q是CD的中点.

查看试题解析

售价x（元/个）	…	80	90	100	…
销量y（个）	…	400	300	200	…