江苏省东台市第五教育联盟2022-2023学年九年级下学期第一次月质量检测数学试题
试卷更新日期:2023-04-28 类型:月考试卷
一、单选题
-
1. 的相反数是( )A、2 B、 C、-2 D、2. 在下列四个几何体中,主视图与俯视图都是圆的为( )A、
 B、
B、 C、
C、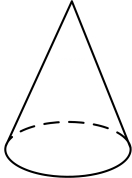 D、
D、 3. 下列各式的计算中正确的是( )A、 B、 C、 D、4. 港珠澳大桥是连接香港、珠海和澳门的超大型跨海通道,总长55000米.数据55000米用科学记数法表示为( )A、5.5×104米 B、5.5×103米 C、0.55×104米 D、55×103米5. 数据6,4,5,4,6,2,6的众数是( )A、2 B、4 C、5 D、66. 如图,的三个顶点在上,是直径,点C在上,且 , 则等于( )
3. 下列各式的计算中正确的是( )A、 B、 C、 D、4. 港珠澳大桥是连接香港、珠海和澳门的超大型跨海通道,总长55000米.数据55000米用科学记数法表示为( )A、5.5×104米 B、5.5×103米 C、0.55×104米 D、55×103米5. 数据6,4,5,4,6,2,6的众数是( )A、2 B、4 C、5 D、66. 如图,的三个顶点在上,是直径,点C在上,且 , 则等于( )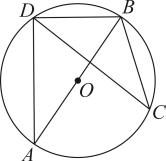 A、 B、 C、 D、7. 一元二次方程有两个不相等的实数根,则k的取值范围是( )A、 B、且 C、 D、且8. 已知二次函数 , 将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线与新图像有3个交点时,m的值是( )
A、 B、 C、 D、7. 一元二次方程有两个不相等的实数根,则k的取值范围是( )A、 B、且 C、 D、且8. 已知二次函数 , 将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线与新图像有3个交点时,m的值是( )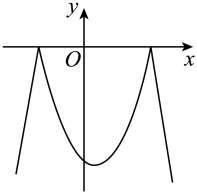 A、 B、-2 C、-2或3 D、-6或-2
A、 B、-2 C、-2或3 D、-6或-2二、填空题
-
9. 使 有意义的x的取值范围是 .
10. 分解因式:3a2-3 .11. 双曲线y= 在每个象限内,函数值y随x的增大而增大,则m的取值范围是 .
12. 已知圆锥的底面圆半径是3,高为4,则圆锥的侧面积是.13. 若正多边形的一个外角是45°,则该正多边形的边数是 .14. 一元二次方程的两个根为 , 则.15. 定义:在中, , 把∠A的邻边与对边的比叫做的余切,记作.等腰三角形中有两条边为4和6,则底角的余切值为.16. 如图, 中, , , ,若D,E是边 上的两个动点,F是边 上的一个动点, ,则 的最小值为.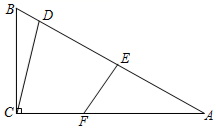
三、解答题
-
17. 计算:18. 解不等式组:19. 先化简,再求值: ,其中 .20. 有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为的值,两次结果记为(1)、用树状图或列表法表示所有可能出现的结果;(2)、若表示平面直角坐标系的点,求点在第三象限的概率.21. 某校为了了解学生的安全意识,在全校范围内随机抽取部分学生进行问卷调查.根据调查结果,把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制如下两幅尚不完整的统计图.
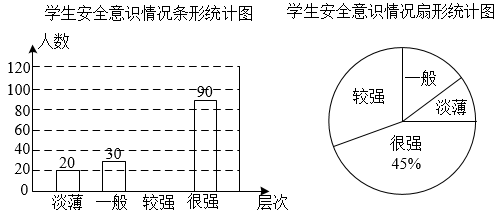
根据以上信息,解答下列问题:
(1)、这次调查一共抽取了 ▲ 名学生,将条形统计图补充完整;(2)、扇形统计图中,“较强”层次所占圆心角的大小为;(3)、若该校有1900名学生,现要对安全意识为“淡薄”、“一般”的学生强化安全教育,根据调查结果,请你估计全校需要强化安全教育的学生人数.22. 如图,在中,E是的中点,连接并延长交的延长线于点F.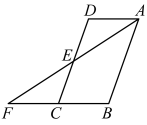 (1)、求证:;(2)、若 , .求的度数.23. 如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为37°,此时教学楼顶端G恰好在视线DH上,再向前走8米到达B处,又测得教学楼顶端G的仰角∠GEF为45°,点A、B、C三点在同一水平线上.
(1)、求证:;(2)、若 , .求的度数.23. 如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高1.5米的测角仪测得古树顶端H的仰角∠HDE为37°,此时教学楼顶端G恰好在视线DH上,再向前走8米到达B处,又测得教学楼顶端G的仰角∠GEF为45°,点A、B、C三点在同一水平线上.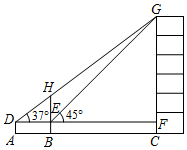
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、求古树BH的高;(2)、计算教学楼CG的高度.24. 如图,是的直径,弦平分. (1)、过点作的切线 , 交于点(用直尺和圆规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,连接 , 与相似吗?为什么?25. 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题:
(1)、过点作的切线 , 交于点(用直尺和圆规作图,不写作法,保留作图痕迹);(2)、在(1)的条件下,连接 , 与相似吗?为什么?25. 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: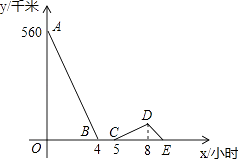 (1)、甲乙两地之间的距离为千米;(2)、求快车和慢车的速度;(3)、求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.26. 如图
(1)、甲乙两地之间的距离为千米;(2)、求快车和慢车的速度;(3)、求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.26. 如图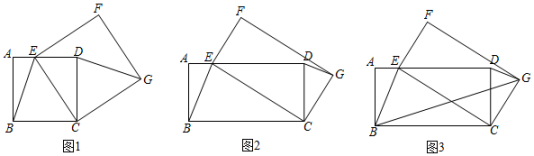 (1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为.27. 如图,已知抛物线 与x轴交于 、 两点,与y轴交于C点,设抛物线的顶点为D.过点D作 轴,垂足为E.P为线段DE上一动点, 为x轴上一点,且 .
(1)、【问题情境】如图1,四边形ABCD是正方形,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE,则DG与BE的数量关系是;(2)、如图2,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接DG、BE.判断线段DG与BE有怎样的数量关系和位置关系,并说明理由;(3)、【拓展提升】如图3,在(2)的条件下,连接BG,则2BG+BE的最小值为.27. 如图,已知抛物线 与x轴交于 、 两点,与y轴交于C点,设抛物线的顶点为D.过点D作 轴,垂足为E.P为线段DE上一动点, 为x轴上一点,且 .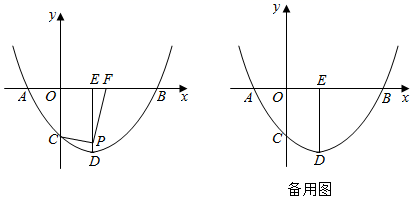 (1)、求抛物线的解析式:(2)、①当点P与点D重合时,求m的值;
(1)、求抛物线的解析式:(2)、①当点P与点D重合时,求m的值;②在①的条件下,将 绕原点按逆时针方向旋转 并平移,得到 ,点C,O,F的对应点分别是点 , , ,若 的两个顶点恰好落在抛物线上,直接写出点 的坐标;
(3)、当点P在线段DE上运动时,求m的变化范围.