山西省太原市2022-2023学年高一下学期数学期中试卷
试卷更新日期:2023-04-28 类型:期中考试
一、单选题
-
1. 复数的共轭复数为( )A、 B、 C、 D、2. 已知向量满足 , , 则( )A、6 B、8 C、10 D、123. 已知复数 , 则下列说法正确的是( )A、的虚部为4 B、复数在复平面内对应的点位于第三象限 C、 D、4. 已知向量 , , 若 , 则与夹角的余弦值为( )A、 B、 C、 D、5. 已知一圆锥的母线长为 , 侧面积为 , 则该圆锥的高为( )A、2 B、 C、4 D、106. 在四边形中,若 , 且 , 则该四边形是( )A、正方形 B、菱形 C、矩形 D、等腰梯形7. 在边长为2的正方形中,点为边上的动点,点为边上的动点,且 , 则的最小值为( )A、6 B、5 C、4 D、38. 已知的面积为 , , , 则( )A、 B、 C、 D、29. 用斜二测画法画水平放置的平面图形的直观图时,下列结论正确的是( )A、三角形的直观图是三角形 B、平行四边形的直观图是平行四边形 C、正方形的直观图是正方形 D、菱形的直观图是菱形
二、多选题
-
10. 已知复数、 , 则下列结论正确的是( )A、 B、若 , 则 C、若 , 则、中至少有个是 D、若且 , 则11. 在直角坐标系xOy中,已知点 , 则( )A、若 , 则 B、若点P在BC上,则 C、若 , 则 D、若在方向上的投影向量是 , 则12. 半正多面体亦称“阿基米德多面体”,是由边数不全相同的正多边形围成,体现了数学的对称美.如图,二十四等边体就是一种半正多面体,是由正方体截去八个一样的四面体得到的,若它的所有棱长都为 , 则( )
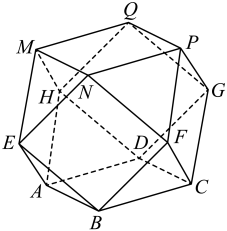 A、被截正方体的棱长为2 B、被截去的一个四面体的体积为 C、该二十四等边体的体积为 D、该二十四等边体外接球的表面积为
A、被截正方体的棱长为2 B、被截去的一个四面体的体积为 C、该二十四等边体的体积为 D、该二十四等边体外接球的表面积为三、填空题
-
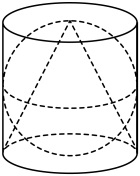
13. 设复数满足 , 则.14. 如图所示的图案,是由圆柱、球和圆锥组成,已知球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面,则图案中圆锥、球、圆柱的体积.
 15. 如图,从气球 上测得正前方的河流的两岸 , 的俯角分别为75°,30°,此时气球的高是 ,则河流的宽度 等于.
15. 如图,从气球 上测得正前方的河流的两岸 , 的俯角分别为75°,30°,此时气球的高是 ,则河流的宽度 等于.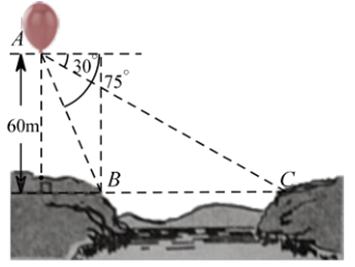 16. 已知向量 且 ,则 的取值范围是 .
16. 已知向量 且 ,则 的取值范围是 .四、解答题
-
17. 已知复数 , 且为纯虚数.(1)、求实数的值;(2)、设复数 , 且复数对应的点在第二象限,求实数的取值范围.18. 如图,在中,已知 , BC,AC边上的中线AM,BN相交于点P.设 .
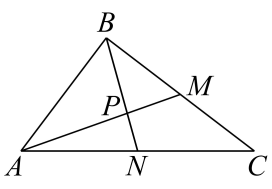 (1)、用表示;(2)、求 .19. 如图,矩形是用斜二测画法画出的水平放置的一个平面四边形的直观图,其中 , .
(1)、用表示;(2)、求 .19. 如图,矩形是用斜二测画法画出的水平放置的一个平面四边形的直观图,其中 , . (1)、画出平面四边形的平面图,并计算其面积;(2)、若该四边形以为轴,旋转一周,求旋转形成的几何体的体积和表面积.20. 的内角、、的对边分别为、、 , 已知向量与向量共线.(1)、求;(2)、若的面积为 , , 求的值.21. 的内角的对边分别为 , 已知向量与向量共线.(1)、求;(2)、若的面积为 , 求周长的取值范围.22. 如图所示,是一块三角形空地,其中 , , .当地政府计划将这块空地改造成一个休闲娱乐场所,拟在中间挖一个人工湖 , 其中、在边上,且 , 挖出的泥土堆放在地带形成假山,剩下的地带建成活动场所.
(1)、画出平面四边形的平面图,并计算其面积;(2)、若该四边形以为轴,旋转一周,求旋转形成的几何体的体积和表面积.20. 的内角、、的对边分别为、、 , 已知向量与向量共线.(1)、求;(2)、若的面积为 , , 求的值.21. 的内角的对边分别为 , 已知向量与向量共线.(1)、求;(2)、若的面积为 , 求周长的取值范围.22. 如图所示,是一块三角形空地,其中 , , .当地政府计划将这块空地改造成一个休闲娱乐场所,拟在中间挖一个人工湖 , 其中、在边上,且 , 挖出的泥土堆放在地带形成假山,剩下的地带建成活动场所.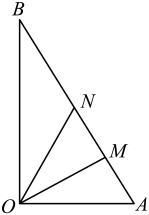 (1)、当时,求的长度;(2)、若要求挖人工湖用地的面积是堆假山用地面积的倍,试确定的大小.23. 如图所示,是一块三角形空地,其中 , , .当地政府规划将这块空地改造成一个休闲娱乐场所,拟在中间挖一个人工湖 , 其中在边上,且 , 挖出的泥土堆放在地带上形成假山,剩下的地带建成活动场所.
(1)、当时,求的长度;(2)、若要求挖人工湖用地的面积是堆假山用地面积的倍,试确定的大小.23. 如图所示,是一块三角形空地,其中 , , .当地政府规划将这块空地改造成一个休闲娱乐场所,拟在中间挖一个人工湖 , 其中在边上,且 , 挖出的泥土堆放在地带上形成假山,剩下的地带建成活动场所.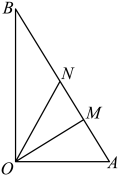 (1)、若要求挖人工湖用地的面积是堆假山用地面积的倍,试确定的大小;(2)、为节省投入资金,人工湖的面积要尽可能小,问如何设计施工方案,可使的面积最小?最小面积是多少?
(1)、若要求挖人工湖用地的面积是堆假山用地面积的倍,试确定的大小;(2)、为节省投入资金,人工湖的面积要尽可能小,问如何设计施工方案,可使的面积最小?最小面积是多少?