江苏省苏州市2022-2023学年高一下学期数学期中试卷
试卷更新日期:2023-04-28 类型:期中考试
一、单选题
-
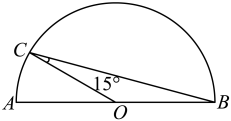
1. 已知复数 , 则的虚部为( )A、 B、 C、-1 D、12. 是所在平面上一点,若 , 则是的( )A、外心 B、内心 C、重心 D、垂心3. 已知复数满足 , 则的最小值为( )A、 B、 C、 D、4. 欧拉公式是由18世纪瑞士数学家、自然科学家莱昂哈德・欧拉发现的,被誉为数学上优美的公式.已知 , 则( )A、 B、 C、 D、5. 在如图所示的半圆中,为直径,为圆心,点为半圆上一点且 , , 则等于( )
 A、 B、 C、 D、6. 在中,若 , 则的形状为( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形7. 点是所在平面内一点且满足 , 则下列说法正确的个数有( )
A、 B、 C、 D、6. 在中,若 , 则的形状为( )A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等腰三角形或直角三角形7. 点是所在平面内一点且满足 , 则下列说法正确的个数有( )①若 , 则点是边的中点;②若点是边上靠近点的三等分点,则;③若点在边的中线上且 , 则点是的重心;④若 , 则与的面积相等.
A、1个 B、2个 C、3个 D、4个8. 在中, , 边上的高等于 , 则的值为( )A、 B、 C、 D、二、多选题
-
9. 若关于的方程的一个根是 , 则下列说法中正确的是( )A、 B、 C、的共轭复数在复平面内对应的点在第二象限 D、在复平面内对应的两点间的距离为10. 下列命题正确的是( )A、非零向量和不共线,若 , 则、、三点共线 B、已知和是两个夹角为的单位向量,且 , 则实数 C、若四边形满足 , 则该四边形一定是矩形 D、点在所在的平面内,动点满足 , 则动点的运动路径经过的重心11. 在中, , 则下列说法正确的是( )A、有两解 B、边上的高为 C、的长度为 D、的面积为12. 已知函数 , 则下列说法正确的是( )A、在区间上单调递增 B、的对称轴是 C、方程在的解为 , 且 D、若 , 则
三、填空题
-
13. 下面给出的几个关于复数的命题,
①若是纯虚数,则实数
②复数是纯虚数
③复数在复平面内对应的点位于第三象限
④如果复数满足 , 则的最小值是2
以上命题中,正确命题的序号是.
14. 已知的最大值为 , 则.15. 是钝角三角形,内角所对的边分别为 , 则最大边的取值范围为.16. 根据毕达哥拉斯定理,以直角三角形的三条边为边长作正方形,从斜边上作出的正方形的面积正好等于在两直角边上作出的正方形面积之和.现在对直角三角形按上述操作作图后,得如图所示的图形,若 , 则 .
四、解答题
-
17. 已知复数(其中是虚数单位,).(1)、若在复平面内表示的点在第三象限的角平分线上,求实数的值;(2)、若 , 求实数的取值范围.18. 已知函数图象的相邻两对称轴间的距离为.(1)、求的解析式;(2)、将函数的图象向左平移个单位长度,再把所得图象上各点的横坐标缩小为原来的(纵坐标不变),得到函数的图象,求的单调递减区间.19. 设是虚数,是实数且.(1)、求的值以及实部的取值范围;(2)、若 , 求证:为纯虚数.20. 如图,一个直径为的水车按逆时针方向每分钟转1.8圈,水车的中心距离水面的高度为 , 水车上的盛水筒到水面的距离为(单位:)(在水面下则为负数),若以盛水筒刚浮出水面时开始计时,则与时间(单位:)之间的关系为.
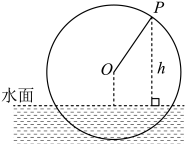 (1)、求与的函数解析式;(2)、求在一个旋转周期内,盛水筒在水面以上的时长.
(1)、求与的函数解析式;(2)、求在一个旋转周期内,盛水筒在水面以上的时长.
