吉林省白山市2023届高三下学期数学四模联考(4月期中)试卷
试卷更新日期:2023-04-28 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知 , 为纯虚数,则( )A、2 B、3 C、4 D、53. 设的内角A,B,C的对边分别为a,b,c,若 , , , 则( )A、 B、 C、 D、4. 函数的图象可能为( )A、
 B、
B、 C、
C、 D、
D、 5. 已知圆与圆外切,直线与圆C相交于A,B两点,则( )A、4 B、2 C、 D、6. 在正三棱柱中, , , 以为球心,为半径的球面与侧面的交线长为( )A、 B、 C、 D、7. 甲、乙、丙三人玩传球游戏,每个人都等可能地把球传给另一人,由甲开始传球,作为第一次传球,经过3次传球后,球回到甲手中的概率为( )A、 B、 C、 D、8. 已知双曲线的左、右焦点分别为 , , P是双曲线E上一点, , 的平分线与x轴交于点Q, , 则双曲线E的离心率为( )A、 B、2 C、 D、
5. 已知圆与圆外切,直线与圆C相交于A,B两点,则( )A、4 B、2 C、 D、6. 在正三棱柱中, , , 以为球心,为半径的球面与侧面的交线长为( )A、 B、 C、 D、7. 甲、乙、丙三人玩传球游戏,每个人都等可能地把球传给另一人,由甲开始传球,作为第一次传球,经过3次传球后,球回到甲手中的概率为( )A、 B、 C、 D、8. 已知双曲线的左、右焦点分别为 , , P是双曲线E上一点, , 的平分线与x轴交于点Q, , 则双曲线E的离心率为( )A、 B、2 C、 D、二、多选题
-
9. 给出下列说法,其中正确的是( )A、若 , 则 B、若 , 则 C、若 , 则的最小值为2 D、若 , 则的最小值为210. 十项全能是田径运动中全能项目的一种,是由跑、跳、投等个田径项目组成的综合性男子比赛项目,比赛成绩是按照国际田径联合会制定的专门田径运动会全能评分表将各个单项成绩所得的评分加起来计算的,总分多者为优胜者.如图,这是某次十项全能比赛中甲、乙两名运动员的各个单项得分的雷达图,则下列说法正确的是( )
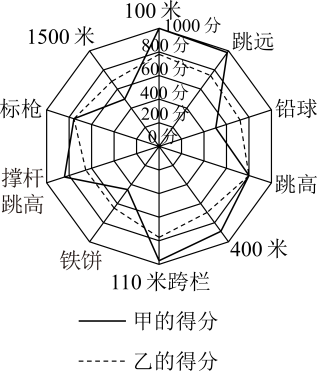 A、在米跑项目中,甲的得分比乙的得分低 B、在跳高和标枪项目中,甲、乙水平相当 C、甲的各项得分比乙的各项得分更均衡 D、甲的各项得分的极差比乙的各项得分的极差大11. 古希腊数学家普洛克拉斯指出:“哪里有数,哪里就有美.”“对称美”是数学美的重要组成部分,在数学史上,人类对数学的对称问题一直在思考和探索,图形中对称性的本质就是点的对称、线的对称.如正方形既是轴对称图形,又是中心对称图形,对称性也是函数一个非常重要的性质.如果一个函数的图象经过某个正方形的中心并且能够将它的周长和面积同时平分,那么称这个函数为这个正方形的“优美函数”.下列关于“优美函数”的说法中正确的有( )A、函数可以是某个正方形的“优美函数” B、函数只能是边长不超过的正方形的“优美函数” C、函数可以是无数个正方形的“优美函数” D、若函数是“优美函数”,则的图象一定是中心对称图形12. 已知正数x,y满足 , 则下列结论正确的是( )A、 B、 C、 D、
A、在米跑项目中,甲的得分比乙的得分低 B、在跳高和标枪项目中,甲、乙水平相当 C、甲的各项得分比乙的各项得分更均衡 D、甲的各项得分的极差比乙的各项得分的极差大11. 古希腊数学家普洛克拉斯指出:“哪里有数,哪里就有美.”“对称美”是数学美的重要组成部分,在数学史上,人类对数学的对称问题一直在思考和探索,图形中对称性的本质就是点的对称、线的对称.如正方形既是轴对称图形,又是中心对称图形,对称性也是函数一个非常重要的性质.如果一个函数的图象经过某个正方形的中心并且能够将它的周长和面积同时平分,那么称这个函数为这个正方形的“优美函数”.下列关于“优美函数”的说法中正确的有( )A、函数可以是某个正方形的“优美函数” B、函数只能是边长不超过的正方形的“优美函数” C、函数可以是无数个正方形的“优美函数” D、若函数是“优美函数”,则的图象一定是中心对称图形12. 已知正数x,y满足 , 则下列结论正确的是( )A、 B、 C、 D、三、填空题
-
13. 已知向量 , , 且 , 则 .14. 设E,F分别在正方体的棱 , 上,且 , , 则直线与所成角的余弦值为.15. 已知抛物线的焦点为F,过F且被C截得的弦长为4的直线有且仅有两条,写出一个满足条件的抛物线C的方程: , 此时该弦的中点到x轴的距离为.16. 对20不断进行“乘以2”或“减去3”的运算,每进行一次记为一次运算,若运算次得到的结果为23,则的最小值为.
四、解答题
-
17. 已知等差数列满足 , , 公比不为的等比数列满足 , .(1)、求与通项公式;(2)、设 , 求的前n项和.18. 2023年,全国政协十四届一次会议于3月4日下午3时在人民大会堂开幕,3月11日下午闭幕,会期7天半;十四届全国人大一次会议于3月5日上午开幕,13日上午闭幕,会期8天半.为调查学生对两会相关知识的了解情况,某高中学校开展了两会知识问答活动,现从全校参与该活动的学生中随机抽取320名学生,他们的得分(满分100分)的频率分布折线图如下.

参考数据: , , , , .
(1)、若此次知识问答的得分 , 用样本来估计总体,设 , 分别为被抽取的320名学生得分的平均数和标准差,求的值;(2)、学校对这些被抽取的320名学生进行奖励,奖励方案如下:用频率估计概率,得分小于或等于55的学生获得1次抽奖机会,得分高于55的学生获得2次抽奖机会.假定每次抽奖抽到价值10元的学习用品的概率为 , 抽到价值20元的学习用品的概率为.从这320名学生中任取一位,记该同学在抽奖活动中获得学习用品的价值总额为元,求的分布列和数学期望(用分数表示),并估算此次抽奖要准备的学习用品的价值总额.19. 在四棱锥中,四边形为等腰梯形, , , , .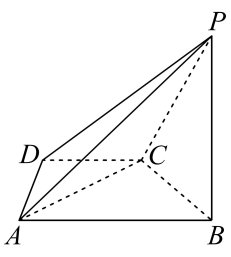 (1)、证明:平面平面;(2)、若 , , 求直线与平面所成角的正弦值.
(1)、证明:平面平面;(2)、若 , , 求直线与平面所成角的正弦值.