河南省洛阳市2022-2023学年高二下学期理数期中考试试卷
试卷更新日期:2023-04-28 类型:期中考试
一、单选题
-
1. 某直线运动的物体从时刻到的位移为 , 那么为( )A、从时刻到物体的平均速度 B、从时刻到位移的平均变化率 C、当时刻为时该物体的速度 D、该物体在时刻的瞬时速度2. 假设某地在20年间的年均通货膨胀率为5%,物价(单位:元)与时间(单位:年)之间的关系为 , 其中为时的物价.假定某种商品的 , 那么在第10个年头,这种商品的价格上涨的速度大约为(精确到0.001元/年)( )
附: , , .
A、0.079元/年 B、0.076元/年 C、1.629元/年 D、1.551元/年3. 小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )A、 B、
B、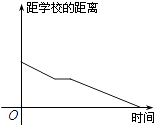 C、
C、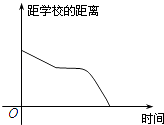 D、
D、 4. 曲线在点处的切线垂直于直线 , 则( )A、1 B、-1 C、 D、5. 的展开式的第6项的系数是( )A、 B、 C、 D、6. 6名同学排成一排,其中甲、乙、丙三人必须在一起的不同排法共有( )A、36种 B、72种 C、144种 D、720种7. 已知函数在时有极大值,则的极大值为( )A、0 B、32 C、0或32 D、0或-328. 的展开式中各项系数的和为2,则该展开式中常数项为( )
4. 曲线在点处的切线垂直于直线 , 则( )A、1 B、-1 C、 D、5. 的展开式的第6项的系数是( )A、 B、 C、 D、6. 6名同学排成一排,其中甲、乙、丙三人必须在一起的不同排法共有( )A、36种 B、72种 C、144种 D、720种7. 已知函数在时有极大值,则的极大值为( )A、0 B、32 C、0或32 D、0或-328. 的展开式中各项系数的和为2,则该展开式中常数项为( )
A、-40 B、-20 C、20 D、409. 函数的单调递增区间为( )A、 B、 C、 D、10. 将6名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行服务,每名志原者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )A、480种 B、1080种 C、1560种 D、2640种11. 已知函数在时有极值0,则( )A、4 B、11 C、4或11 D、以上答案都不对12. 设函数(其中为自然对数的底数),若函数至少存在一个零点,则实数的取值范围是A、 B、 C、 D、二、填空题
-
13. 如图,从甲地到乙地有2条路,从乙地到丁地有4条路;从甲地到丙地有4条路,从丙地到丁地有2条路.则从甲地到丁地共有条不同的路.
 14. 已知 , , , 且 , , , 其中是自然对数的底数,则实数 , , 的大小关系是.(用“<”连接)15. 甲、乙、丙、丁、戊5名学生进行某种劳动技能比赛,决出第1名到第5名的名次.甲、乙两名参赛者去询问成绩,回答者对甲说:“很遗憾,你和乙都未拿到冠军”,对乙说:“你当然不会是最差的”,从这个回答分析,5人的名次排列共可能有种不同的情况.(用数字作答)16. 已知函数 , 若在定义域上单调递增,则实数的取值范围是 .
14. 已知 , , , 且 , , , 其中是自然对数的底数,则实数 , , 的大小关系是.(用“<”连接)15. 甲、乙、丙、丁、戊5名学生进行某种劳动技能比赛,决出第1名到第5名的名次.甲、乙两名参赛者去询问成绩,回答者对甲说:“很遗憾,你和乙都未拿到冠军”,对乙说:“你当然不会是最差的”,从这个回答分析,5人的名次排列共可能有种不同的情况.(用数字作答)16. 已知函数 , 若在定义域上单调递增,则实数的取值范围是 .三、解答题
-
17. 已知函数 .(1)、求曲线 在点 处的切线方程;(2)、求函数 在区间 上的最大值和最小值.18. 某医院呼吸内科有3名男医生、2名女医生,其中李亮(男)为科室主任;感染科有2名男医生、2名女医生,其中张雅(女)为科室主任.现在院方决定从两科室中选4人参加培训.(1)、若至多有1名主任参加,则有多少种派法?(2)、若呼吸内科至少有2名医生参加,则有多少种派法?(3)、若至少有1名主任参加,且有女医生参加,则有多少种派法?19. 已知二次函数 , 其导函数的图象如图, .
 (1)、求函数的解析式;(2)、若函数在区间上是单调函数,求实数的取值范围.
(1)、求函数的解析式;(2)、若函数在区间上是单调函数,求实数的取值范围.