河北省承德市重点高中2022-2023学年高一下学期数学期中联考试卷
试卷更新日期:2023-04-28 类型:期中考试
一、单选题
-
1. 已知复数满足 , 则的虚部为( )A、-2 B、-1 C、 D、22. 下列说法中不正确的是( )A、零向量与任一向量平行 B、方向相反的两个非零向量不一定共线 C、单位向量是模为1的向量 D、方向相反的两个非零向量必不相等3. 在中,若 , 则( )A、 B、16 C、9 D、04. 若 , , 则的值为( )A、 B、 C、 D、5. 在中,角所对的边分别为 , 若 , , , 则此三角形解的情况为( )A、无解 B、有两解 C、有一解 D、有无数解6. 已知的三边长分别为 , , , 且最大内角是最小内角的2倍,则最小内角的余弦值为( )A、 B、 C、 D、7. 已知点是所在平面内一点,若非零向量与向量共线,则( )A、 B、 C、 D、8. 将函数的图象向右平移个单位长度后得到的图象,若在上单调递增,则的取值范围为( )A、 B、 C、 D、
二、多选题
-
9. 若复数为纯虚数,则( )A、为实数 B、为实数 C、为实数 D、为实数10. 已知函数 , 则下列关于函数的图象与性质的叙述中,正确的有( )A、函数的最小正周期为 B、函数在上单调递增 C、函数的图象关于直线对称 D、11. 已知非零向量 , 满足 , 则下列结论正确的是( )A、若 , 共线,则 B、若 , 则 C、若 , 则 D、12. 在锐角中,内角A,B,C的对边分别为a,b,c, , 且 , 则下列结论正确的是( )A、 B、a>c C、c>a D、
三、填空题
-
13. 计算:.14. 已知 , 向量在上的投影向量为 , 则.15. 已知某扇形材料的面积为 , 圆心角为 , 则用此材料切割出的面积最大的圆的周长为.16. 记的内角 , , 的对边分别为 , , , 若为的重心, , , 则 .
四、解答题
-
17. 已知虚数z满足.(1)、求证:在复平面内对应的点在直线上;(2)、若是方程的一个根,求与.18. 已知函数的图象的一部分如图所示.
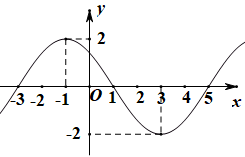 (1)、求函数的解析式;(2)、当时,求函数的最值.19. 已知的内角的对边分别为 , 向量 , 且.(1)、求角A;(2)、若的周长为 , 且外接圆的半径为1,判断的形状,并求的面积.20. 已知向量 , 满足 , , .(1)、求向量与的夹角;(2)、求 .21. 2023年的春节,人们积蓄已久的出行热情似乎在这一刻被引爆,让旅游业终于迎来真正意义上的“触底反弹”.如图是某旅游景区中的网红景点的路线图,景点A处下山至处有两种路径:一种是从A沿直线步行到 , 另一种是先从A沿索道乘缆车到B,然后从B 沿直线步行到.现有甲、乙两位游客从A处下山,甲沿匀速步行,速度为.在甲出发后,乙从A乘缆车到B ,在B 处停留后,再从B 匀速步行到.假设缆车匀速直线运行的速度为 , 索道长为 , 经测量,.
(1)、求函数的解析式;(2)、当时,求函数的最值.19. 已知的内角的对边分别为 , 向量 , 且.(1)、求角A;(2)、若的周长为 , 且外接圆的半径为1,判断的形状,并求的面积.20. 已知向量 , 满足 , , .(1)、求向量与的夹角;(2)、求 .21. 2023年的春节,人们积蓄已久的出行热情似乎在这一刻被引爆,让旅游业终于迎来真正意义上的“触底反弹”.如图是某旅游景区中的网红景点的路线图,景点A处下山至处有两种路径:一种是从A沿直线步行到 , 另一种是先从A沿索道乘缆车到B,然后从B 沿直线步行到.现有甲、乙两位游客从A处下山,甲沿匀速步行,速度为.在甲出发后,乙从A乘缆车到B ,在B 处停留后,再从B 匀速步行到.假设缆车匀速直线运行的速度为 , 索道长为 , 经测量,.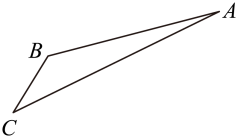 (1)、求山路的长;(2)、乙出发多少分钟后,乙在缆车上与甲的距离最短?22. 已知圆的半径为2,圆与正的各边相切,动点在圆上,点满足.(1)、求的值;(2)、若存在 , 使得 , 求的最大值.
(1)、求山路的长;(2)、乙出发多少分钟后,乙在缆车上与甲的距离最短?22. 已知圆的半径为2,圆与正的各边相切,动点在圆上,点满足.(1)、求的值;(2)、若存在 , 使得 , 求的最大值.