人教版初中数学几何辅助线进阶训练——一般四边形的辅助线:连对角线、延长对边、作平行
试卷更新日期:2023-04-28 类型:复习试卷
一、阶段一(较易)
-
1. 如图,在四边形 中, , , , , ,求 的长.
 2. 如图,在四边形ABCD中,已知∠B=90°,AB=4,BC=3,CD=12,AD=13,求四边形ABCD的面积.
2. 如图,在四边形ABCD中,已知∠B=90°,AB=4,BC=3,CD=12,AD=13,求四边形ABCD的面积. 3. 如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA= , 求四边形ABCD的面积.
3. 如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA= , 求四边形ABCD的面积. 4. 如图,四边形 是我县某校在校园一角开辟的一块四边形的“试验田”,经过测量得知 .求四边形 的面积.
4. 如图,四边形 是我县某校在校园一角开辟的一块四边形的“试验田”,经过测量得知 .求四边形 的面积. 5. 已如:如图,四边形中, , 求四边形的面积.
5. 已如:如图,四边形中, , 求四边形的面积. 6. 如图,在四边形ABCD中,AD= , AB=5,BC=10,CD=8,∠BAD=90°,求四边形ABCD的面积.
6. 如图,在四边形ABCD中,AD= , AB=5,BC=10,CD=8,∠BAD=90°,求四边形ABCD的面积.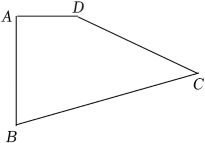 7. 如图,在四边形ABCD中, . 求:四边形ABCD的面积.
7. 如图,在四边形ABCD中, . 求:四边形ABCD的面积. 8. 已知:如图,四边形ABCD中,AB=BC=2,CD=1,DA=3,∠ABC=90°,求四边形ABCD的面积.
8. 已知:如图,四边形ABCD中,AB=BC=2,CD=1,DA=3,∠ABC=90°,求四边形ABCD的面积. 9. 如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.
9. 如图,在四边形ABCD中,AD=4,BC=1,∠A=30°,∠B=90°,∠ADC=120°,求CD的长.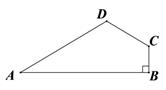 10. 如图,四边形 中, , , , ,求 的度数.
10. 如图,四边形 中, , , , ,求 的度数.
二、阶段二(中等)
-
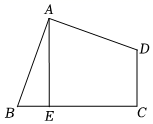
11. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC,垂足为E,AE=3,求四边形ABCD的面积.
 12. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.
12. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.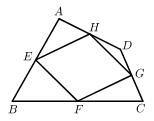 13. 如图所示,四边形ABCD,已知AB⊥BC,AB⊥AD,AB=BC=2,CD . 计算这个四边形的面积.
13. 如图所示,四边形ABCD,已知AB⊥BC,AB⊥AD,AB=BC=2,CD . 计算这个四边形的面积. 14. 如图,在四边形中, , 求的长.
14. 如图,在四边形中, , 求的长. 15. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .
15. 如图,四边形 中, , , ,M、N分别为AB、AD上的动点,且 .求证: .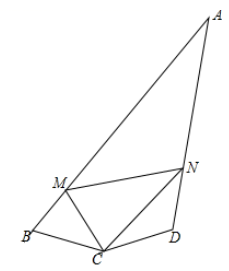 16. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD , AE⊥BC于E , 若线段AE=5,BE=2,则S四边形ABCD的面积为多少?
16. 如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD , AE⊥BC于E , 若线段AE=5,BE=2,则S四边形ABCD的面积为多少? 17. 有一块如图所示的四边形空地,求此空地的面积.(结果保留根号)
17. 有一块如图所示的四边形空地,求此空地的面积.(结果保留根号) 18. 四边形 中, , 平分 , , , ,求 的长.
18. 四边形 中, , 平分 , , , ,求 的长. 19. 如图,四边形ABCD是一个菱形绿地,其周长为40 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数)
19. 如图,四边形ABCD是一个菱形绿地,其周长为40 m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2 , 请问需投资金多少元?(结果保留整数) 20. 如图,在四边形 中, , .求证: .
20. 如图,在四边形 中, , .求证: .
三、阶段三(较难)
-
21. 如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
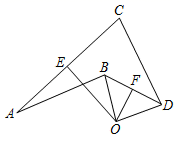 22. 如图,在四边形 中, 、 是对角线,已知 是等边三角形, , , ,求边 的长.
22. 如图,在四边形 中, 、 是对角线,已知 是等边三角形, , , ,求边 的长. 23.
23.如图1,在平面直角坐标系中,四边形OABC各顶点的坐标分别O(0,0),A(3,3 ),B(9,5 ),C(14,0).动点P与Q同时从O点出发,运动时间为t秒,点P沿OC方向以1单位长度/秒的速度向点C运动,点Q沿折线OA−AB−BC运动,在OA,AB,BC上运动的速度分别为3, , (单位长度/秒)﹒当P,Q中的一点到达C点时,两点同时停止运动.

 (1)、求AB所在直线的函数表达式.(2)、如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.(3)、在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.24.
(1)、求AB所在直线的函数表达式.(2)、如图2,当点Q在AB上运动时,求△CPQ的面积S关于t的函数表达式及S的最大值.(3)、在P,Q的运动过程中,若线段PQ的垂直平分线经过四边形OABC的顶点,求相应的t值.24.四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
 25. 如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD= ,BC=4 ,求CD的长.
25. 如图,在梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AD= ,BC=4 ,求CD的长. 26. 如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2 ,求PB+PE的最小值是多少?
26. 如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2 ,求PB+PE的最小值是多少? 27. 公园里有一块形如四边形ABCD的草地,测得BC=CD=20米,∠A=45°,∠B=∠C=120°,请求出这块草地面积.
27. 公园里有一块形如四边形ABCD的草地,测得BC=CD=20米,∠A=45°,∠B=∠C=120°,请求出这块草地面积. 28. 如图:
28. 如图:
【问题背景】
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,点E、F分别是边BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使GD=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ▲ .
【探索延伸】
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,点E、F分别是边BC、CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由.

