天津市东丽区2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 估计×+的运算结果应在( )A、6到7之间 B、7到8之间 C、8到9之间 D、9到10之间2. 已知 , , 则代数式的值是( )A、 B、 C、24 D、3. 如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )A、1,2,3 B、1,1, C、1,1, D、1,2,4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形5. 如图,菱形ABCD中, ,则 ( )
 A、30° B、25° C、20° D、15°6. 如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化,下列从图象中得到的信息正确的是( )
A、30° B、25° C、20° D、15°6. 如图是自动测温仪记录的图象,它反映了齐齐哈尔市的春季某天气温T如何随时间t的变化而变化,下列从图象中得到的信息正确的是( )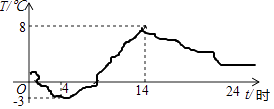 A、0点时气温达到最低 B、最低气温是零下4℃ C、0点到14点之间气温持续上升 D、最高气温是8℃7. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中 , 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( )
A、0点时气温达到最低 B、最低气温是零下4℃ C、0点到14点之间气温持续上升 D、最高气温是8℃7. 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中 , 分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象,以下说法:①甲比乙提前12分到达;②甲的平均速度为15千米/时;③甲乙相遇时,乙走了6千米;④乙出发6分钟后追上甲.其中正确的有( ) A、4个 B、3个 C、2个 D、1个8. 歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,肯定不会对所有评委打分的哪一个统计量产生影响( )A、平均分 B、众数 C、中位数 D、极差9. 如图,在矩形中, , , 平分 , 分别过点B、C作于点E,于点F,则的值为( )
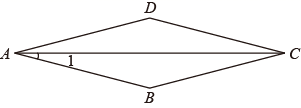
A、4个 B、3个 C、2个 D、1个8. 歌唱比赛有二十位评委给选手打分,统计每位选手得分时,会去掉一个最高分和一个最低分,这样做,肯定不会对所有评委打分的哪一个统计量产生影响( )A、平均分 B、众数 C、中位数 D、极差9. 如图,在矩形中, , , 平分 , 分别过点B、C作于点E,于点F,则的值为( ) A、1 B、 C、 D、10. 如图,菱形 的边长是4厘米, ,动点 以1厘米/秒的速度自 点出发沿 方向运动至 点停止,动点 以2厘米/秒的速度自 点出发沿折线 运动至 点停止若点 同时出发运动了 秒,记 的面积为 ,下面图象中能表示 与 之间的函数关系的是( )
A、1 B、 C、 D、10. 如图,菱形 的边长是4厘米, ,动点 以1厘米/秒的速度自 点出发沿 方向运动至 点停止,动点 以2厘米/秒的速度自 点出发沿折线 运动至 点停止若点 同时出发运动了 秒,记 的面积为 ,下面图象中能表示 与 之间的函数关系的是( ) A、
A、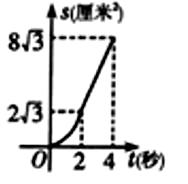 B、
B、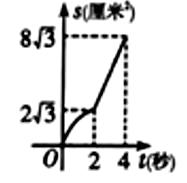 C、
C、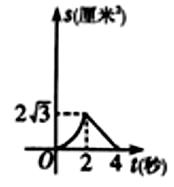 D、
D、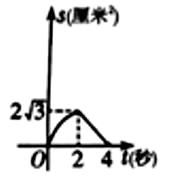
二、填空题
-
11. 如图,在等腰中, , , 以为直角边作等腰△ , 以为直角边作等腰△ , 则的长度为 .
 12. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:
12. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:①△EBF≌△DFC;
②四边形AEFD为平行四边形;
③当AB=AC,∠BAC=1200时,四边形AEFD是正方形.
其中正确的结论是 . (请写出正确结论的番号).

三、解答题
-
13. 计算:.14. 若a、b、c为△ABC的三边长,且a、b、c满足等式 ,求△ABC的面积.15. 如图,直角坐标系xOy中,一次函数y=﹣ x+5的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,4).
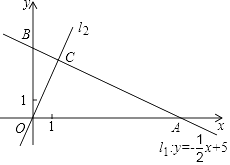 (1)、求m的值及l2的解析式;
(1)、求m的值及l2的解析式;
(2)、求S△AOC﹣S△BOC的值;(3)、一次函数y=kx+1的图象为l3 , 且11 , l2 , l3不能围成三角形,直接写出k的值.
16. 某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍,为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图(不完整)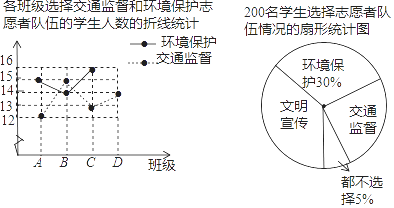 (1)、求扇形统计图中交通监督所在扇形的圆心角度数;
(1)、求扇形统计图中交通监督所在扇形的圆心角度数;
(2)、求D班选择环境保护的学生人数,并补全折线统计图;(温馨提示:请画在答题卷相对应的图上)
(3)、若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
17. 如图所示,在矩形中, , , 将矩形沿折叠后,点D落在点 E处,且与交于F. (1)、判断的形状,并说明理由.(2)、求的面积.18. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后小时血液中含药量最高,达每毫升微克,接着逐步衰减,小时时血液中含药量为每毫升微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后,
(1)、判断的形状,并说明理由.(2)、求的面积.18. 某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后小时血液中含药量最高,达每毫升微克,接着逐步衰减,小时时血液中含药量为每毫升微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示,当成人按规定剂量服药后, (1)、求y与x之间的解析式;(2)、如果每毫升血液中含药量不低于5微克时,在治疗疾病时是有效的,那么该药的有效时间是多少?.19. 如图1,已知直线y=2x+2与y轴,x轴分别交于A,B两点,以B为直角顶点在第二象限作等腰Rt△ABC
(1)、求y与x之间的解析式;(2)、如果每毫升血液中含药量不低于5微克时,在治疗疾病时是有效的,那么该药的有效时间是多少?.19. 如图1,已知直线y=2x+2与y轴,x轴分别交于A,B两点,以B为直角顶点在第二象限作等腰Rt△ABC (1)、求点C的坐标,并求出直线AC的关系式;(2)、如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)、如图3,在(1)的条件下,直线AC交x轴于点M,P(- , k)是线段BC上一点,在x轴上是否存在一点N,使△BPN面积等于△BCM面积的一半?若存在,请求出点N的坐标;若不存在,请说明理由.20. 如图,在平面直角坐标系中,点A(0,3),B( , 0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)、求点C的坐标,并求出直线AC的关系式;(2)、如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)、如图3,在(1)的条件下,直线AC交x轴于点M,P(- , k)是线段BC上一点,在x轴上是否存在一点N,使△BPN面积等于△BCM面积的一半?若存在,请求出点N的坐标;若不存在,请说明理由.20. 如图,在平面直角坐标系中,点A(0,3),B( , 0),AB =6,作∠DBO=∠ABO,点H为y轴上的点,∠CAH=∠BAO,BD交y轴于点E,直线DO交AC于点C.
 (1)、证明:△ABE为等边三角形;(2)、若CD⊥AB于点F,求线段CD的长;(3)、动点P从A出发,沿A-O-B路线运动,速度为1个单位长度每秒,到B点处停止运动;动点Q从B出发,沿B-O-A路线运动,速度为2个单位长度每秒,到A点处停止运动.两点同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间时△OPM与△OQN全等?
(1)、证明:△ABE为等边三角形;(2)、若CD⊥AB于点F,求线段CD的长;(3)、动点P从A出发,沿A-O-B路线运动,速度为1个单位长度每秒,到B点处停止运动;动点Q从B出发,沿B-O-A路线运动,速度为2个单位长度每秒,到A点处停止运动.两点同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间时△OPM与△OQN全等?