山西省吕梁市孝义市2021-2022学年八年级下学期期末数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 下列是最简二次根式的是( )A、 B、 C、 D、2. 在学校的体育训练中,李明投掷实心球的7次成绩如下表所示,则这7次成绩的中位数是( )
次数
1
2
3
4
5
6
7
成绩/米
9.7
9.6
9.8
10
9.8
9.9
10.1
A、9.6米 B、9.7米 C、9.8米 D、9.9米3. 下列长度的线段中,能组成直角三角形的一组是( )A、1, , 2 B、2,3,4 C、4,5,6 D、5,6,74. 爷爷在离家900米的公园锻炼后回家,离开公园20分钟后,爷爷停下来与朋友聊天10分钟,接着又走了15分钟回到家中.下面图形中表示爷爷离家的距离y(米)与爷爷离开公园的时间x(分)之间的函数关系是( )A、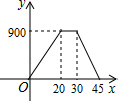 B、
B、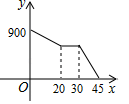 C、
C、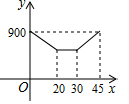 D、
D、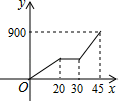 5. 某品牌鞋店一周内销售了某款男鞋60双,各种尺码鞋的销量如下面统计图所示,则这周卖出的鞋的尺码组成的一组数据的众数为( )
5. 某品牌鞋店一周内销售了某款男鞋60双,各种尺码鞋的销量如下面统计图所示,则这周卖出的鞋的尺码组成的一组数据的众数为( )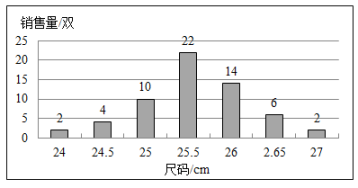 A、22cm B、25.5cm C、26cm D、27cm6. 如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标介于( )
A、22cm B、25.5cm C、26cm D、27cm6. 如图,在平面直角坐标系中,已知点A(﹣2,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的正半轴于点C,则点C的横坐标介于( )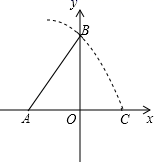 A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间7. 如图,在中,对角线AC、BD相交于点O,交AD于点E,连接BE,若的周长为42,则的周长为( )
A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间7. 如图,在中,对角线AC、BD相交于点O,交AD于点E,连接BE,若的周长为42,则的周长为( ) A、32 B、28 C、24 D、218. 如图,从一个大正方形中裁去面积为6cm2和15cm2的两个小正方形,则留下阴影部分的面积为( )
A、32 B、28 C、24 D、218. 如图,从一个大正方形中裁去面积为6cm2和15cm2的两个小正方形,则留下阴影部分的面积为( ) A、 B、 C、 D、9. 如图,点E在正方形ABCD的边BC上,若 , , 则AD的长度为( )
A、 B、 C、 D、9. 如图,点E在正方形ABCD的边BC上,若 , , 则AD的长度为( )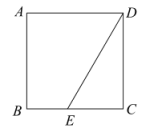 A、 B、 C、3 D、510. 一次函数与(a,b为常数,且),在同一直角坐标系中的图像可能是( )A、
A、 B、 C、3 D、510. 一次函数与(a,b为常数,且),在同一直角坐标系中的图像可能是( )A、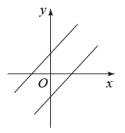 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 二次根式 在实数范围内有意义,x的取值范围是.12. 如图是甲、乙两名同学的8次射击训练成绩的折线统计图,他们的平均成绩相同,若要从这两位同学中选一名成绩较为稳定的同学参加学校运动会的射击项目,则应选 .
 13. 如图,直线与直线交于点 , 则方程的解为 .
13. 如图,直线与直线交于点 , 则方程的解为 . 14. 图,在中, , 是边上的中线,若 , , 则.
14. 图,在中, , 是边上的中线,若 , , 则. ,15. 如图,在菱形ABCD中, , 点E为对角线AC上一点,且 , 连接DE,若 , 则DE的长为 .
,15. 如图,在菱形ABCD中, , 点E为对角线AC上一点,且 , 连接DE,若 , 则DE的长为 .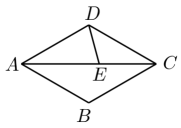
三、解答题
-
16. 计算(1)、(2)、17. 2022年5月30日是第六个全国科技工作者日,主题为“创新争先,自立自强”.为了庆祝第六个全国科技工作者日,学校举办科技知识竞赛活动,竞赛内容分“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目,下表是小亮和小明的各项成绩:(百分制)
航天技术
生物技术
能源技术
其它技术领域
小亮
85
90
95
90
小明
100
90
80
90
若“航天技术”,“生物技术”,“能源技术”,“其它技术领域”四个项目按确定综合成绩,则小亮和小明谁的综合成绩高?请通过计算说明理由.
18. 如图1是吊车的实物图,图2是吊车工作示意图.吊车作业时是通过液压杆CD的伸缩使起重臂AB绕点B转动的,从而使得起重臂升降作业(起重臂AB的长度也可以伸缩)在某次起重作业中,学习兴趣小组测经过测量和咨询工人师傅了解到如下信息:如图3,起重臂米,点B到地面的距离米,钢丝绳所在直线AF垂直地面于点F,点B到AF的距离米.求点A到地面的距离AF的长为多少米? 19. 炎热的夏天,西瓜深受人们的青睐.某超市批发A,B两种西瓜共600千克进行销售,售价与进价如下表所示:
19. 炎热的夏天,西瓜深受人们的青睐.某超市批发A,B两种西瓜共600千克进行销售,售价与进价如下表所示:名称
A种西瓜
B种西瓜
进价(元/千克)
4
3
售价(元/千克)
6
4
设A种西瓜批发x千克,全部售完后总利润为y元.
(1)、求y与x的函数关系式;(2)、若购进A种西瓜不少于B种西瓜的2倍.求这批西瓜全部售出后最小利润是多少元?20. 阅读下列材料,并完成相应任务.运用“双求法”证明勾股定理勾股定理表现了我国古人对数学的钻研精神和聪明才智,是我国古代数学的骄傲,它神秘而美妙,证法多样,是数学定理中证明方法最多的定理之一.勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.数学上把这种方法称之为“双求法”.
下面是利用“双求法”证明勾股定理的一种思路:
如图1,将两个全等的直角三角形与如图摆放,其中 , , , . 连接BD,过点D作BC延长线的垂线,垂足为F,容易得出 , 用含a,b,c的式子表示出上面四个三角形的面积,就能完成勾股定理的证明.
 (1)、任务一:请你根据上述材料中的思路证明勾股定理;(2)、任务二:请你用“双求法”解决下列问题;
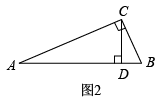
(1)、任务一:请你根据上述材料中的思路证明勾股定理;(2)、任务二:请你用“双求法”解决下列问题;如图2,中, , CD是AB边上的高,若 , , 则 . (直接写出答案)
 21. 综合与实践
21. 综合与实践问题情境:学习完平行四边形的性质和判定后,老师创设了如下探究情境,探究三角形的中位线定理.
问题1:如图1,在中,对角线AC,BD相交于点O,E为AB上一点,连接EO并延长交CD于F,则OE与OF有怎样的数量关系?

小明: .
理由如下:∵四边形ABCD是平行四边形,
∴ , (依据1)
∴
又∵ ,
∴(依据2).
∴
问题2:如图2,若点E为AB的中点,其他条件不变,则线段EF与BC有怎样的数量关系和位置关系?
小亮: , BC.
理由如下:….
问题3:如图3,在中,D,E分别是AB,AC的中点,连接DE,像DE这样,连接三角形两边中点的线段叫做三角形的中位线.通过前面问题给你的启发,你能猜想出DE和BC的数量关系和位置关系吗?
小慧:BC, .
…
数学思考:
(1)、请你写出小明推理过程中的“依据1”和“依据2”:依据1:;依据2: .
(2)、请你帮助小亮写出问题2的证明过程.(温馨提示:不能用三角形的中位线定理证明哦!)(3)、问题解决:请用图3写出三角形中位线定理的证明过程.
22. 综合与探究.如图,一次函数的图像与坐标轴交于A,B两点,点C的坐标为 , 点D是直线BC上一动点,点D的横坐标为m.
 (1)、直接写出点A,B的坐标及直线BC的解析式;(2)、当点D在线段BC上时,设的面积为S.
(1)、直接写出点A,B的坐标及直线BC的解析式;(2)、当点D在线段BC上时,设的面积为S.①请用含m的式子表示出S;
②当的面积等于面积的时,求出m的值;
(3)、在y轴上是否存在一点E,使以点A,B,D,E为顶点的四边形是平行四边形,若存在,直接写出点E的坐标,若不存在,说明理由.