山西省晋城市高平市2021-2022学年八年级下学期期末质量监测数学试卷
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 若分式有意义,则( )A、 B、 C、 D、2. 如图所示,四边形 是平行四边形,点 在线段 的延长线上,若 ,则 ( )
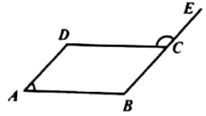 A、 B、 C、 D、3. 已知点 , 在一次函数的图象上,则m与n的大小关系是( )A、 B、 C、 D、无法确定4. 如图,在菱形 中,对角线 ,则 的面积为( )
A、 B、 C、 D、3. 已知点 , 在一次函数的图象上,则m与n的大小关系是( )A、 B、 C、 D、无法确定4. 如图,在菱形 中,对角线 ,则 的面积为( )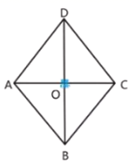 A、9 B、10 C、11 D、125. 已知反比例函数 , 则下列描述错误的是( )A、图象位于第一,第三象限 B、图像必经过点 C、图象不可能与坐标轴相交 D、y随x的增大而减小6. 下面是一位同学做分式运算的过程,M,N代表代数式,则下列关于M、N的式子正确的是( )A、 B、 C、 D、7. 如图,在平行四边形中,的平分线交于点E,的平分线交于点F,若 , , 则的长是( )
A、9 B、10 C、11 D、125. 已知反比例函数 , 则下列描述错误的是( )A、图象位于第一,第三象限 B、图像必经过点 C、图象不可能与坐标轴相交 D、y随x的增大而减小6. 下面是一位同学做分式运算的过程,M,N代表代数式,则下列关于M、N的式子正确的是( )A、 B、 C、 D、7. 如图,在平行四边形中,的平分线交于点E,的平分线交于点F,若 , , 则的长是( ) A、2 B、1 C、3 D、3.58. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、
A、2 B、1 C、3 D、3.58. 新龟兔赛跑的故事:龟兔从同一地点同时出发后,兔子很快把乌龟远远甩在后头.骄傲自满的兔子觉得自己遥遥领先,就躺在路边呼呼大睡起来.当它一觉醒来,发现乌龟已经超过它,于是奋力直追,最后同时到达终点.用S1、S2分别表示乌龟和兔子赛跑的路程,t为赛跑时间,则下列图象中与故事情节相吻合的是( )A、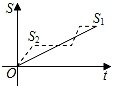 B、
B、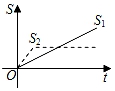 C、
C、 D、
D、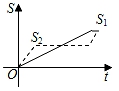 9. 为了考察甲、乙两块地中小麦的长势,分别从中随机抽出10株麦苗,测得麦苗高如图所示,若和分别表示甲、乙两块地麦苗高数据的方差,则( )
9. 为了考察甲、乙两块地中小麦的长势,分别从中随机抽出10株麦苗,测得麦苗高如图所示,若和分别表示甲、乙两块地麦苗高数据的方差,则( ) A、= B、< C、> D、不确定10. 如图,在正方形中,点P在边上,于点E,于点F,若 , , 则( )
A、= B、< C、> D、不确定10. 如图,在正方形中,点P在边上,于点E,于点F,若 , , 则( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 如图是一片枫叶标本,其形状呈“掌状五裂型”,裂片具有少数突出的齿.将其放在平面直角坐标系中,表示叶片“顶部”A,B两点的坐标分别为 , , 则叶杆“底部”点C的坐标为 .
 12. 某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成缋按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取敦师的综合成绩为 .
12. 某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成缋按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,则被录取敦师的综合成绩为 .教师成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分
13. 如图,E是平行四边形内任一点,若 , 则图中阴影部分的面积是 . 14. 如图,点A、C是反比例函数图象上的点,且关于原点对称.过点A作轴于点B,若的面积为7,则反比例函数的表达式为 .
14. 如图,点A、C是反比例函数图象上的点,且关于原点对称.过点A作轴于点B,若的面积为7,则反比例函数的表达式为 . 15. 若点E是的中点, , 将正方形沿折叠,使点D恰好落在边的中点E处,点A的对应点为点P,则折痕的长为 .
15. 若点E是的中点, , 将正方形沿折叠,使点D恰好落在边的中点E处,点A的对应点为点P,则折痕的长为 .
三、解答题
-
16.(1)、计算:(2)、先化简 , 再任意选取x代入求值.
 17. 如图:矩形的对角线相交于点O, , . 求证:四边形是菱形.
17. 如图:矩形的对角线相交于点O, , . 求证:四边形是菱形. 18. 为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息.
18. 为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了部分信息..甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组: ):
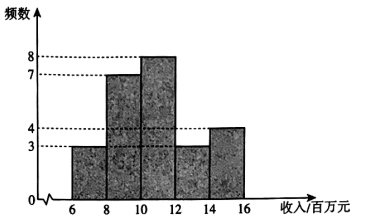
.甲城市邮政企业4月份收入的数据在 这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,11.6,11.8
.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数
中位数
甲城市
10.8
乙城市
11.0
11.5
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .在乙城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .比较 的大小,并说明理由;(3)、若乙城市共有200家邮政企业,估计乙城市的邮政企业4月份的总收入(直接写出结果).19. 1896年,挪威生理学家古德贝发现,每个人有一条腿迈出的步子比另一条腿迈出的步子长的特点,这就导致每个人在蒙上眼晴行走时,虽然主观上沿某一方向直线前进,但实际上走出的是一个大圆圈,这就是有趣的“瞎转圈”现象. 经研究,某人蒙上眼睛走出的大圆圈的半径y(米)是其两腿迈出的步长之差x(厘米)的反比例函数 , 其图象如图所示,请根据图象中的信息解决下列问题: (1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.25厘米时,他蒙上眼睛走出的大圆圈的半径为米;(3)、若某人蒙上眼睛走出的大圆圈的半径不小于70米,则其两腿迈出的步长之差最多是厘米.20. 高平素有梨乡之称,高平大黄梨的甘酸适度,维生素、矿物质含量高,以黄梨为原料制成的梨干因食用方便更是受到了人们的青睐. 某超市欲购进A、B两种袋装黄梨干,用160元购进的A种黄梨干与用240元购进的B种黄梨干的数量相同,每袋B种黄梨干的进价比A种黄梨干的进价贵10元.(1)、求A、B两种黄梨干每袋的进价分别为多少元?(2)、若该商店A种黄梨干每袋售价24元,B种黄梨干每袋售价35元,准备再次购进A,B两种黄梨干共100袋.在这100袋两种黄梨干全部售完的情况下,设购进A种黄梨干的数量为a袋,销售这两种黄梨干的利润为w元,写出w与a的函数关系式,若要保证售完后获利不低于468元,该商店该如何进货?21. 阅读下面材料,完成任务.
(1)、求y与x之间的函数表达式;(2)、当某人两腿迈出的步长之差为0.25厘米时,他蒙上眼睛走出的大圆圈的半径为米;(3)、若某人蒙上眼睛走出的大圆圈的半径不小于70米,则其两腿迈出的步长之差最多是厘米.20. 高平素有梨乡之称,高平大黄梨的甘酸适度,维生素、矿物质含量高,以黄梨为原料制成的梨干因食用方便更是受到了人们的青睐. 某超市欲购进A、B两种袋装黄梨干,用160元购进的A种黄梨干与用240元购进的B种黄梨干的数量相同,每袋B种黄梨干的进价比A种黄梨干的进价贵10元.(1)、求A、B两种黄梨干每袋的进价分别为多少元?(2)、若该商店A种黄梨干每袋售价24元,B种黄梨干每袋售价35元,准备再次购进A,B两种黄梨干共100袋.在这100袋两种黄梨干全部售完的情况下,设购进A种黄梨干的数量为a袋,销售这两种黄梨干的利润为w元,写出w与a的函数关系式,若要保证售完后获利不低于468元,该商店该如何进货?21. 阅读下面材料,完成任务.如图①,在等边三角形内有一点P,且 , , , 求的大小.
李明同学的思路是:将绕点B逆时针旋转 , 画出旋转后的图形(如图②),连接 , 可得是等边三角形,而又是直角三角形(由勾股定理的逆定理可证),所以 , 则 ,

任务:
请你参考李明同学的思路,探究并解决下列问题:如图③,在正方形内有一点P,且 , ,
(1)、求的大小;(2)、求正方形的边长.22. 综合与实践.如图①,四边形是矩形,且 , , O为矩形对角线的交点,E为边上任意一点,连结并延长,与边交于点F. (1)、观察:线段和有什么数量关系?并进行证明.(2)、操作:小英连结、后发现,四边形的形状一定是;当的长为时,四边形是菱形(3)、探究:受小英的启发,小亮对图形进一步操作,将图②中的与分别沿与进行翻折,点A与点C分别落在矩形内的点、处,连结、 , 如图③,请你判断四边形的形状,并证明你的结论.23. 综合与探究:直线与x轴和y轴分别交于点A、B,直线与交于点C,与y轴交于点 , 过点C作轴于点E,点E的横坐标为3.
(1)、观察:线段和有什么数量关系?并进行证明.(2)、操作:小英连结、后发现,四边形的形状一定是;当的长为时,四边形是菱形(3)、探究:受小英的启发,小亮对图形进一步操作,将图②中的与分别沿与进行翻折,点A与点C分别落在矩形内的点、处,连结、 , 如图③,请你判断四边形的形状,并证明你的结论.23. 综合与探究:直线与x轴和y轴分别交于点A、B,直线与交于点C,与y轴交于点 , 过点C作轴于点E,点E的横坐标为3. (1)、求直线的解析式;(2)、点P是x轴上一动点,过点作x轴垂线分别与直线、交于点M、N,求线段的长(用t表示);(3)、在(2)的条件下,t为何值时,以M、N、C、E为顶点的四边形是平行四边形.
(1)、求直线的解析式;(2)、点P是x轴上一动点,过点作x轴垂线分别与直线、交于点M、N,求线段的长(用t表示);(3)、在(2)的条件下,t为何值时,以M、N、C、E为顶点的四边形是平行四边形.