内蒙古自治区乌兰察布市凉城县2021-2022学年八年级下学期期末数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 下列各式中,与是同类二次根式的是( )A、 B、 C、 D、2. 以下列三个数据为三角形的三边,其中能构成直角三角形的是( )A、2,3,4 B、4,5,6 C、5,12,13 D、5,6,73. 下列计算错误的是( )A、 B、 C、 D、4. 某校举行课间操比赛,甲、乙两个班各选出20名学生参加比赛,两个班参赛学生的平均身高都为1.65m,其方差分别是S甲2=3.8,S乙2=3.4,则参赛学生身高比较整齐的班级是( )A、甲班 B、乙班 C、同样整齐 D、无法确定5. 一次函数y=-3x+5的图象不经过的象限是第( )象限A、一 B、二 C、三 D、四6. 在中,如果 , 则的度数是( )A、 B、 C、 D、7. 菱形的两条对角线分别是6cm,8 cm,则菱形面积为( )A、 B、 C、 D、8. 要得到的图象,可把直线向( )A、左平移4个单位 B、右平移4个单位 C、上平移4个单位 D、下平移4个单位9. 下面的性质中,平行四边形、矩形、菱形、正方形都具有的是( )A、四边相等 B、对角线相等 C、对角线互相垂直 D、对角线互相平分10. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是AB的中点,连接EO,若EO = 2,则 CD的长为( )
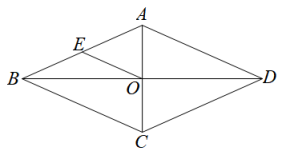 A、2 B、3 C、4 D、511.
A、2 B、3 C、4 D、511.如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路程为x,以点A、P、D为顶点的三角形的面积是y,则下列图象能大致反映y与x的函数关系的是( )
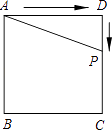 A、
A、 B、
B、 C、
C、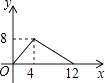 D、
D、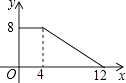 12. 如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论,其中正确的个数有( )
12. 如图,正方形ABCD中,对角线AC、BD交于点O,折叠正方形纸片,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论,其中正确的个数有( )①∠AGD=112.5°;②S△AGD=S△OGD;③四边形AEFG是菱形;④ .
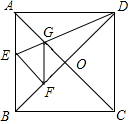 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
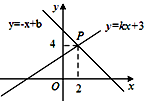
13. 函数y= 的自变量x的取值范围是 .14. , 则x的取值范围是 .15. 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的一元一次不等式kx+3>-x+b的解集是.
 16. 已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是 .17. 如图,从电杆离地面C处向地面拉一条长为8m的钢缆 AC,测得地面AB与钢缆AC的夹角为(),则电线杆C到底部 B的距离为m.
16. 已知一组数据2,1,x,7,3,5,3,2的众数是2,则这组数据的中位数是 .17. 如图,从电杆离地面C处向地面拉一条长为8m的钢缆 AC,测得地面AB与钢缆AC的夹角为(),则电线杆C到底部 B的距离为m.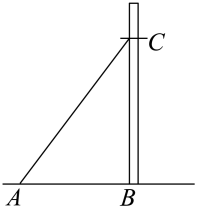 18. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是.
18. 如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是.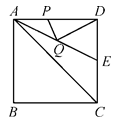
三、解答题
-
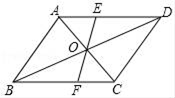
19.(1)、计算(2)、先化简后求值 , 其中20. 已知平行四边形ABCD,对角线AC、BD交于点O,线段EF过点O交AD于点E,交BC于点F.求证:OE=OF.
 21. 中考体育测试前,金川区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
21. 中考体育测试前,金川区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图: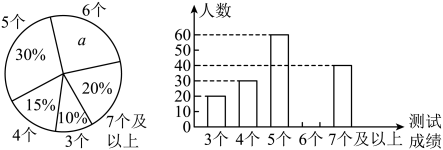
请你根据图中的信息,解答下列问题:
(1)、扇形统计图中a=%,并补全条形统计图.(2)、在这次抽测中,测试成绩的众数和中位数分别是个、个.(3)、该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?22. 已知:如图,正比例函数y=kx的图象经过点A。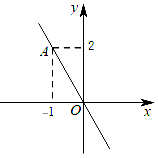 (1)、请你求出该正比例函数的解析式;(2)、若这个函数的图象还经过点B(m,m+3),请你求出m的值;(3)、请你判断点P(﹣ ,1)是否在这个函数的图象上,为什么?23. 如下图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)、请你求出该正比例函数的解析式;(2)、若这个函数的图象还经过点B(m,m+3),请你求出m的值;(3)、请你判断点P(﹣ ,1)是否在这个函数的图象上,为什么?23. 如下图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、点B,点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.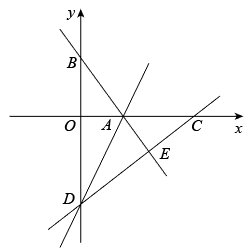 (1)、求AB的长(2)、求点C和点D的坐标(3)、y轴上是否存在一点P,使得?若存在,直接写出点P的坐标;若不存在,请说明理由24. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.
(1)、求AB的长(2)、求点C和点D的坐标(3)、y轴上是否存在一点P,使得?若存在,直接写出点P的坐标;若不存在,请说明理由24. 如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于E,延长BC到点F,使CF=BE,连接DF.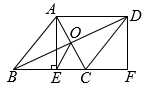 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.25. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AD=10,EC=4,求OE的长度.25. 某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)、该网店甲、乙两种羽毛球每筒的售价各是多少元?(2)、根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?