河北省秦皇岛市卢龙县2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 点P(2,-3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 五边形的外角和等于( ).A、90° B、180° C、360° D、540°3. 刘师傅到加油站加油,如图是所用的加油机上的某一时刻数据显示牌,则其中的变量是( )
 A、金额 B、金额和数量 C、数量 D、单价4. 某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )A、在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测 B、随意调查10名老年人是否参与了新冠病毒核酸和抗体检测 C、在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测 D、利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测5. 如图,在 中, 、 分别是 、 边上的中点,若 ,则 等于( )
A、金额 B、金额和数量 C、数量 D、单价4. 某医疗机构为了了解所在地区老年人参与新冠病毒核酸和抗体检测的比例,分别作出了四种不同的抽样调查,你认为抽样比较合理的是( )A、在公园选择1000名老年人调查是否参与了新冠病毒核酸和抗体检测 B、随意调查10名老年人是否参与了新冠病毒核酸和抗体检测 C、在各医院、卫生院调查1000名老年人是否参与了新冠病毒核酸和抗体检测 D、利用所辖派出所的户籍网随机调查10%老年人是否参与了新冠病毒核酸和抗体检测5. 如图,在 中, 、 分别是 、 边上的中点,若 ,则 等于( ) A、2 B、4 C、8 D、106. 要得到函数y=2x﹣3的图象,只需将函数y=2x的图象( )A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位7. 如图,若棋子“炮”的坐标为 ,棋子“马”的坐标为 ,则棋子“车”的坐标为( )
A、2 B、4 C、8 D、106. 要得到函数y=2x﹣3的图象,只需将函数y=2x的图象( )A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位7. 如图,若棋子“炮”的坐标为 ,棋子“马”的坐标为 ,则棋子“车”的坐标为( ) A、 B、 C、 D、8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )A、
A、 B、 C、 D、8. 已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=﹣kx+k的图象大致是( )A、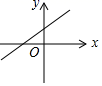 B、
B、 C、
C、 D、
D、 9. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )
9. 如图,▱ABCD中,要在对角线BD上找点E、F,使四边形AECF为平行四边形,现有甲、乙、丙三种方案,则正确的方案是( )甲:只需要满足BE=DF
乙:只需要满足AE=CF
丙:只需要满足AE∥CF
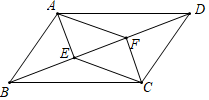 A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是10. 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( )
A、甲、乙、丙都是 B、只有甲、丙才是 C、只有甲、乙才是 D、只有乙、丙才是10. 若弹簧的总长度y(cm)是所挂重物x(千克)的一次函数,图象如图所示,由图可知,不挂重物时,弹簧的长度是( ) A、7cm B、8.5cm C、9cm D、10cm11. 如图所示,函数y=2x和y=ax+4的图象相交于点A( ,3),则关于x的不等式2x≥ax+4的解集为( )
A、7cm B、8.5cm C、9cm D、10cm11. 如图所示,函数y=2x和y=ax+4的图象相交于点A( ,3),则关于x的不等式2x≥ax+4的解集为( ) A、x≤ B、x≤3 C、x≥ D、x≥312. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( )
A、x≤ B、x≤3 C、x≥ D、x≥312. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得关于x,y的二元一次方程组的解是( )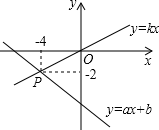 A、 B、 C、 D、13. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、 B、 C、 D、13. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )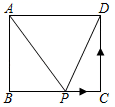 A、
A、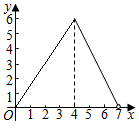 B、
B、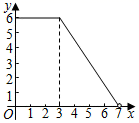 C、
C、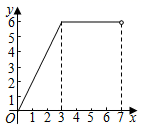 D、
D、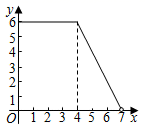 14. 如图,甲、丙两地相距500km,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系.根据图中提供的信息,下列说法错误的是( )
14. 如图,甲、丙两地相距500km,一列快车从甲地驶往丙地,途中经过乙地;一列慢车从乙地驶往丙地,两车同时出发,同向而行,折线ABCD表示两车之间的距离y(km)与慢车行驶的时间为x(h)之间的函数关系.根据图中提供的信息,下列说法错误的是( ) A、甲、乙两地之间的距离为200 km B、快车从甲地驶到丙地共用了2.5 h C、快车速度是慢车速度的1.5倍 D、快车到达丙地时,慢车距丙地还有50 km
A、甲、乙两地之间的距离为200 km B、快车从甲地驶到丙地共用了2.5 h C、快车速度是慢车速度的1.5倍 D、快车到达丙地时,慢车距丙地还有50 km二、填空题
-
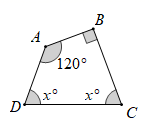
15. 点P(3,﹣5)关于x轴对称的点的坐标为 .16. 如图,则x的值为.
 17. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD= .18. 下表是某商店出售货物时其数量x(个)与售价y(元)的对应关系表:
17. 已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD= .18. 下表是某商店出售货物时其数量x(个)与售价y(元)的对应关系表:数量x(个)
1
2
3
4
5
售价y(元)
8+0.2
16+0.2
24+0.2
32+0.2
40+0.2
根据表中提供的信息可知y与x之间的关系式是 .
19. 如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为 . 20. 如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.
20. 如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.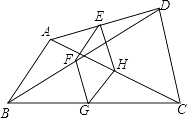
三、解答题
-
21. 已知一次函数的图象经过点 和 .(1)、求该函数图象与x轴的交点坐标;(2)、判断点 是否在该函数图象上.22. 小刚计算一个多边形的内角和求得结果为900°.老师指出他的计算结果不对.小刚重新检查,发现多数了一条边.(1)、你知道这个多边形是几边形吗?你是怎么知道的?(2)、这个多边形的内角和与外角和有什么样的数量关系?23. 已知点A(a,3),B(b,6),C(5,c),AC⊥x轴,BC⊥y轴,且点B在第二象限的角平分线上.
 (1)、求出A,B,C三点的坐标.(2)、求△ABC的面积.24. 某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题
(1)、求出A,B,C三点的坐标.(2)、求△ABC的面积.24. 某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题 (1)、求这次被调查的学生人数.(2)、请将条形统计图补充完整.(3)、求出扇形统计图中B对应的圆心角的度数.25. 如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE.
(1)、求这次被调查的学生人数.(2)、请将条形统计图补充完整.(3)、求出扇形统计图中B对应的圆心角的度数.25. 如图,已知四边形ABCD为平行四边形,AE,CF分别平分∠BAD和∠BCD,交BD于点E,F,连接AF,CE. (1)、若∠BCF=65°,求∠ABC的度数;(2)、求证:四边形AECF是平行四边形.26. 甲、乙两人相约春游去登山,山高300米,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、若∠BCF=65°,求∠ABC的度数;(2)、求证:四边形AECF是平行四边形.26. 甲、乙两人相约春游去登山,山高300米,甲、乙两人距地面的高度y(米)与登山时间x(分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: (1)、b=m;(2)、若乙提速后,乙登山的速度是甲登山速度3倍;
(1)、b=m;(2)、若乙提速后,乙登山的速度是甲登山速度3倍;①则t= ▲ min;
②登山多长时间乙追上了甲,求出此时x的值;
③在上山过程中,先到达山顶的一人原地休息等待另一人,当甲、乙两人距地面高度差为50m时,求出此时x的值.