河北省承德市兴隆县2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 在圆的面积公式S=πR2中,变量是( )A、S、π、R B、S、R C、π、R D、只有R2. 为了维护我国的海洋权益,我海军在海战演习中,欲确定每艘战舰的位置,需要知道每艘战舰相对我方潜艇的( )A、距离 B、方位角 C、距离和方位角 D、以上都不对3. 下列函数中是正比例函数的是( )A、 B、 C、 D、4. 如图是小明、小刚小红做课间操时的位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,那么小红的位置可表示为( )
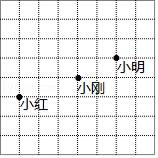 A、(1,3) B、(-2,3) C、(-1,3) D、(0,2)5. 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( )
A、(1,3) B、(-2,3) C、(-1,3) D、(0,2)5. 在一次科学探测活动中,探测人员发现一目标在如图所示的阴影区域内,则目标的坐标可能是( ) A、(-30,100) B、(70,-50) C、(90,60) D、(-20,-80)6. 函数y=的自变量的取值范围是( )A、x≥3 B、x>3 C、x≠0且x≠3 D、x≠07. 下列各图象中不表示y是x的函数的是( )A、
A、(-30,100) B、(70,-50) C、(90,60) D、(-20,-80)6. 函数y=的自变量的取值范围是( )A、x≥3 B、x>3 C、x≠0且x≠3 D、x≠07. 下列各图象中不表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知油箱中有油25升,每小时耗油5升,则剩油量P(升)与耗油时间t(小时)之间的函数关系式为( )A、P=25+5t B、P=25-5t C、P= D、P=5t-259. 已知点P位于第二象限,距y轴3个单位长度,距x轴4个单位长度,则点P的坐标是( )A、(-3,4) B、(3,-4) C、(4,-3) D、(-4,3)10. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、11. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:
8. 已知油箱中有油25升,每小时耗油5升,则剩油量P(升)与耗油时间t(小时)之间的函数关系式为( )A、P=25+5t B、P=25-5t C、P= D、P=5t-259. 已知点P位于第二象限,距y轴3个单位长度,距x轴4个单位长度,则点P的坐标是( )A、(-3,4) B、(3,-4) C、(4,-3) D、(-4,3)10. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、11. 弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的质量x(kg)间有下面的关系:X
0
1
2
3
4
5
Y
10
10.5
11
11.5
12
12.5
下列说法错误的是( )
A、x与y都是变量,且x是自变量; B、所挂物体质量为4kg时,弹簧长度为12cm; C、弹簧不挂重物时的长度为0cm; D、物体质量每增加1kg,弹簧长度y增加0.5cm.12.如图,在3×3的正方形网格中由四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( )
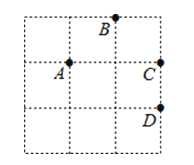 A、A点 B、B点 C、C点 D、D点13. 已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )
A、A点 B、B点 C、C点 D、D点13. 已知点P为某个封闭图形边界上的一定点,动点M从点P出发,沿其边界顺时针匀速运动一周,设点M的运动时间为x,线段PM的长度为y,表示y与x的函数图象大致如图所示,则该封闭图形可能是( )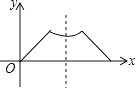 A、
A、 B、
B、 C、
C、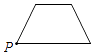 D、
D、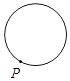 14. 关于一次函数y=x-1,下列说法:①图象与y轴的交点坐标是(0,-1);②y随x的增大而增大;③图象经过第一、二、三象限; ④直线y=x-1可以看作由直线y=x向右平移1个单位得到.其中正确的有( )A、1个 B、2个 C、3个 D、4个15. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是( )
14. 关于一次函数y=x-1,下列说法:①图象与y轴的交点坐标是(0,-1);②y随x的增大而增大;③图象经过第一、二、三象限; ④直线y=x-1可以看作由直线y=x向右平移1个单位得到.其中正确的有( )A、1个 B、2个 C、3个 D、4个15. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是( )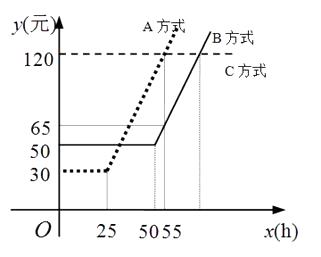 A、每月上网时间不足25 h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱16. 如图,在平面直角坐标系中,的顶点坐标分别为 , , . 当直线与有交点时,b的取值范围是( )
A、每月上网时间不足25 h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱16. 如图,在平面直角坐标系中,的顶点坐标分别为 , , . 当直线与有交点时,b的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 已知等腰三角形的周长为24,底边y关于腰长x的函数解析式是 .18. 阅读下面材料:小明想探究函数的性质,他借助计算器求出了y与x的几组对应值,并在平面直角坐标系中画出了函数图象:
x
…
-3
-2
-1
1
2
3
…
y
…
2.83
1.73
0
0
1.73
2.83
…

小聪看了一眼就说:“你画的图象肯定是错误的.”
请回答:
①小聪判断的理由是 .
②当时,x的值为 .
③请写出函数的一条性质: .
19. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位:km).笔直铁路经过A,B两地. (1)、A,B间的距离km;(2)、计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使 , 则AD的长为km.
(1)、A,B间的距离km;(2)、计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使 , 则AD的长为km.三、解答题
-
20. 已知一次函数的图象过点M(3,2 ),N(-1,-6 )两点,求一次函数的表达式.21. 已知:一次函数y=-x+2的图象分别与x轴、y轴交于点A、B.
 (1)、请直接写出A,B两点坐标:A、B(2)、在直角坐标系中画出函数图象;(3)、若平面内有一点C(5,3),请连接AC、BC,则△ABC是三角形.22. 三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
(1)、请直接写出A,B两点坐标:A、B(2)、在直角坐标系中画出函数图象;(3)、若平面内有一点C(5,3),请连接AC、BC,则△ABC是三角形.22. 三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.( 1 )建立适当的直角坐标系,并写出各个顶点的坐标;
( 2 )将(1)中各顶点的横坐标都加2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
( 3 )将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
( 4 )将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
23. 已知y是的正比例函数,当时, .(1)、求出y与x的函数关系式;(2)、当时,求y的值;(3)、当时,求x的值;24. 如图,直线的解析表达式为: , 且直线与x轴交于点D,直线经过点A(4,0), , 直线 , 交于点C. (1)、求点D的坐标;(2)、求直线的解析表达式;(3)、求△ADC的面积;(4)、在直线上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.25. 我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)、求点D的坐标;(2)、求直线的解析表达式;(3)、求△ADC的面积;(4)、在直线上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.25. 我市从 2018 年 1 月 1 日开始,禁止燃油助力车上路,于是电动自 行车的市场需求量日渐增多.某商店计划最多投入 8 万元购进 A、B 两种型号的 电动自行车共 30 辆,其中每辆 B 型电动自行车比每辆 A 型电动自行车多 500 元.用 5 万元购进的 A 型电动自行车与用 6 万元购进的 B 型电动自行车数量一 样.
(1)、求 A、B 两种型号电动自行车的进货单价;
(2)、若 A 型电动自行车每辆售价为 2800 元,B 型电动自行车每辆售价为 3500 元,设该商店计划购进 A 型电动自行车 m 辆,两种型号的电动自行车全部销售 后可获利润 y 元.写出 y 与 m 之间的函数关系式;
(3)、该商店如何进货才能获得最大利润?此时最大利润是多少元?
26. 如图,直线OC、BC的函数关系式分别为y=x和y=﹣2x+b,且交点C的横坐标为2,动点P(x,0)在线段OB上移动(0<x<3). (1)、求点C的坐标和b;(2)、若点A(0,1),当x为何值时,AP+CP的值最小;(3)、过点P作直线EF⊥x轴,分别交直线OC、BC于点E、F.
(1)、求点C的坐标和b;(2)、若点A(0,1),当x为何值时,AP+CP的值最小;(3)、过点P作直线EF⊥x轴,分别交直线OC、BC于点E、F.①若EF=3,求点P的坐标.
②设△OBC中位于直线EF左侧部分的面积为s,请写出s与x之间的函数关系式,并写出自变量的取值范围.