河北省沧州市泊头市2021-2022学年八年级下学期期末考试数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(1,-2022)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列函数中,自变量x的取值范围是 的函数是( )A、 B、 C、 D、3. 根据“五项管理”和“双减”政策要求,要充分保障学生睡眠的质量.沧州市某中学为了解本校1200名学生的睡眠情况,从中抽查了200名学生的睡眠时间进行统计,下面叙述正确的是( )A、以上调查属于全面调查 B、200名学生是样本容量 C、1200名学生是总体的一个样本 D、每名学生的睡眠时间是一个个体4. 下列结论中,矩形具有而平行四边形不一定具有的性质是( )A、对边平行且相等 B、对角线互相平分 C、任意两个邻角互补 D、对角线相等5. 如图,表示A点的位置,正确的是( )
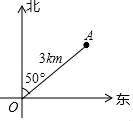 A、距O点3km的地方 B、在O点的东北方向上 C、在O点东偏北40°的方向 D、在O点北偏东50°方向,距O点3km的地方6. 一次函数图像如图所示,则k和b的取值范围是( )
A、距O点3km的地方 B、在O点的东北方向上 C、在O点东偏北40°的方向 D、在O点北偏东50°方向,距O点3km的地方6. 一次函数图像如图所示,则k和b的取值范围是( ) A、 , B、 , C、 , D、 ,7. 已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )A、0.4和0.3 B、0.4和9 C、12和0.3 D、12和98. 若n边形的内角和等于外角和的4倍,则边数n是( )A、8 B、9 C、10 D、119. 如图,三个顶点坐标是、、 , 那么顶点D的坐标是( )
A、 , B、 , C、 , D、 ,7. 已知样本数据个数为30,且被分成4组,各组数据个数之比为2:4:3:1,则第二小组和第三小组的频率分别为( )A、0.4和0.3 B、0.4和9 C、12和0.3 D、12和98. 若n边形的内角和等于外角和的4倍,则边数n是( )A、8 B、9 C、10 D、119. 如图,三个顶点坐标是、、 , 那么顶点D的坐标是( )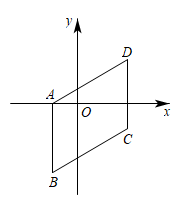 A、(2,1) B、(2,2) C、(3,1) D、(3,2)10. 新冠病毒抗原检测方便快捷,一般15-20分钟可出结果.在2022年4月太原新冠疫情防控中,小店区投入大量资金为居民发放抗原检测试剂盒进行抗原检测.小明用表格表示总价w与试剂盒数量n之间的关系,根据表格数据,下列说法错误的是( )
A、(2,1) B、(2,2) C、(3,1) D、(3,2)10. 新冠病毒抗原检测方便快捷,一般15-20分钟可出结果.在2022年4月太原新冠疫情防控中,小店区投入大量资金为居民发放抗原检测试剂盒进行抗原检测.小明用表格表示总价w与试剂盒数量n之间的关系,根据表格数据,下列说法错误的是( )试剂盒数量n(盒)
…
3
4
5
6
7
8
…
总价w(元)
…
45
60
75
90
105
120
…
A、在这个变化过程中,n是自变量,w是因变量 B、n每增加1盒,w增加15元 C、总价w与试剂盒数量n的关系式为w=15n D、按照表格表示的规律,试剂盒数量为100盒时,总价为1200元11. 在一次“寻宝”游戏中,寻宝人已经找到两个标志点和 , 并且知道藏宝地点的坐标是 , 则藏宝处应为图中的( )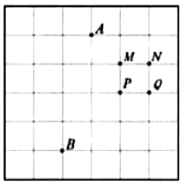 A、点M B、点N C、点P D、点Q12. 线段EF是由线段PQ平移得到的,点的对应点为 , 则点的对应点F的坐标为( )A、(-8,3) B、(-8,-5) C、(2,-5) D、(2,3)13. 已知点(-3,y1)、(4,y2)在函数 y=-2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定14. 如图,在的两边上分别截取OA、OB,使;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC,连接AB、OC交于点D.若 , 四边形OACB的面积为.点E为CB的中点,连接DE,则线段DE的长为( )
A、点M B、点N C、点P D、点Q12. 线段EF是由线段PQ平移得到的,点的对应点为 , 则点的对应点F的坐标为( )A、(-8,3) B、(-8,-5) C、(2,-5) D、(2,3)13. 已知点(-3,y1)、(4,y2)在函数 y=-2x+1 图像上,则y1与y2的大小关系是( )A、y1>y2 B、y1=y2 C、y1<y2 D、无法确定14. 如图,在的两边上分别截取OA、OB,使;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC,连接AB、OC交于点D.若 , 四边形OACB的面积为.点E为CB的中点,连接DE,则线段DE的长为( )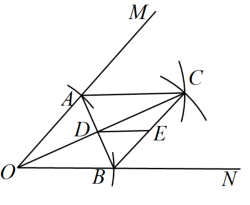 A、 B、 C、8 D、15. 某公司今年1~4月的电子产品销售总额如图1所示,其中平板电脑的销售额占当月电子产品销售总额的百分比如图2,据图中信息,得到的结论不合理的是( )
A、 B、 C、8 D、15. 某公司今年1~4月的电子产品销售总额如图1所示,其中平板电脑的销售额占当月电子产品销售总额的百分比如图2,据图中信息,得到的结论不合理的是( ) A、这4个月,电子产品销售总额为290万元 B、平板电脑销售额占当月电子产品销售总额的百分比,1月最高 C、这4个月,平板电脑销售额最低的是3月 D、平板电脑4月份的销售额比3月份有所下降16.
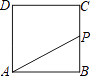
A、这4个月,电子产品销售总额为290万元 B、平板电脑销售额占当月电子产品销售总额的百分比,1月最高 C、这4个月,平板电脑销售额最低的是3月 D、平板电脑4月份的销售额比3月份有所下降16.如图,正方形ABCD的边长为4,现有一动点P从点A出发,沿A→B→C→D→A的路径以每秒1个单位长度的速度匀速运动,设点P运动的时间为t,△APB的面积为S,则下列图象能大致反映S与t的函数关系的是( )
 A、
A、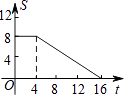 B、
B、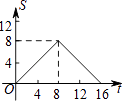 C、
C、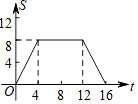 D、
D、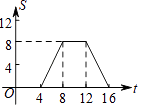
二、填空题
-
17. 若函数是一次函数,则m的值为.18. 牛奶中含有丰富的营养成分,其中水分约占82%;蛋白质约占4.3%,脂肪约占6%,乳糖约占7%,其它约占0.7%,对人体的健康有非常重要的作用.为直观地表示出各成分在总体中所占的百分比,最合适的统计图是.19. 已知关于x,y的方程组的解是 , 则在同一平面直角坐标系中存在两条直线:与 , 当时,则x的取值范围.20. 在平面直角坐标系中,对于平面内任意一点 , 若规定以下两种变换:
① . 如;
② , 如 .
按照以上变换有: , 那么 .
三、解答题
-
21. 在平面直角坐标系中,的位置如图所示.
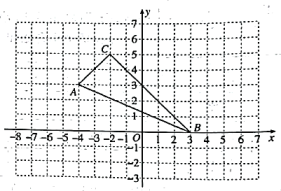 (1)、分别写出以下顶点的坐标:A;B;C;(2)、顶点A关于x轴的对称点坐标 , 顶点C关于原点的对称点坐标;(3)、作与关于y轴成轴对称的.22. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.
(1)、分别写出以下顶点的坐标:A;B;C;(2)、顶点A关于x轴的对称点坐标 , 顶点C关于原点的对称点坐标;(3)、作与关于y轴成轴对称的.22. 在①;②;③这三个条件中任选一个补充在下面横线上,并完成证明过程.已知,如图,四边形ABCD是平行四边形,对角线AC、BD相交于点O,点E、F在AC上,(填写序号).
23. 依据学习函数的经验,在平面直角坐标系中,作出函数的图像.(1)、列表:m=;n=;x
0
n
y=x+2
M
0
(2)、描点连线,画出函数的图象; (3)、若直线与直线交于点A,点B在直线上且横坐标为-4,连接OB,求的面积.24. “共同抗疫,爱卫同行”.某学校为了解学生关于新冠病毒防疫常识的掌握情况,特开展了网络防疫测试.某小组随机抽取部分学生的测试成绩x(满分100分),并进行整理分析,绘制了如下尚不完整的学生测试成绩频数分布表和频数分布直方图.根据以上信息,回答下列问题:
(3)、若直线与直线交于点A,点B在直线上且横坐标为-4,连接OB,求的面积.24. “共同抗疫,爱卫同行”.某学校为了解学生关于新冠病毒防疫常识的掌握情况,特开展了网络防疫测试.某小组随机抽取部分学生的测试成绩x(满分100分),并进行整理分析,绘制了如下尚不完整的学生测试成绩频数分布表和频数分布直方图.根据以上信息,回答下列问题:学生测试成绩频数分布表
组别
成绩x(分)
频数(人)
频率
A
4
0.1
B
10
0.25
C
m
n
D
8
0.2
E
6
0.15
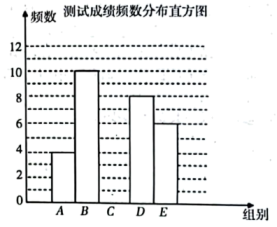 (1)、m= , n=;(2)、补全频数分布直方图;(3)、若要画出该组数据的扇形统计图,计算组别C对应的扇形圆心角的度数;(4)、若测试成绩不低于80分就可以获得“防疫小达人”奖章,若该校共有2000人参加此次知识测试,请估计获得“防疫小达人”奖章的人数.25. 随着冬奥会的举办,冬奥会的吉祥物“冰墩墩”越来越受到大家的喜爱,掀起了一阵抢购热潮.某商贩按进价48元/个,购进了一批吉祥物“冰墩墩”,在夜市上进行出售.为了方便,他带了一些零钱备用,在售出一部分后,又降价出售.售出的“冰墩墩”的个数x与他手中持有的钱数y(含备用零线)的关系如图所示,结合图像回答下列问题:
(1)、m= , n=;(2)、补全频数分布直方图;(3)、若要画出该组数据的扇形统计图,计算组别C对应的扇形圆心角的度数;(4)、若测试成绩不低于80分就可以获得“防疫小达人”奖章,若该校共有2000人参加此次知识测试,请估计获得“防疫小达人”奖章的人数.25. 随着冬奥会的举办,冬奥会的吉祥物“冰墩墩”越来越受到大家的喜爱,掀起了一阵抢购热潮.某商贩按进价48元/个,购进了一批吉祥物“冰墩墩”,在夜市上进行出售.为了方便,他带了一些零钱备用,在售出一部分后,又降价出售.售出的“冰墩墩”的个数x与他手中持有的钱数y(含备用零线)的关系如图所示,结合图像回答下列问题: (1)、当时,求y与x之间的关系式;(2)、冬奥会结束后,人们抢购热情也有所消减,商贩将每个“冰墩墩”降价12元后继续销售,这批冰墩墩完全出售后,这时他手中的钱(含备用的线)是8400元,问他一共购进了多少个“冰墩墩”?(3)、这个商贩一共赚了多少钱?26. 如图,点O为坐标原点,四边形OABC为矩形, , , 点D是OA的中点,动点P在线段CB上以每秒4个单位长度的速度由点C向点B运动.设动点P的运动时间为t秒.
(1)、当时,求y与x之间的关系式;(2)、冬奥会结束后,人们抢购热情也有所消减,商贩将每个“冰墩墩”降价12元后继续销售,这批冰墩墩完全出售后,这时他手中的钱(含备用的线)是8400元,问他一共购进了多少个“冰墩墩”?(3)、这个商贩一共赚了多少钱?26. 如图,点O为坐标原点,四边形OABC为矩形, , , 点D是OA的中点,动点P在线段CB上以每秒4个单位长度的速度由点C向点B运动.设动点P的运动时间为t秒.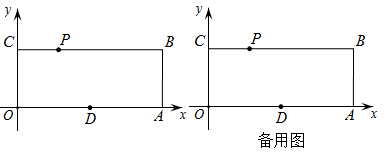 (1)、点P的坐标为(用含t的代数式表示);(2)、当四边形PODB是平行四边形时,求t的值;(3)、在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出点Q的坐标;若不存在,说明理由.
(1)、点P的坐标为(用含t的代数式表示);(2)、当四边形PODB是平行四边形时,求t的值;(3)、在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出点Q的坐标;若不存在,说明理由.