河北省保定市高阳县2021-2022学年八年级下学期期末考试数学试题

试卷更新日期：2023-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{9}$ C、 $\sqrt{8}$ D、 $\sqrt{3}$

查看试题解析
2. 已知正比例函数 $y = 3 x$ 的图象经过点 $(m ， 1)$ ，则m的值为（）

A、 $\frac{1}{3}$ B、3 C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
3. 在▱ABCD中，如果∠A+∠C＝140°，那么∠C等于（　　）．

A、70° B、60° C、40° D、20°

查看试题解析
4. 如图，在平面直角坐标系中，一次函数 $y = - 2 x + 1$ 的图像可以是（）

A、① B、② C、③ D、④

查看试题解析
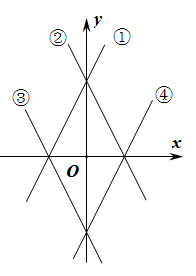5. “□”覆盖了等式“ $\sqrt{18}$ □ $\sqrt{2}$ ＝3”中的运算符号，则“□”覆盖的是（）

A、＋ B、 $-$ C、 $\times$ D、 $\div$

查看试题解析
6. 下列四组数据中，不能作为直角三角形三边长的是（）

A、5，12，13 B、2，3，4 C、1， $\sqrt{2}$ ， $\sqrt{3}$ D、1，2， $\sqrt{5}$

查看试题解析
7. 若二次根式 $\sqrt{1 - x}$ 与 $\sqrt{2}$ 能合并，则x的最大整数值是（）

A、﹣7 B、﹣1 C、0 D、2

查看试题解析
8. 某校八年级在建党100周年合唱比赛中，9位评委分别给出八年级一班的原始评分，评定该班成绩时，从9个原始评分中去掉一个最高分、一个最低分，得到7个有效评分，7个有效评分与9个原始评分相比，这两组数据一定不变的是（）．

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
9. 如图，在 $∠ M O N$ 的两边上分别截取 $O A 、 O B$ ，使 $O A = O B$ ；分别以点A、B为圆心， $O A$ 长为半径作弧，两弧交于点C；连接 $A C 、 B C 、 A B 、 O C$ ．若 $A B = 2 c m$ ，四边形 $O A C B$ 的面积为 $4 c m^{2}$ 则 $O C$ 的长为（）

A、2 B、3 C、4 D、5

查看试题解析
10. 《九章算术》是我国古代一部著名的数学专著，其中记载了一个“折竹抵地”问题：今有竹高一丈，末折抵地，去本三尺，问折者高几何？其意思是：有一根与地面垂直且高一丈的竹子（1丈＝10尺），现被大风折断成两截，尖端落在地面上，竹尖与竹根的距离为三尺．问折断处高地面的距离为（）

A、5.45尺 B、4.55尺 C、5.8尺 D、4.2尺

查看试题解析
11. 某校人工智能科普社团有12名成员，成员的年龄情况统计如下：
年龄（岁）
12
13
14
15
16
人数（人）
1
4
3
2
2
则这12名成员的平均年龄是（）

A、13岁 B、14岁 C、15岁 D、16岁

查看试题解析
12. 为了研究特殊四边形，李老师制作了这样一个教具（如图1）：用钉子将四根木条钉成一个平行四边形框架ABCD，并在A与C、B与D两点之间分别用一根橡皮筋拉直固定，课上，李老师右手拿住木条BC，用左手向右推动框架至AB⊥BC（如图2）观察所得到的四边形，下列判断正确的是（）

A、∠BCA＝45° B、AC＝BD C、BD的长度变小 D、AC⊥BD

查看试题解析
13. 如图，直线y＝﹣x＋a与y＝x＋b的交点的横坐标为﹣2，两直线与x轴交点的横坐标分别是﹣1，﹣3，则关于x的不等式﹣x＋a＞x＋b＞0的解集是（）

A、x＞﹣2 B、x＜﹣2 C、﹣3＜x＜﹣2 D、﹣3＜x＜﹣1

查看试题解析
14. 某轮滑队所有队员的年龄只有12、13、14、15、16（岁）五种情况，其中部分数据如图所示，若队员年龄的唯一的众数与中位数相等，则这个轮滑队队员人数m最小是（）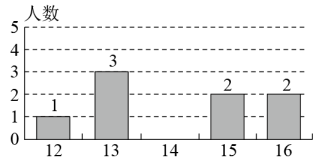

A、9 B、10 C、11 D、12

查看试题解析
15. 在将式子 $\frac{m}{\sqrt{m}}$ （m＞0）化简时，
小明的方法是： $\frac{m}{\sqrt{m}}$ = $\frac{m^{} \sqrt{m}}{\sqrt{m} \cdot \sqrt{m}}$ = $\frac{m \sqrt{m}}{m}$ = $\sqrt{m}$ ；

小亮的方法是： $\frac{m}{\sqrt{m}} = \frac{{(\sqrt{m})}^{2}}{\sqrt{m}} = \sqrt{m}$ ；

小丽的方法是： $\frac{m}{\sqrt{m}} = \frac{\sqrt{m^{2}}}{\sqrt{m}} = \sqrt{\frac{m^{2}}{m}} = \sqrt{m}$ .

则下列说法正确的是（　　）

A、小明、小亮的方法正确，小丽的方法错误 B、小明、小丽的方法正确，小亮的方法错误 C、小明、小亮、小丽的方法都正确 D、小明、小丽、小亮的方法都错误

查看试题解析
16. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A、1，4，5 B、2，3，5 C、3，4，5 D、2，2，4

查看试题解析

二、填空题

17. 计算： $\sqrt{48} - \sqrt{12} = a \sqrt{3} - 2 \sqrt{b} = c \sqrt{3}$ ，则a=；b+c= ．

查看试题解析
18. 根据如图的程序计算，当输入 $x = 3$ 时，输出的结果y=；当输出的结果 $y = 5.7$ 时，则输入x= ．

查看试题解析
19. 如图1，在平面直角坐标系xOy中，▱ABCD的面积为10，且边AB在x轴上．如果将直线y＝﹣x沿x轴正方向平移，在平移过程中，记该直线在x轴上平移的距离为m，直线被平行四边形的边所截得的线段的长度为n，且n与m的对应关系如图2所示，那么图2中a的值是， b的值是．

查看试题解析

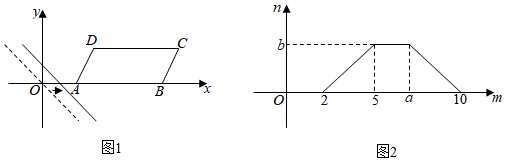
三、解答题

20. 已知： $A = (\sqrt{2} +) (\sqrt{2} - 1)$ ， “□”表示一个数．

(1)、若 $= 1$ ，求A的值；

(2)、若 $= - 1$ ，求A的值．

查看试题解析
21. 如图，在 $△ A B C$ 中，点D、E分别为 $A B$ 、 $B C$ 的中点，点F在 $A C$ 的延长线上， $D E = C F$ ．求证： $D C ∥ E F$ ．

查看试题解析
22. 如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画出图形．

(1)、在图1中，画一个正方形，使它的面积是10；

(2)、在图2中，画一个三角形，使它的三边长分别为3， $\sqrt{10}$ ， $\sqrt{13}$ ；

(3)、在图3中，画一个三角形，使它的三边长都是无理数，并且构成的三角形是直角三角形．

查看试题解析
23. 6月的第三个星期天是父亲节，某校组织了以“父爱如山”为主题的演讲比赛，根据初赛成绩，七、八年级各选出5名学生组成代表队，参加决赛．并根据他们的决赛成绩绘制了如下两幅统计图表：（满分为100分）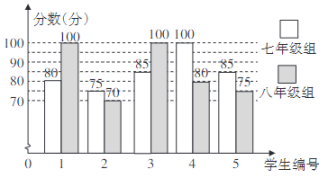

(1)、补全下表中的数据；
组别
平均数
中位数
众数
方差
七年级
85
八年级
85
100
160

(2)、结合两队决赛成绩的平均数和中位数，评价两个队的决赛成绩；

(3)、哪个年级代表队的决赛成绩更稳定．

查看试题解析
24. 某零售店销售甲、乙两种蔬菜，甲种蔬菜每千克获利1.1元，乙种蔬菜每千克获利1.5元．该店计划一次购进这两种蔬菜共56千克，并能全部售出．设该店购进甲种蔬菜x千克，销售这56千克蔬菜获得的总利润为y元．

(1)、求y与x的关系式；

(2)、若乙种蔬菜的进货量不超过甲种蔬菜的 $\frac{5}{2}$ ，则该店购进甲、乙两种蔬菜各多少千克时，获得的总利润最大？

(3)、由于蔬菜自身的特点，有 $\frac{1}{3}$ 的乙种蔬菜需要保鲜处理，每千克的保鲜费用是a元（ $a > 0$ ）．若获得的总利润随x的增大而减小，请直接写出a的取值范围．

查看试题解析
25. 如图，在菱形 $A B C D$ 中， $A B = 2$ ， $∠ D A B = 60 °$ ，点E是 $A D$ 边的中点．点M是 $A B$ 边上一动点（不与点A重合），连接 $M E$ 并延长交 $C D$ 的延长线于点N，连接 $M D$ 、 $A N$ ．

(1)、求证：四边形 $A M D N$ 是平行四边形；

(2)、当 $A M = 1$ 时，求证：四边形 $A M D N$ 是矩形；

(3)、填空：当 $A M$ 的值为时，四边形 $A M D N$ 是菱形．

查看试题解析
26. 如图，在平面直角坐标系中，直线AB分别交x轴，y轴于点A（3，0），点B（0，3）．

(1)、求直线AB的解析式；

(2)、若点C是线段AB上的一个动点，当△AOC的面积为3时，求出此时点C的坐标；

(3)、在（2）的条件下，在x轴上是否存在一点P，使得△COP是等腰三角形？若存在，直接写出所有满足条件的点P的坐标，若不存在，请说明理由．

查看试题解析

组别	平均数	中位数	众数	方差
七年级		85
八年级	85		100	160

年龄（岁）	12	13	14	15	16
人数（人）	1	4	3	2	2