北京市燕山地区2021-2022学年八年级下学期期末质量监测数学试题

试卷更新日期：2023-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各组数中，不能作为直角三角形三边长的是（）

A、6，8，10 B、7，24，25 C、8，15，17 D、13，14，15

查看试题解析
2. 将直线y＝2x向下平移3个单位长度后，得到的直线是（）

A、y＝2x＋3 B、y＝2x－3 C、y＝2(x＋3) D、y＝2(x－3)

查看试题解析
3. 一次函数y＝-3x-4的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图，▱ABCD中，∠B＋∠D＝100°，则∠A＝（）

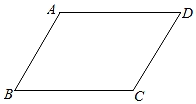A、50° B、80° C、100° D、130°

查看试题解析
5. 下列计算正确的是（）

A、 $\sqrt{9}$ ＝±3 B、 $\sqrt{2}$ ＋ $\sqrt{5}$ ＝ $\sqrt{7}$ C、 $\sqrt{(- 2)^{2}}$ ＝2 D、 $\sqrt{6}$ ÷ $\sqrt{2}$ ＝3

查看试题解析
6. 一次数学课后，李老师布置了6道选择题作为课后作业，课代表小丽统计了本班35名同学的答题情况，结果如右图所示，则在全班同学答对的题目数这组数据中，众数和中位数分别是（）

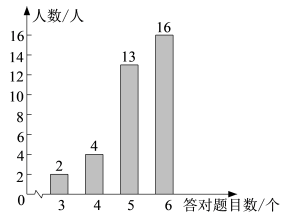A、5，6 B、6，5 C、6，5.5 D、6，6

查看试题解析
7. 图1是第七届国际数学教育大会(ICME－7)的会徽图案，它是由一串有公共顶点O的直角三角形（如图2所示）演化而成的．如果图2中的OA₁＝A₁A₂＝A₂A₃＝…＝A₇A₈＝1，那么OA₈的长为（）

A、 $\sqrt{5}$ B、 $\sqrt{6}$ C、 $2 \sqrt{2}$ D、3

查看试题解析
8. 如图，有一个装水的容器，容器内的水面高度是10cm，水面面积是100cm² ．现向容器内注水，并同时开始计时．在注水过程中，水面高度以每秒0.2cm的速度匀速增加．容器注满水之前，容器内水面的高度h，注水量V随对应的注水时间t的变化而变化，则h与t，V与t满足的函数关系分别是（）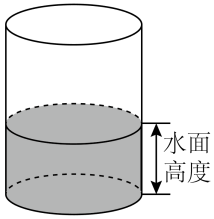

A、正比例函数关系，正比例函数关系 B、正比例函数关系，一次函数关系 C、一次函数关系，一次函数关系 D、一次函数关系，正比例函数关系

查看试题解析

二、填空题

9. 点P(1，6)在正比例函数 $y = k x (k \neq 0)$ 的图像上，则k的值为．

查看试题解析
10. 若式子 $\sqrt{x - 3}$ 有意义，则实数 $x$ 的取值范围是.

查看试题解析
11. 如图，▱ABCD中，对角线AC，BD相交于点O，再添加一个条件，使得四边形ABCD是矩形，可添加的条件是． (写出一个条件即可)

查看试题解析
12. 如图，菱形ABCD的对角线AC，BD相交于点O，E为DC的中点，若 $O E = 2$ ，则菱形的周长为．

查看试题解析
13. 如图，一次函数y＝x＋2与 $y = k x + b (k \neq 0)$ 的图像交于点P，则关于x，y的二元一次方程组 ${\begin{array}{l} y = x + 2 \\ y = k x + b \end{array}$ 的解是．

查看试题解析
14. 一次函数 $y = k x + b (k \neq 0)$ 的图像上有两个点P₁(－2， $y_{1}$ )，P₂(1， $y_{2}$ )，且 $y_{1}$ ＞ $y_{2}$ ，请写出一个满足条件的函数解析式：．

查看试题解析
15. 某学校拟招聘一名数学教师，一位应聘者在说课和答辩两个环节的成绩分别是85和90，学校给出这两个环节的平均成绩为86.5，可知此次招聘中，权重较大的是．（填“说课”或“答辩”）

查看试题解析
16. 随着北京冬奥会的成功举办，越来越多的人喜欢上冰雪运动．为了解当地一家滑雪场的经营情况，小聪对该滑雪场自2022年1月31日至2月13日共两周的日接待游客数（单位：千人）进行了统计，并绘制成下面的统计图．
根据统计图提供的信息，有下列三个结论：
①按日接待游客数从高到低排名，2月6日在这14天中排名第4；
②记第一周，第二周日接待游客数的方差分别为s₁² ， s₂² ，则s₁²＞s₂²；
③这14天日接待游客数的众数和中位数都是2.0千人．
其中所有正确结论的序号是．

查看试题解析

三、解答题

17. 计算： $| - \sqrt{3} | + \sqrt{12} - 3 \sqrt{\frac{1}{3}}$ ．

查看试题解析
18. 如图，在 $▱$ ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．

查看试题解析
19. 下面是小芸设计的“作平行四边形ABCD的边AB的中点”的尺规作图过程．
已知：▱ABCD．
求作：点P，使点P为边AB的中点．
作法：
①作射线DA；
②以点A为圆心，BC长为半径画弧，
在点A左侧与射线DA交于点E；
③连接CE交AB于点P．
点P即为所求作的边AB的中点．
根据小芸设计的尺规作图过程，

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接AC，EB，
∵四边形ABCD是平行四边形，
∴AE∥BC．
∵AE＝      ▲       ，
∴四边形EBCA是平行四边形，（                            ）（填推理的依据）
∴AP＝PB，（                            ）（填推理的依据）
点P即为所求作的边AB的中点．

查看试题解析
20. 已知 $a = \sqrt{5} - 1$ ，求代数式 $a^{2} + 2 a - 5$ 的值．

查看试题解析
21. 已知一次函数 $y = k x + b (k \neq 0)$ 的图像经过点A(0，－2)，B(3，4)．

(1)、求出此一次函数的解析式；

(2)、求出该一次函数与x轴交点的坐标．

查看试题解析
22. 绿都农场有一块菜地如图所示，现测得AB＝12m，BC＝13m，CD＝4m，AD＝3m，∠D＝90°，求这块菜地的面积．

查看试题解析
23. 如图，矩形ABCD中，点O是对角线AC的中点，过点O作EF⊥AC分别交BC，AD于点E，F，连接AE和CF．

(1)、求证：四边形AECF为菱形；

(2)、若AB＝3，BC＝5，求AE的长．

查看试题解析
24. 某班“数学兴趣小组”根据学习一次函数的经验，对函数y＝｜x－2｜的图像和性质进行了研究．探究过程如下，请补充完整．

(1)、自变量x的取值范围是全体实数．下表是y与x的几组对应值：
x
…
－3
－2
－1
0
1
2
3
4
5
…
y
…
5
4
m
2
1
0
1
2
3
…
其中，m＝；

(2)、如下图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，并画出了函数图象的一部分，请画出该函数图象的另一部分；

(3)、观察函数图象发现，该函数图象的最低点坐标是；
当x＜2时，y随x的增大而减小；当x≥2时，y随x的增大而；

(4)、进一步探究，
①不等式｜x－2｜≥1.5的解集是；
②若关于x的方程｜x－2｜＝kx (k≠0)只有一个解，则k的取值范围是．

查看试题解析
25. 某中学为了解家长对课后延时服务的满意度，从七，八年级中各随机抽取50名学生家长进行问卷调查，获得了每位学生家长对课后延时服务的评分数据(记为x)，并对数据进行整理、描述和分析．下面给出了部分信息：
a．八年级课后延时服务家长评分数据的频数分布表如下（数据分为5组：0≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：
分组
频数
0≤x＜60
2
60≤x＜70
5
70≤x＜80
15
80≤x＜90
a
90≤x≤100
8
合计
50
b．八年级课后延时服务家长评分在80≤x＜90这一组的数据按从小到大的顺序排列，前5个数据如下：
81，81，82，83，83．
c．七，八年级课后延时服务家长评分的平均数，中位数，众数如下表：
年级
平均数
中位数
众数
七
78
79
85
八
81
b
83
根据以上信息，回答下列问题：

(1)、表中a＝， b＝．

(2)、你认为年级的课后延时服务开展得较好，理由是．（至少从两个不同的角度说明理由）

(3)、已知该校八年级共有600名学生家长参加了此次调查评分，请你估计其中大约有多少名家长的评分不低于80分．

查看试题解析
26. 如图，过正方形ABCD的顶点D作直线l交CB的延长线于点E，交AB边于点F，过点B作BG⊥DE，垂足为点G，连接AG．

(1)、依题意补全图形；

(2)、求证：∠ABG＝∠ADF；

(3)、用等式表示线段AG，BG，DG之间的数量关系，并证明．

查看试题解析
27. 对于平面直角坐标系xOy中的点M(m，0)和点P，给出如下定义：
若在y轴上存在点N，使得∠MNP＝90°，且NM＝NP，则称点P为m直角等腰点．例如，点P(－2，0)为2直角等腰点，理由如下：如图，设M(2，0)，以MP为斜边作等腰直角△PMN，可得y轴上的一个点N(0，2)，所以点P(－2，0)为2直角等腰点．

(1)、在点A(－1，0)，B(0，1)，C(1，1)中，是1直角等腰点的是；

(2)、若点D是直线y＝2x＋3上一点，且点D是3直角等腰点，求点D的坐标；

(3)、若一次函数y＝kx＋b(k≠0)的图像上存在无数个4直角等腰点，请直接写出该一次函数的解析式．

查看试题解析

分组	频数
0≤x＜60	2
60≤x＜70	5
70≤x＜80	15
80≤x＜90	a
90≤x≤100	8
合计	50

x	…	－3	－2	－1	0	1	2	3	4	5	…
y	…	5	4	m	2	1	0	1	2	3	…

年级	平均数	中位数	众数
七	78	79	85
八	81	b	83