山西省忻州市宁武县2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 点 $M (2 ， 4)$ 向下平移2个单位长度，得到的点的坐标是（）

A、 $(2 ， 2)$ B、 $(0 ， 2)$ C、 $(4 ， 4)$ D、 $(2 ， 6)$

查看试题解析
2. 在频数分布直方图中，用来表示各组频数的是每个矩形的（）

A、长 B、宽（高） C、周长 D、面积

查看试题解析
3. 下列不等式中，一元一次不等式有（）
① $x^{2} + 3 > 2 x$ ② $\frac{1}{x} - 3 > 0$ ③ $x - 3 > 2 y$
④ $\frac{x - 1}{π} \geq 5 π$ ⑤ $3 y > - 3$

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
4. 如图，数轴上点M所表示的数为m，则m的值是（）

A、 $\sqrt{5}$ －2 B、 $\sqrt{5}$ －1 C、 $\sqrt{5}$ ＋1 D、1－ $\sqrt{5}$

查看试题解析
5. 如图，平行线 $A B$ ， $C D$ 被直线 $A E$ 所截， $∠ 1 = 110 °$ ，则下列结论正确的是（）

A、 $∠ 2 = 110 °$ B、 $∠ 3 = 70 °$ C、 $∠ 4 = 70 °$ D、 $∠ 5 = 70 °$

查看试题解析
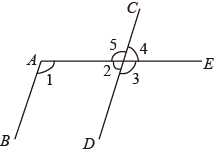6. 已知a，b满足（a+1）²-（b-2） $\sqrt{2 - b}$ +|c-3|＝0，则a+b+c的值等于（）

A、2 B、3 C、4 D、5

查看试题解析
7. 不等式组 ${\begin{array}{l} 2 x - 1 \geq 4 x + 5 \\ x > m \end{array}$ 有两个整数解，则m的取值范围为（　　）

A、﹣5＜m≤﹣4 B、﹣5＜m＜﹣4 C、﹣5≤m＜﹣4 D、﹣5≤m≤﹣4

查看试题解析
8. 已知A点的坐标为（3，a＋3），B点的坐标为（a，4），AB∥x轴，则线段AB的长为（）

A、5 B、4 C、3 D、2

查看试题解析
9. 七（1）班班长买钢笔和铅笔共30支，其中钢笔的支数比铅笔支数的2倍少3支.若设买钢笔 $x$ 支，铅笔 $y$ 支，根据题意，可得方程组（）

A、 ${\begin{array}{l} x + y = 30 \\ y = 2 x + 3 \end{array}$ B、 ${\begin{array}{l} x + y = 30 \\ y = 2 x - 3 \end{array}$ C、 ${\begin{array}{l} x + y = 30 \\ x = 2 y + 3 \end{array}$ D、 ${\begin{array}{l} x + y = 30 \\ x = 2 y - 3 \end{array}$

查看试题解析
10. 如图所示，直线 $A B$ ， $C D$ 相交于点 $O$ ， “阿基米德曲线”从点 $O$ 开始生成，如果将该曲线与每条射线的交点依次标记为1， $- 2$ ， 3， $- 4$ ， 5， $- 6$ …．那么标记为“ $- 2022$ ”的点在（）

A、射线 $O A$ 上 B、射线 $O B$ 上 C、射线 $O C$ 上 D、射线 $O D$ 上

查看试题解析

二、填空题

11. 调查神舟九号宇宙飞船各部件功能是否符合要求，这种调查适合用（填“普查”或“抽样调查”）．

查看试题解析
12. 已知 $(m - 4) x^{| m - 3 |} + 2 > 6$ 是关于x的一元一次不等式，则m的值为．

查看试题解析
13. 若关于x，y的方程组 ${\begin{array}{l} x + 2 y = 3 k - 1 \\ 2 x + y = 7 \end{array}$ 解满足 $0 < x + y < 5$ ，则k的取值范围是．

查看试题解析
14. 如图，下列条件中：① $∠ B + ∠ B C D = 180 °$ ；② $∠ 1 = ∠ 2$ ；③ $∠ 3 = ∠ 4$ ；④ $∠ B = ∠ 5$ ；则一定能判定AB//CD的条件有（填写所有正确的序号）．

查看试题解析
15. 已知P点坐标为（4-a，3a+9），且点P在 $x$ 轴上，则点P的坐标是．

查看试题解析

三、解答题

16.

(1)、计算： $\sqrt{4} + \sqrt[3]{27} + | \sqrt{3} - 3 | - \sqrt{{(- 3)}^{2}}$ ；

(2)、解方程组 ${\begin{array}{l} 3 x - 4 (x - 2 y) = 5 \\ x - 2 y = 1 \end{array}$ ；

(3)、解不等式组 ${\begin{array}{l} 3 x < 5 x + 6 \\ \frac{x + 1}{6} \geq \frac{x - 1}{2} \end{array}$ ，并把它的解集在数轴（如图）上表示出来．

查看试题解析
17. 当k为何值时，方程组 ${\begin{array}{l} 3 m - 2 n = 2 k \\ 2 m + 7 n = k - 18 \end{array}$ 的解m，n的值互为相反数？

查看试题解析
18. 阅读材料：我们已经学过利用“代入消元法”和“加减消元法”来解二元一次方程组，通过查阅相关资料，“勤奋组”的同学们发现在解方程组： ${\begin{array}{l} 2 x + y = 0 ① \\ 4 x + 3 y = 6 ② \end{array}$ 时可以采用一种“整体代入”的解法．
解：将方程②变形为4x＋2y＋y＝6，即2（2x＋y）＋y＝6③，把方程①代入方程③，得2×0＋y＝6．
所以y＝6，把y＝6代入方程①得x＝-3，所以方程组的解为 ${\begin{array}{l} x = - 3 \\ y = 6 \end{array}$ ．请你利用“整体代入”法解方程组： ${\begin{array}{l} 2 x - y = 5 \\ 5 x - 3 y = 20 \end{array}$ ．

查看试题解析
19. 如图，已知 $∠ 1 = ∠ 2$ ， $∠ 5 = ∠ 6$ ， $∠ 3 = ∠ 4$ ，试说明 $A E ∥ B D$ ， $A D ∥ B C$ ．请完成下列证明过程．
证明：∵ $∠ 5 = ∠ 6$ ，
∴ $A B ∥$   ▲  （       ），
∴ $∠ 3 =$   ▲  （    ）．
∵ $∠ 3 = ∠ 4$ ，
∴ $∠ 4 = ∠ B D C$ （      ）；
∴  ▲  // $B D$ （      ），
∴∠2=∠ADB，
∵∠1=∠2，
∴ $∠ 1 =$   ▲    ，
∴ $A D ∥ B C$ （       ）．

查看试题解析
20. 某社区从5000户家庭中随机抽取100户，调查他们家庭每月的平均用水量，并将调查的结果绘制成两幅不完整的统计图表：
平均用水a（吨）
3＜a≤6
6＜a≤9
9＜a≤12
12＜a≤15
15＜a≤18
频数
10
m
36
25
9
频率
0.1
0.2
0.36
n
0.09
请根据上面的统计图表，解答下列问题：

(1)、在频数分布表中：m＝， n＝．

(2)、根据题中数据补全频数分布直方图；

(3)、如果自来水公司将基本月用水量定为每户每月12吨，不超过基本月用水量的部分享受基本价格，超出基本月用水量的部分实行加价收费，那么该社区用户中约有多少户家庭能够全部享受基本价格？

查看试题解析
21. 2022年北京冬奥会、冬残奥会已圆满结束，活泼敦厚的“冰墩墩”，喜庆祥和的“雪容融”引起广大民众的喜爱．王老师想要购买这两种吉祥物作为本次冬奥会的纪念品，已知购买2件“冰墩墩”和1件“雪容融”共需150元，购买3件“冰墩墩”和2件“雪容融”共需245元．

(1)、求“冰墩墩”和“雪容融”的单价；

(2)、学校现需一次性购买上述型号的“冰墩墩”和“雪容融”纪念品共100个，要求购买的总费用不超过5000元，则最多可以购买多少个“冰墩墩”？

查看试题解析
22. 感知：解不等式 $\frac{x + 2}{x - 1} > 0$ ．根据两数相除，同号得正，异号得负，得不等式组 $① {\begin{array}{l} x + 2 > 0 ， \\ x - 1 > 0 \end{array}$ 或不等式组 $② {\begin{array}{l} x + 2 < 0 ， \\ x - 1 < 0 . \end{array}$ 解不等式组 $①$ ，得 $x > 1$ ；解不等式组 $②$ ，得 $x < - 2$ ，所以原不等式的解集为 $x > 1$ 或 $x < - 2$ ．

(1)、探究：解不等式 $\frac{2 x - 4}{x + 1} < 0$ ．

(2)、应用：不等式 $(x - 3) (x + 5) \leq 0$ 的解集是．

查看试题解析
23. 如图，在平面直角坐标系中，已知△ABC中，点A坐标为（4，0），点B的坐标是（2，3），点C在x轴的负半轴上，且AC=6．

(1)、写出点C的坐标（，）

(2)、在y轴上是否存在点P，使得S_△POB＝ $\frac{2}{3}$ S_△ABC，若存在，求出点P的坐标；若不存在；

(3)、把点C往上平移3个单位得到点H，画射线CH，连接BH，点M在射线CH上运动（不与点C、H重合）．试探索∠BMA、∠HBM、∠MAC之间的数量关系，并证明你的结论．

查看试题解析

平均用水a（吨）	3＜a≤6	6＜a≤9	9＜a≤12	12＜a≤15	15＜a≤18
频数	10	m	36	25	9
频率	0.1	0.2	0.36	n	0.09