山西省吕梁市交口县2020-2021学年七年级下学期期末数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 下列是无理数的是( )A、 B、1.414 C、 D、0.92. 2022年,在中国举办了第二十四届冬季奥林匹克运动会,图中是吉祥物“冰墩墩”,将图中的“冰墩墩”通过平移可以得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 已知 ,则下列不等式成立的是A、 B、 C、 D、4. 在平面直角坐标系中,点( , )所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列调查中,最适合采用全面调查(普查)方式的是( )A、调查我国最大的航天器“天和”核心舱零件的质量情况 B、调查全国中小学生收看央视一套播出的大型公益节目《开学第一课》的收视率 C、调查某一批LED灯的使用寿命 D、调查我省居民进行垃圾分类的情况6. 若关于 , 的二元一次方程的一组解为 , 则的值为( )A、 B、 C、1 D、27. 如图,已知∠1+∠2=180°,∠3=55°,那么∠4的度数是( )
3. 已知 ,则下列不等式成立的是A、 B、 C、 D、4. 在平面直角坐标系中,点( , )所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列调查中,最适合采用全面调查(普查)方式的是( )A、调查我国最大的航天器“天和”核心舱零件的质量情况 B、调查全国中小学生收看央视一套播出的大型公益节目《开学第一课》的收视率 C、调查某一批LED灯的使用寿命 D、调查我省居民进行垃圾分类的情况6. 若关于 , 的二元一次方程的一组解为 , 则的值为( )A、 B、 C、1 D、27. 如图,已知∠1+∠2=180°,∠3=55°,那么∠4的度数是( ) A、35° B、45° C、55° D、125°8. 用“加减法”将方程组中的x消去后得到的方程是( )A、 B、 C、 D、9. 不等式组的解集在数轴上表示为( )A、
A、35° B、45° C、55° D、125°8. 用“加减法”将方程组中的x消去后得到的方程是( )A、 B、 C、 D、9. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 10. 《九章算术》是我国东汉初年编订的一部数学经典著作,在它的“方程”里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排的,如图1、图2图中各行从左到右列出的算筹分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 类似地,图2所示的算筹图我们可以表述为( )
10. 《九章算术》是我国东汉初年编订的一部数学经典著作,在它的“方程”里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排的,如图1、图2图中各行从左到右列出的算筹分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 类似地,图2所示的算筹图我们可以表述为( )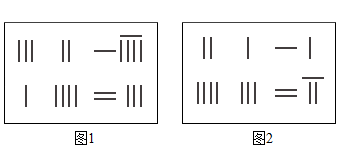 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 写出一个解是 的二元一次方程组:.12. 已知点P(2-a,3a)在第二象限,那么a的取值范围是 .13. 下列三个日常现象:

其中,可以用“垂线段最短”来解释的是 (填序号).
14. 为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,得到分数段在70.5~80.5的频数是50,所占百分比25%,则本次抽样调查的样本容量为.15. 在平面直角坐标系中,点 经过某种变换后得到点 ,我们把点 叫做点 的终结点.已知点 的终结点为 ,点 的终结点为 ,点 的终结点为 ,这样依次得到 、 、 、 、… ,若点 的坐标为 ,则点 的坐标为 .三、解答题
-
16.(1)、计算:(2)、解方程组:17. 解不等式组: ,并把解集在数轴上表示出来.18. 如图所示,三角形三个顶点 , , 的坐标分别为 , , .
 (1)、三角形向左平移2个单位长度,再向上平移3个单位长度,恰好得到三角形 , 试写出三角形三个顶点的坐标;(2)、求三角形的面积.19. 推理填空:如图, , , , 试说明 .
(1)、三角形向左平移2个单位长度,再向上平移3个单位长度,恰好得到三角形 , 试写出三角形三个顶点的坐标;(2)、求三角形的面积.19. 推理填空:如图, , , , 试说明 .
理由:∵(已知),
∴ ▲ ( )∴ ▲ ,
∵(已知),∴ ▲ , 又∵(已知),
∴ ▲ + ▲ ( ),即 ▲ ,
∴( ).
20. 以“创新”为发展理念的中国科技取得了举世瞩目的成就,某校就下列科技:A(中国“天眼”开启地外文明搜索)、B(天问一号的升空)、C(嫦娥五号探月)、D(北斗三号全球卫星导航)最感兴趣的成就随机抽取本校部分学生进行问卷调查(每人必选且只选一项),如图是整理数据后绘制的两幅不完整的统计图.
请你根据图中提供的信息回答下列问题:
(1)、本次接受问卷调查的有 ▲ 人,并补全条形统计图;(2)、选项B所对应扇形圆心角为;(3)、估计该校2200名学生中,对选项C感兴趣的有多少名学生?21. 阅读与探究本学期我们在第六章《实数》中,学习了平方根和立方根,下表是平方根和立方根的部分内容.
平方根
立方根
定义
一般地,如果一个数的平方等于 , 那么这个数叫做的平方根或二次方根.这就是说,如果 , 那么叫做的平方根.
一般地,如果一个数的立方等于 , 那么这个数叫做的立方根或三次方根.这就是说,如果 , 那么叫做的立方根.
运算
求一个数的平方根的运算,叫做开平方.开平方与平方互为逆运算.
求一个数的立方根的运算,叫做开立方.开立方与立方互为逆运算.
特征
正数有两个平方根,他们互为相反数;0的平方根是0;负数没有平方根.
正数的立方根是正数,0的立方根是0;负数的立方根是负数.
表示方法
正数的平方根可以用“”表示,读作“正负根号”.
一个数的立方根可以用“” 表示,读作“三次根号”.
今天我们类比平方根和立方根的学习方法学习四次方根.
(1)、探究定义:填写下表.1
16
类比平方根和立方根的定义,给四次方根下定义: .
(2)、探究性质:①81的四次方根是 ▲ ;0的四次方根是 ▲ ; ▲ (填“有”或“没有”)四次方根.②类比平方根和立方根的性质,归纳四次方根的性质: ▲ .
(3)、在探索过程中,你用到了哪些数学思想?请写出两个: .(4)、拓展应用①(将结果直接填到横线上)
②比较大小:(填“>”、“=”或“<”)
22. 习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”,某校为提高学生的阅读品味,现决定购买《艾青诗选》和《格列佛游记》两种书,已知购买2本《艾青诗选》和1本《格列佛游记》需100元;购买6本《艾青诗选》与购买7本《格列佛游记》的价格相同.(1)、求这两种书的单价各多少元?(2)、若要购买《艾青诗选》和《格列佛游记》共50本,且购买两种书的总价不超过1600元,请问至多要购买《艾青诗选》多少本?23. 综合与实践:折纸中的数学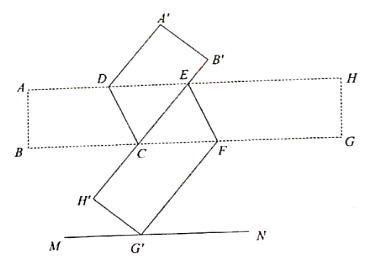
知识背景
我们在七年级上册第四章《几何图形初步》中探究了简单图形折叠问题,并进行了简单的计算与推理.七年级下册第五章我们学习了平行线的性质与判定,今天我们继续探究:折纸中的数学——长方形纸条的折叠与平行线.
(1)、知识初探
如图1,长方形纸条 中, , , .将长方形纸条沿直线 折叠,点 落在 处,点 落在 处, 交 于点 .若 ,求 的度数.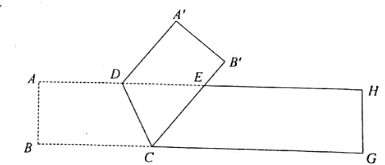 (2)、类比再探
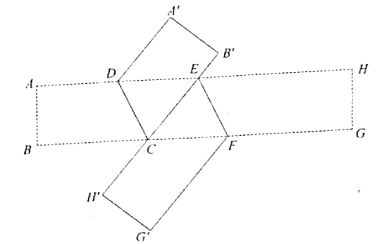
(2)、类比再探如图2,在图1的基础上将 对折,点 落在直线 上的 处.点 落在 处,得到折痕 ,则折痕 与 有怎样的位置关系?说明理由.
 (3)、拓展延伸
(3)、拓展延伸如图3,在图2的基础上,过点 作 的平行线 ,请你猜想 和 的数量关系,并说明理由.
