内蒙古自治区通辽市科尔沁左翼中旗2021-2022学年七年级下学期期末数学试题

试卷更新日期：2023-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数 $\frac{11}{3}$ ， 0， $\sqrt[3]{- 1}$ ， 3.1415926， $\sqrt{7}$ ， $\sqrt{16}$ ， $4 . \dot{2} \dot{1}$ ， $π$ ， 1.353353335…中，无理数的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若 $m > n$ ，下列不等式一定成立的是 $($ 　　 $)$

A、 $m - 2 > n + 2$ B、 $2 m > 2 n$ C、 $- \frac{m}{2} > \frac{n}{2}$ D、 $m^{2} > n^{2}$

查看试题解析
3. 如图，30°的直角三角板的顶点A、B分别在直线a，b上．若a∥b，∠1=45°，则∠2的度数为（）

A、10° B、15° C、20° D、25°

查看试题解析
4. 下列问题中，应采用全面调查的是（）

A、检测某品牌儿童鲜奶是否符合食品卫生标准 B、调查人民对冰墩墩的喜爱情况 C、调查与一新冠肺炎感染者密切接触人群 D、了解全国中学生的视力和用眼卫生情况

查看试题解析
5. 《九章算术》是中国古代第一部数学专著，书中有这样一题：“今有共买物，人出八，盈三；人出七，不足四．问人数、物价各几何？”大意是：有几个人一起去买一件物品，每人出8元，多3元；每人出7元，少4元，问有多少人？该物品价格是多少？设共有 $x$ 个人，该物品价格是 $y$ 元，则下列方程组正确的是（）

A、 ${\begin{array}{l} 8 x + 3 = y \\ 7 x - 4 = y \end{array}$ B、 ${\begin{array}{l} 8 y + 3 = x \\ 7 y - 4 = x \end{array}$ C、 ${\begin{array}{l} 8 x - 3 = y \\ 7 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 8 y - 3 = x \\ 7 y + 4 = x \end{array}$

查看试题解析
6. $\sqrt{81}$ 的平方根是（）

A、±3 B、3 C、±9 D、9

查看试题解析
7. 如图所示，在灌溉农田时，要把河（直线 $l$ 表示一条河）中的水引到农田 $P$ 处，设计了四条路线 $P A 、 P B 、 P C 、 P D$ ，你选择哪条路线挖渠才能使渠道最短（）

A、 $P A$ B、 $P B$ C、 $P C$ D、 $P D$

查看试题解析
8. 在平面直角坐标系中，点（﹣1，m²+1）一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 若关于x，y的方程组 ${\begin{array}{l} x + 2 y = m \\ x - y = 4 m \end{array}$ 的解是二元一次方程 $3 x + 2 y = 14$ 的一个解，则m的值是（）

A、1 B、-1 C、2 D、-2

查看试题解析
10. 若关于 $x$ 的不等式组 ${\begin{array}{l} x > a - 1 \\ 3 x \leq 2 (x + 2) \end{array}$ 至多有4个整数解，则 $a$ 的取值范围是（）

A、 $a > 1$ B、 $a \geq 1$ C、 $a > 2$ D、 $a \geq 2$

查看试题解析

二、填空题

11. 平面直角坐标系数中某点M（a，a＋1）在x轴上，则a＝

查看试题解析
12. 当 $x$ 时，式子 $3 x - 5$ 的值不大于 $5 x + 3$ 的值．

查看试题解析
13. 如图，已知AB∥DE，∠ABC＝75°，∠CDE＝150°，则∠BCD的度数为．

查看试题解析
14. 若不等式组 ${\begin{array}{l} x - a > 2 \\ b - 3 x > 0 \end{array}$ 解集是-1<x<1，则 ${(a + b)}^{2018}$ = ．

查看试题解析
15. 一个数的平方根是a+4和2a+5，则a= ，这个正数是．

查看试题解析
16. 某校为了解学生喜爱的体育活动项目，随机抽查了100名学生，让每人选一项自己喜欢的项目，并制成如图所示的扇形统计图如果该校有810名学生，则喜爱跳绳的学生约有人.

查看试题解析
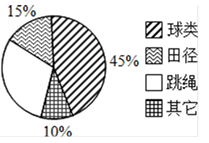17. 如图，在平面直角坐标系中，点A₁(1，2)，A₂(2，0)，A₃(3，－2)，A₄(4，0)……根据这个规律，探究可得点A₂₀₁₇的坐标是.

查看试题解析

三、解答题

18. 解方程组 ${\begin{array}{l} 2 x + y = 4 ① \\ x + 2 y = 2 ② \end{array}$ ．

查看试题解析
19. 解不等式组 ${\begin{array}{l} \frac{1}{2} (x + 1) \leq 2 \\ \frac{x + 2}{2} > \frac{x + 3}{3} \end{array}$ 并求出不等式组的整数解之和．

查看试题解析
20. 看图填空：
已知：如图， $E$ 为 $D F$ 上的点， $B$ 为 $A C$ 上的点， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D ．$ 求证： $A C / / D F$ ．

证明：

$∵ ∠ 1 = ∠ 2 ($    $)$

$∠ 1 = ∠ 3$ ， $∠ 2 = ∠ 4 ($     $)$

$∴ ∠ 3 = ∠ 4 ($      $)$

$∴$   ▲   $/ /$   ▲

$∴ ∠ C = ∠ A B D ($     ）

又 $∵ ∠ C = ∠ D ($      $)$

$∴ ∠ D = ∠ A B D ($     ）

$∴ A C / / D F ($      $)$

查看试题解析
21. △ABC与△A₁B₁C₁在平面直角坐标系中的位置如图所示．

(1)、分别写出下列各点的坐标：A、B、C；

(2)、△ABC是由△A₁B₁C₁经过怎样的平移得到的?

(3)、若点P（x，y）是△ABC内部一点，求△A₁B₁C₁内部的对应点P₁的坐标；

(4)、求△ABC的面积．

查看试题解析
22. 八年级（1）班研究性学习小组为研究全校同学课外阅读情况，在全校随机邀请了部分同学参与问卷调查，统计同学们一个月阅读课外书的数量，并绘制了以下统计图.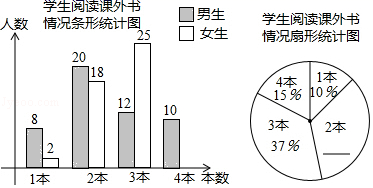

请根据图中信息解决下列问题：

(1)、共有多少名同学参与问卷调查；

(2)、补全条形统计图和扇形统计图；

(3)、全校共有学生1500人，请估计该校学生一个月阅读2本课外书的人数约为多少.

查看试题解析
23. 观察下列各式，并用所得出的规律解决问题：

(1)、 $\sqrt{2} \approx 1.414$ ， $\sqrt{200} \approx 14.14$ ， $\sqrt{20000} \approx 141.4$ ， ……
$\sqrt{0.03} \approx 0.1732$ ， $\sqrt{3} \approx 1.732$ ， $\sqrt{300} \approx 17.32$ ， ……
由此可见，被开方数的小数点每向右移动位，其算术平方根的小数点向移动位．

(2)、已知 $\sqrt{15} \approx 3.873$ ， $\sqrt{1.5} \approx 1.225$ ，则 $\sqrt{150} \approx$ ； $\sqrt{0.15} \approx$ ．

(3)、 $\sqrt[3]{1} = 1$ ， $\sqrt[3]{1000} = 10$ ， $\sqrt[3]{1000000} = 100$ ， ……
小数点的变化规律是．

(4)、已知 $\sqrt[3]{10} \approx 2.154$ ， $\sqrt[3]{y} \approx - 0.2154$ ，则 $y =$ ．

查看试题解析
24. 为了响应市委和市政府“绿色环保，节能减排”的号召，幸福商场用3300元购进甲、乙两种节能灯共计100只，很快售完．这两种节能灯的进价、售价如下表：

进价（元/只）
售价(元/只）
甲种节能灯
30
40
乙种节能灯
35
50

(1)、求幸福商场甲、乙两种节能灯各购进了多少只?

(2)、全部售完100只节能灯后，商场共计获利多少元？

查看试题解析
25. 为了抓住世博会商机，某商店决定购进A、B两种世博会纪念品，若购进A种纪念品10件，B种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．

(1)、求购进A、B两种纪念品每件各需多少元？

(2)、若该商店决定拿出4000元全部用来购进这两种纪念品，考虑市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且不超过B钟纪念品数量的8倍，那么该商店共有几种进货方案？

(3)、若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？最大利润是多少？

查看试题解析

	进价（元/只）	售价(元/只）
甲种节能灯	30	40
乙种节能灯	35	50