河北省秦皇岛市卢龙县2021-2022学年七年级下学期期末考试数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 以下列长度为边不能构成三角形的是( )A、1、2、3 B、2、2、3 C、2、3、3 D、2、3、42. 下列命题是真命题的是( )A、如果 , 那么a=b B、如果两个角是同位角,那么这两个角相等 C、相等的两个角是对顶角 D、平行于同一条直线的两条直线平行3. 的运算结果是( )A、 B、 C、 D、4. 把 写成 ( , 为整数)的形式,则 为( )A、 B、 C、 D、5. 如图,能判定EB∥AC的条件是( )
 A、∠C=∠ABE B、∠A=∠EBD C、∠C=∠DBE D、∠A=∠ABC6. 一副三角板如图摆放(直角顶点C互相重合),边AB、CD交于F点;DE∥BC.则∠AFC的度数是( )
A、∠C=∠ABE B、∠A=∠EBD C、∠C=∠DBE D、∠A=∠ABC6. 一副三角板如图摆放(直角顶点C互相重合),边AB、CD交于F点;DE∥BC.则∠AFC的度数是( ) A、60° B、75° C、100° D、105°7. 下列多项式:① ;② ;③ ;④ ,其中能用平方差公式分解因式的多项式有( )A、1个 B、2个 C、3个 D、4个8. 不等式 的解集在数轴上表示正确的是( )A、
A、60° B、75° C、100° D、105°7. 下列多项式:① ;② ;③ ;④ ,其中能用平方差公式分解因式的多项式有( )A、1个 B、2个 C、3个 D、4个8. 不等式 的解集在数轴上表示正确的是( )A、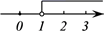 B、
B、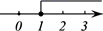 C、
C、 D、
D、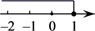 9. 下列条件能说明△ABC是直角三角形的是( )A、∠A=∠B=2∠C B、∠A=∠B+∠C C、∠A:∠B:∠C=2:3:4 D、∠A=40°,∠B=55°10. 已知a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( )
9. 下列条件能说明△ABC是直角三角形的是( )A、∠A=∠B=2∠C B、∠A=∠B+∠C C、∠A:∠B:∠C=2:3:4 D、∠A=40°,∠B=55°10. 已知a,b两个实数在数轴上的对应点如图所示,则下列各式一定成立的是( ) A、a-1>b-1 B、3a>3b C、-a>-b D、a+b>a-b11. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 812. 甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追赶乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )A、 B、 C、 D、13. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形14. 如图,△ABC的面积是1,AD是△ABC的中线,AF= FD,CE= EF,则△DEF的面积为( )
A、a-1>b-1 B、3a>3b C、-a>-b D、a+b>a-b11. 如果多项式 是一个完全平方式,则m的值是 ( )A、±4 B、4 C、8 D、± 812. 甲乙两人在相距18千米的两地,若同时出发相向而行,经2小时相遇;若同向而行,且甲比乙先出发1小时追赶乙,那么在乙出发后经4小时两人相遇,求甲、乙两人的速度.设甲的速度为x千米/小时,乙的速度为y千米/小时,则可列方程组为( )A、 B、 C、 D、13. 已知a、b、c是 的三条边,且满足 ,则 是( )A、锐角三角形 B、钝角三角形 C、等腰三角形 D、等边三角形14. 如图,△ABC的面积是1,AD是△ABC的中线,AF= FD,CE= EF,则△DEF的面积为( )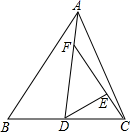 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 多项式 的公因式是 .16. 已知三角形的两边分别为和 , 则第三边的取值范围是 .17. 一元一次不等式的负整数解是.18. 如图,已知AD是△ABC的边BC上的中线,若AB=6,△ABD的周长比△ACD的周长多2,则AC= .
 19. 已知三角形的一个内角是另一个内角的两倍,当时,这个三角形的最小内角是.20. 已知等腰三角形的周长为15.其一边长为7,另外两边长分别是 .
19. 已知三角形的一个内角是另一个内角的两倍,当时,这个三角形的最小内角是.20. 已知等腰三角形的周长为15.其一边长为7,另外两边长分别是 .三、解答题
-
21.(1)、因式分解:3-6a +3.(2)、解不等式组: , 并把它的解集在数轴上表示出来.
 22. 已知是方程2x-ay=9的一个解,解决下列问题:(1)、求的值;(2)、化简并求值:23. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF.
22. 已知是方程2x-ay=9的一个解,解决下列问题:(1)、求的值;(2)、化简并求值:23. 如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E,点F为AC延长线上的一点,连接DF. (1)、求∠CBE的度数;(2)、若∠F=25°,求证:.24. 如图,是一道例题及部分解答过程,其中A、B是两个关于x,y的二项式.
(1)、求∠CBE的度数;(2)、若∠F=25°,求证:.24. 如图,是一道例题及部分解答过程,其中A、B是两个关于x,y的二项式.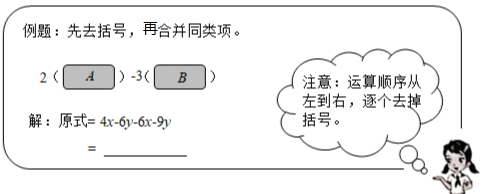
请仔细观察上面的例题及解答过程,完成下列问题∶
(1)、直接写出多项式A和 B,并求出该例题的运算结果;(2)、求多项式A与B的平方差.25. 某校学生社会实践小组开展调查,获取了本校食堂学生早餐的营养情况,如下是调查报告中的一部分,根据所得信息,解答下列问题.调查报告
1、早餐总质量为500g;
2、早餐的成分是蛋白质、脂肪、矿物质和碳水化合物;
3、所含蛋白质的质量与矿物质之比为4:1;
4、脂肪占早餐总质量的10%.
(1)、早餐中所含脂肪的质量是g.(2)、若早餐中蛋白质和碳水化合物所占百分比的和不高于85%,求早餐中所含碳水化合物质量的最大值.26. 有甲、乙两个长方形纸片,边长如图所示(m>0),面积分别为S甲和S乙 .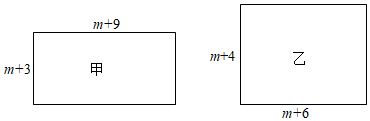 (1)、①计算:S甲= , S乙=;
(1)、①计算:S甲= , S乙=;②用“<”,“=”或“>”填空:S甲S乙 .
(2)、若一个正方形纸片的周长与乙长方形的周长相等,面积为S正 .①该正方形的边长是 ▲ 用含m的代数式表示);
②小方同学发现:S正与S乙的差与m无关.请判断小方的发现是否符合题意,并通过计算说明你的理由.