河北省保定市唐县2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 下面四个图形中,∠1=∠2一定成立的是( )A、
 B、
B、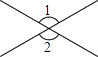 C、
C、 D、
D、 2. 北京成功举办了2022年冬奥会,吉祥物冰墩墩深受人们的喜爱,下面四个图案可以看作由“如图的冰墩墩”经过平移得到的是( )
2. 北京成功举办了2022年冬奥会,吉祥物冰墩墩深受人们的喜爱,下面四个图案可以看作由“如图的冰墩墩”经过平移得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列各式中,正确的是( )A、=±4 B、±=4 C、 D、=-44. 如图,在道路附近有一疫情重灾区,现需要紧挨道路选一点建临时防控指挥部,且使此重灾区到临时防控指挥部的距离最短,则此点是( )
3. 下列各式中,正确的是( )A、=±4 B、±=4 C、 D、=-44. 如图,在道路附近有一疫情重灾区,现需要紧挨道路选一点建临时防控指挥部,且使此重灾区到临时防控指挥部的距离最短,则此点是( ) A、A点 B、B点 C、C点 D、D点5. 下列调查中,适宜采用全面调查(普查)方式的是( )A、在新冠疫情高风险区的防范措施的调查 B、对我县初中生防溺水意识情况的调查 C、对保定市市民实施低碳生活情况的调查 D、对某个工厂口罩质量的调查6. 如图,将一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=23°,那么∠2的度数为( )
A、A点 B、B点 C、C点 D、D点5. 下列调查中,适宜采用全面调查(普查)方式的是( )A、在新冠疫情高风险区的防范措施的调查 B、对我县初中生防溺水意识情况的调查 C、对保定市市民实施低碳生活情况的调查 D、对某个工厂口罩质量的调查6. 如图,将一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=23°,那么∠2的度数为( ) A、22° B、23° C、25° D、30°7. 已知是方程的解,则的值为( )A、2 B、4 C、6 D、108. 如图,把两个边长为1的小正方形分别沿对角线剪开,将四个直角三角形拼成一个大的正方形,则这个大正方形的边长为( )
A、22° B、23° C、25° D、30°7. 已知是方程的解,则的值为( )A、2 B、4 C、6 D、108. 如图,把两个边长为1的小正方形分别沿对角线剪开,将四个直角三角形拼成一个大的正方形,则这个大正方形的边长为( ) A、2 B、1.5 C、 D、9. 已知a、b为两个连续的整数,a<<b且,则a+b=( )A、6 B、7 C、8 D、910. 医护人员身穿防护服,化身暖心“大白”到某校进行核酸检测.若每名“大白”检测200人,则有一名“大白”少检测18人;若每名“大白”检测180人,则余下42人.设该校共有师生x人,有y名“大白”来学校检测,根据题意,可列方程组为( )A、 B、 C、 D、11. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( )
A、2 B、1.5 C、 D、9. 已知a、b为两个连续的整数,a<<b且,则a+b=( )A、6 B、7 C、8 D、910. 医护人员身穿防护服,化身暖心“大白”到某校进行核酸检测.若每名“大白”检测200人,则有一名“大白”少检测18人;若每名“大白”检测180人,则余下42人.设该校共有师生x人,有y名“大白”来学校检测,根据题意,可列方程组为( )A、 B、 C、 D、11. 如图所示,给出下列条件:①∠1=∠B;②∠EFD+∠B=180°;③∠B=∠D;④∠E=∠B;⑤∠BFD=∠B.其中,一定能判断AB∥CD的条件的个数为( ) A、2个 B、3个 C、4个 D、5个12. 解方程组 时,由②-①得( )A、 B、 C、 D、13. 点P(a+6 ,a-2)在y轴上,则a的值为( )A、6 B、-6 C、2 D、-214. 在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿E折叠,若∠B′FB=70°,则∠AEF=( )
A、2个 B、3个 C、4个 D、5个12. 解方程组 时,由②-①得( )A、 B、 C、 D、13. 点P(a+6 ,a-2)在y轴上,则a的值为( )A、6 B、-6 C、2 D、-214. 在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD,点E在AD上,点F在BC上,把长方形纸带沿E折叠,若∠B′FB=70°,则∠AEF=( ) A、35° B、40° C、45° D、60°15. 如图,船C在观测站A的北偏东35°方向上,在观测站B的北偏西20°方向上,那么( )度.
A、35° B、40° C、45° D、60°15. 如图,船C在观测站A的北偏东35°方向上,在观测站B的北偏西20°方向上,那么( )度. A、20° B、35° C、55° D、60°16. 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2022个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A、20° B、35° C、55° D、60°16. 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2022个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( ) A、(-1,1) B、(-1,-1) C、(-1,-2) D、(0,-2)
A、(-1,1) B、(-1,-1) C、(-1,-2) D、(0,-2)二、填空题
-
17. 比较大小:(1)、1.414(2)、设a>b,则2a-52b-518. 在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(3,2)、(4,0),
 (1)、如图,若把△OAB沿x轴向右平移到△CDE,点D的坐标为把(6,2),则点E的坐标为 .(2)、若把△OAB沿x轴平移2个单位得到△CDE,则点D的坐标为 .19. 在平面直角坐标系中,已知点P(m-3,4-2m),m是任意实数.(1)、当m=0时,点P在第象限.(2)、当点P在第三象限时,求m的取值范围 .
(1)、如图,若把△OAB沿x轴向右平移到△CDE,点D的坐标为把(6,2),则点E的坐标为 .(2)、若把△OAB沿x轴平移2个单位得到△CDE,则点D的坐标为 .19. 在平面直角坐标系中,已知点P(m-3,4-2m),m是任意实数.(1)、当m=0时,点P在第象限.(2)、当点P在第三象限时,求m的取值范围 .三、解答题
-
20.(1)、(2)、21. 规定min(m,n)表示m,n中较小的数(m,n均为实数),例如:min{3,-1}=-1,min=据此解决下列问题:(1)、min{-2,- 3}= ;(2)、若min{3x-1,2}=2,求x的取值范围;22. 如图,直线AB∥CD,∠GEB的平分线EF交CD与点F,∠HGF=40°,求∠EFD的度数.
 23. 受疫情影响,国家推出了“网络授课”,使得初中学生越来越离不开手机,“沉迷手机”现象再次受到社会的关注,记者小吴随机调查了某小区若干名学生和家长对中学生配带手机的看法,统计整理并作了如图统计图:
23. 受疫情影响,国家推出了“网络授课”,使得初中学生越来越离不开手机,“沉迷手机”现象再次受到社会的关注,记者小吴随机调查了某小区若干名学生和家长对中学生配带手机的看法,统计整理并作了如图统计图:
根据统计图中提供的信息,解答下列问题:
(1)、求本次调查的家长总人数 .(2)、补全条形统计图,并求出家长“反对”带手机所占扇形圆心角的度数;(3)、估计该小区800名学生中“反对”配带手机的学生人数.24. 发现:如图,∠AOB内有一点P:过点P画PCOB交OA于点C,画PDOA交OB于点D;根据所画图形试说明:∠O与∠CPD的数量关系; (1)、验证:完善下面的解答过程,并填写理由或数学式:
(1)、验证:完善下面的解答过程,并填写理由或数学式:∵PCOB
∴∠O= ( )
∵ PDOA
∴∠CPD=
∴∠O=∠CPD
(2)、探究:某数学兴趣小组通过以上练习发现了命题“两边分别平行的两个角相等”,甲同学认为该命题是真命题并画了图1进行验证,乙同学对甲同学的判断提出质疑,认为该命题不一定成立,是假命题,并作图如图2所示,题设与甲同学相同,得到∠B≠∠D,根据乙同学的作图,试判断此时∠B与∠D的数量关系,并说明理由..

 (3)、归纳:综合甲乙两同学的证明得到结论:两边分别平行的两个角25. 新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.某超市计划购买A、B两种型号的口罩共96箱,通过市场调研发现,购买2箱A型口罩和3箱B型口罩共需340元,购买5箱A型口罩和2箱B型口罩需410元.(1)、购买A、B两种型号口罩每箱的价格分别是多少元?(2)、根据超市实际情况,购买这两种型号口罩的总费用不能超过5720元,该超市最多可以购买B种型号口罩多少箱?26. 如图,在以点O为原点的平面直角坐标系中点A , B的坐标分别为(a , 0),(a , b),点C在y轴上,且BC x轴,a , b满足 .点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到O为止).
(3)、归纳:综合甲乙两同学的证明得到结论:两边分别平行的两个角25. 新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.某超市计划购买A、B两种型号的口罩共96箱,通过市场调研发现,购买2箱A型口罩和3箱B型口罩共需340元,购买5箱A型口罩和2箱B型口罩需410元.(1)、购买A、B两种型号口罩每箱的价格分别是多少元?(2)、根据超市实际情况,购买这两种型号口罩的总费用不能超过5720元,该超市最多可以购买B种型号口罩多少箱?26. 如图,在以点O为原点的平面直角坐标系中点A , B的坐标分别为(a , 0),(a , b),点C在y轴上,且BC x轴,a , b满足 .点P从原点出发,以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线运动(回到O为止).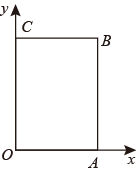 (1)、直接写出点A , B , C的坐标;(2)、当点P运动3秒时,连接PC , PO , 求出点P的坐标,并直接写出∠CPO , ∠BCP , ∠AOP之间满足的数量关系;(3)、点P运动t秒后(t≠0),是否存在点P到x轴的距离为 t个单位长度的情况.若存在,求出点P的坐标;若不存在,请说明理由.
(1)、直接写出点A , B , C的坐标;(2)、当点P运动3秒时,连接PC , PO , 求出点P的坐标,并直接写出∠CPO , ∠BCP , ∠AOP之间满足的数量关系;(3)、点P运动t秒后(t≠0),是否存在点P到x轴的距离为 t个单位长度的情况.若存在,求出点P的坐标;若不存在,请说明理由.