河北省保定市高阳县2021-2022学年七年级下学期期末考试数学试题

试卷更新日期：2023-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 平面直角坐标系内，点A（-2，-3）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在实数 $- \sqrt{5}$ ， $0 . \overset{·}{4} 2 \overset{·}{1}$ ， 3.14，0， $\frac{π}{2}$ ， $\frac{22}{7}$ ， $\sqrt{81}$ ， 0.1616616661……（两个1之间依次多一个6）中，无理数的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
3. 下列各组数值是二元一次方程 $2 x - y = 5$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 0 \\ y = 5 \end{array}$ C、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ D、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$

查看试题解析
4. 不等式 $- x - 2 \leq 0$ 的解集在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
5. 要了解某校 $1000$ 名初中生的课外负担情况，若采用抽样调查的方法进行调查，则下列样本选择最具有代表性的是（）

A、调查全体女生 B、调查全体男生 C、调查九年级全体学生 D、调查七、八、九年级各 $100$ 名学生

查看试题解析
6. 将点 $A (5 ， - 2)$ 按如下方式进行平移：先向上平移2个单位，再向左平移4个单位，则点A平移后的坐标为（）

A、（7，-6） B、（9，0） C、（1，-4） D、（1，0）

查看试题解析
7. 如图，在一张半透明的纸上画一条直线 $l$ ，在直线 $l$ 外任取一点 $A$ ，折出过点 $A$ 且与直线 $l$ 垂直的直线，这样的直线只能折出一条，理由是（）

A、连接直线外一点与直线上各点的所有线段中，垂线段最短 B、两点之间线段最短 C、在平面内，过一点有且只有一条直线与已知直线垂直 D、经过直线外一点有且只有一条直线与已知直线平行

查看试题解析
8. 空气是多种气体的混合物．空气主要由氮气、氧气、稀有气体（氦、氖、氩、氪、氙、氡、气奥），二氧化碳以及其他物质（如水蒸气、杂质等）组合而成．为直观介绍空气各成分的百分比，最适合用的统计图是（）

A、折线图 B、条形图 C、直方图 D、扇形图

查看试题解析
9. 如图，是一个由4条线段构成的“鱼”形图案，其中OA∥BC，AC∥OB.若∠1＝50°，则∠3的度数为（）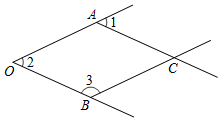

A、130° B、120° C、50° D、125°

查看试题解析
10. 如图所示，从A到B有 $① ② ③$ 三条路可以走，每条路长分别为L，M，N，则L，M，N的大小关系是 $()$ ．

A、 $L > M > N$ B、 $L = M > N$ C、 $M > N > L$ D、 $L > N > M$

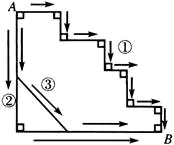查看试题解析
11. 下列命题是真命题的是（）

A、任何实数都有算术平方根 B、在平面直角坐标系中，点 $(3 ， 5)$ 与点 $(5 ， 3)$ 代表的位置相同 C、 $x = - 2$ 是不等式 $2 - 3 x > 0$ 的一个解 D、垂直于同一直线的两条直线互相平行

查看试题解析
12. 老师：若实数 $a$ ， $b$ ， $c$ 在数轴上对应点的位置如图所示，学生1： $a c > b c$ ；学生2： $a + b > c + b$ ；学生3： $a + c > b + c$ ；学生4： $a b > c b$ ．老师：只有1名学生的结论是正确的．这名学生是（）

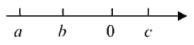A、学生1 B、学生2 C、学生3 D、学生4

查看试题解析
13. 如图，用边长为3的两个小正方形拼成一个大正方形，则大正方形的边长最接近的整数是（）

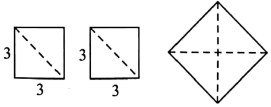A、3 B、4 C、5 D、6

查看试题解析
14. 把一些书分给几名同学，若每人分11本，则有剩余，若（），依题意，设有x名同学，可列不等式7（x+4）＞11x．

A、每人分7本，则剩余4本 B、每人分7本，则剩余的书可多分给4个人 C、每人分4本，则剩余7本 D、其中一个人分7本，则其他同学每人可分4本

查看试题解析
15. 明代数学家程大位的著作《算法统宗》中有一个“绳索量竿”问题：“一只竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托，问索长几尺？”译文为：“现有一根竹竿和一条绳索，用绳索去量竹竿，绳索比竹竿长5尺，如果将绳索对折后再去量竹竿，就比竹竿短5尺，问绳索长几尺？”（注：一托=5尺）设绳索长x尺，竹竿长y尺，根据题意列方程组正确的是（）

A、 ${\begin{array}{l} x - y = 5 \\ y - \frac{1}{2} x = 5 \end{array}$ B、 ${\begin{array}{l} x - y = 5 \\ y - 2 x = 5 \end{array}$ C、 ${\begin{array}{l} y - x = 5 \\ x - \frac{1}{2} y = 5 \end{array}$ D、 ${\begin{array}{l} y - x = 5 \\ y - 2 x = 5 \end{array}$

查看试题解析
16. 在平面直角坐标系 $x O y$ 中，对于任意一点 $P (x ， y)$ ，规定： $f (x ， y) = {\begin{array}{l} | x | ， | x | \geq | y | \\ | y | ， | x | < | y | \end{array}$ ；比如 $f (- 4 ， \frac{3}{2}) = 4 ， f (- 2 ， - 3) = 3$ ．当 $f (x ， y) = 2$ 时，所有满足该条件的点P组成的图形为（）

A、 B、 C、 D、

查看试题解析

二、填空题

17. 已知A（a，0），B（-3，0）且AB=5，则a= ．

查看试题解析
18. 依据图中呈现的运算关系，
可知： $a$ =； $b$ = ．

查看试题解析
19. 已知关于 $x$ ， $y$ 的二元一次方程 $k x - y = k - 1$ ．

(1)、当 $k = 1$ 和 $k = 2$ 时，所得两个方程组成的方程组是 ${\begin{array}{l} x - y = 0 \\ 2 x - y = 1 \end{array}$ ，这个方程组的解是；

(2)、当 $k = - 1$ 和 $k = - 2$ 时，所得两个方程组成的方程组是 ${\begin{array}{l} - x - y = - 2 \\ - 2 x - y = - 3 \end{array}$ ，这个方程组的解是；

(3)、猜想：无论 $k$ 取何值时，关于 $x$ ， $y$ 的方程 $k x - y = 2 k - 3$ 一定有一个解是．

查看试题解析

三、解答题

20. 计算

(1)、 $\sqrt{100 - 36} + \sqrt{(- \frac{1}{4})^{2}} - (\sqrt{5})^{2}$

(2)、已知 $8 x^{3} + 27 = 0$ ，求 $x$ 的值．

查看试题解析
21. 如图，平面内有两条直线l₁ ， l₂点A在直线l₁上，按要求画图并填空：

(1)、过点A画l₂的垂线段AB，垂足为点B；

(2)、过点A画直线AC⊥l₁ ，交直线l₂于点C；

(3)、过点A画直线AD∥l₂；

(4)、若AB＝12，AC＝13，则点A到直线l₂的距离等于．

查看试题解析
22. 如图，在平面直角坐标系 $x o y$ 中，A（4，0），C（0，6），点B在第一象限内，点P从原点O出发，以每秒2个单位长度的速度沿着长方形 $O A B C$ 的边逆时针移动一周（即：沿着O→A→B→C→O的路线移动）．

(1)、点B的坐标为；

(2)、当点P移动4s时，求出点P的坐标；

(3)、在移动过程中，当点P到 $x$ 轴的距离为5个单位长度时，求点P移动的时间t ．

查看试题解析
23. 阅读材料：
形如 $2 < 2 x + 1 < 3$ 的不等式，我们就称之为双连不等式，求解双连不等式的方法一：转化为不等式组求解，即 ${\begin{array}{l} 2 < 2 x + 1 \\ 2 x + 1 < 3 \end{array}$ ，解不等式组，得 $\frac{1}{2} < x < 1$ ；方法二：利用不等式性质直接求解，双连不等式的左、中、右同时减去1，得 $1 < 2 x < 2$ ，然后同时除以2，得 $\frac{1}{2} < x < 1$ ．
根据上述材料解决下列问题：

(1)、请你将双连不等式 $- 5 \leq x - 3 < 4$ 转化为不等式组并求解；

(2)、利用不等式的性质解双连不等式 $2 \geq - 2 x + 3 > - 5$ ；

(3)、已知 $- 3 \leq x \leq - \frac{5}{2}$ ，则 $3 x + 5$ 可取的整数值为．

查看试题解析
24. 白色污染（White Pollution）是人们对难降解的塑料垃圾（多指塑料袋）污染环境现象的一种形象称谓．为了让全校同学感受丢弃塑料袋对环境的影响，小彬随机抽取某小区 $40$ 户居民，记录了这些家庭某个月丢弃塑料袋的数量（单位：个）：
29 39 35 39 39 27 33 35 31 31 32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38 29 39 35 33 39 39 38 42 37 32
请根据上述数据，解答以下问题：
分组
划记
频数
A：25-30
____
____
B：30~35
14
C：35~40
____
____
D：40~45
4
合计
/
40

(1)、小彬按“组距为 $5$ ”列出了如下的频数分布表（每组数据含最小值），请将表中空缺的部分补充完整，并补全频数分布直方图；

(2)、根据（1）中的直方图可以看出，这 $40$ 户居民家这个月丢弃塑料袋的个数在组的家庭最多；（填分组序号）

(3)、根据频数分布表，小彬又画出了图所示的扇形统计图．请将统计图中各组占总数的百分比填在图中；

(4)、若该小区共有 $1000$ 户居民家庭，请你估计每月丢弃的塑料袋数量不小于 $30$ 个的家庭个数．

查看试题解析
25. 小明为练习书法，去商店购买书法用品，购买发票上有部分信息不慎被墨汁污染导致无法识别，如表所示．
名称
单价（元）
数量
金额（元）
墨水
15
■（瓶）
■
毛笔
40
■（支）
■
字帖
■
2（本）
90
总计
5（件）
185
请解答下列问题：

(1)、小明购买墨水和毛笔各多少？

(2)、若小明再次购买墨水和字帖两种用品共花费150元，则有哪几种不同的购买方案？

查看试题解析
26. 如图1，已知 $∠ E F H = 90 °$ ，点 $A$ ， $C$ 分别在射线 $F E$ 和 $F H$ 上，在 $∠ E F H$ 内部作射线 $A B$ ， $C D$ ，使 $A B$ 平行于 $C D$ ．

(1)、如图1，若 $F A B = 150 °$ ，求 $∠ H C D$ 的度数；

(2)、小颖发现，在 $∠ E F H$ 内部，无论 $F A B$ 如何变化， $∠ F A B - ∠ H C D$ 的值始终为定值，请你结合图2求出这一定值；

(3)、①如图3，把图1中的 $∠ E F H = 90 °$ 改为 $∠ E F H = 120 °$ ，其他条件不变，请直接写出 $∠ F A B$ 与 $∠ H C D$ 之间的数量关系；
②如图4，已知 $∠ E F G + ∠ F G C = α$ ，点 $A$ ， $C$ 分别在射线 $F E$ ， $G H$ 上，在 $∠ E F G$ 与 $∠ F G H$ 内部作射线 $A B$ ， $C D$ ，使 $A B$ 平行于 $C D$ ，请直接写出 $∠ F A B$ 与 $∠ H C D$ 之间的数量关系．

查看试题解析

分组	划记	频数
A：25-30	____	____
B：30~35		14
C：35~40	____	____
D：40~45		4
合计	/	40

名称	单价（元）	数量	金额（元）
墨水	15	■（瓶）	■
毛笔	40	■（支）	■
字帖	■	2（本）	90
总计		5（件）	185