河北省保定市清苑区2021-2022学年七年级下学期期末数学试题
试卷更新日期:2023-04-28 类型:期末考试
一、单选题
-
1. 下列北京冬奥会运动标识图案是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 下列结论中,正确的是( )A、相等的角是对顶角 B、在同一平面内,不相交的两条线段平行 C、一个角的余角比它的补角小90° D、过一点有且只有一条直线与已知直线平行4. 下列事件是必然事件的是( ).A、随意掷两个均匀的骰子,朝上面的点数之和为6 B、抛一枚硬币,正面朝上 C、3个人分成两组,一定有2个人分在一组 D、打开电视,正在播放动画片5. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 下列结论中,正确的是( )A、相等的角是对顶角 B、在同一平面内,不相交的两条线段平行 C、一个角的余角比它的补角小90° D、过一点有且只有一条直线与已知直线平行4. 下列事件是必然事件的是( ).A、随意掷两个均匀的骰子,朝上面的点数之和为6 B、抛一枚硬币,正面朝上 C、3个人分成两组,一定有2个人分在一组 D、打开电视,正在播放动画片5. 如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是( )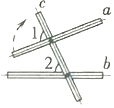 A、10° B、20° C、50° D、70°6. 如图,小刀的刀片上下是平行的,刀柄外形是一个直角梯形(下底挖去一个小半圆,则的度数为( )
A、10° B、20° C、50° D、70°6. 如图,小刀的刀片上下是平行的,刀柄外形是一个直角梯形(下底挖去一个小半圆,则的度数为( )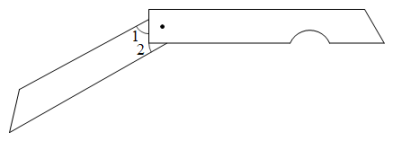 A、 B、 C、 D、不能确定7. 用小数表示为( )A、 B、0.0413 C、0.00413 D、0.0004138. 墨迹覆盖了等式“”中的运算符号,则覆盖的是( )A、× B、÷ C、+ D、-9. 如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;最后,他用步测的办法量出自己与E点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定△ABC≌△DFE的理由可以是( )
A、 B、 C、 D、不能确定7. 用小数表示为( )A、 B、0.0413 C、0.00413 D、0.0004138. 墨迹覆盖了等式“”中的运算符号,则覆盖的是( )A、× B、÷ C、+ D、-9. 如图,抗日战争期间,为了炸毁敌人的碉堡,需要测出我军阵地与敌人碉堡的距离.我军战士想到一个办法,他先面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部点B;然后转过身保持刚才的姿势,这时视线落在了我军阵地的点E上;最后,他用步测的办法量出自己与E点的距离,从而推算出我军阵地与敌人碉堡的距离,这里判定△ABC≌△DFE的理由可以是( ) A、SSS B、SAS C、ASA D、AAA10. 某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )
A、SSS B、SAS C、ASA D、AAA10. 某小组做“当试验次数很大时,用频率估计概率”的试验时,统计了某一结果出现的频率,表格如下,则符合这一结果的试验最有可能是( )次数
100
200
300
400
500
600
700
800
900
1000
频率
0.60
0.30
0.50
0.36
0.42
0.38
0.41
0.39
0.40
0.40
A、掷一个质地均匀的骰子,向上的面点数是“6” B、掷一枚一元的硬币,正面朝上 C、不透明的袋子里有2个红球和3个黄球,除颜色外都相同,从中任取一球是红球 D、三张扑克牌,分别是3,5,5,背面朝上洗匀后,随机抽出一张是511. 如图,直线、、相交于点 , 且 , 平分 , 若 , 则的度数为( )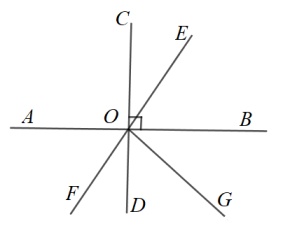 A、 B、 C、 D、无法确定12. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且有两条对称轴,这个位置是( )
A、 B、 C、 D、无法确定12. 图1和图2中所有的小正方形都全等,将图1的正方形放在图2中①②③④的某一位置,使它与原来7个小正方形组成的图形是轴对称图形,并且有两条对称轴,这个位置是( ) A、① B、② C、③ D、④13.
A、① B、② C、③ D、④13.如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式: ①(2a+b)(m+n); ②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b); ④2am+2an+bm+bn,你认为其中正确的有( )
 A、①② B、③④ C、①②③ D、①②③④14. 如图,在△ABC与△DEF中,给出以下六个条件:
A、①② B、③④ C、①②③ D、①②③④14. 如图,在△ABC与△DEF中,给出以下六个条件:⑴AB=DE;⑵)BC=EF;⑶AC=DF;⑷∠A=∠D;⑸∠B=∠E;⑹∠C=∠F,
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )
 A、(1)(5)(2) B、(1)(2)(3) C、(2)(3)(4) D、(4)(6)(1)15. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、
A、(1)(5)(2) B、(1)(2)(3) C、(2)(3)(4) D、(4)(6)(1)15. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、 B、
B、 C、
C、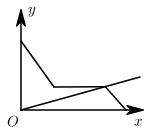 D、
D、 16. 如图1,点是的中点,点在上,动点以每秒的速度沿图1()的边线运动,运动路径为: , 相应的的面积关于运动时间的图象如图2.若 , 有下列结论:
16. 如图1,点是的中点,点在上,动点以每秒的速度沿图1()的边线运动,运动路径为: , 相应的的面积关于运动时间的图象如图2.若 , 有下列结论:①图1中的长是;
②图2中的表示第4秒时,的值为;
③图2中的点表示第12秒时,的值为 .
其中,正确结论的个数是( )
 A、0个 B、1个 C、2个 D、3个
A、0个 B、1个 C、2个 D、3个二、填空题
-
17. 数学课上,老师要求同学们利用三角板画两条平行线.如图,小华的画法:①将含角三角尺的最长边与直线重合,用虚线作出一条最短边所在直线;②再次将含角三角尺的最短边与虚线重合,画出最长边所在直线 , 则 . 你认为他画图的依据是 .
 18. 已知 , 则代数式的值是 .19. 如图①,一种圆环的外圆直径是8cm,环宽1cm.如图②,若把2个这样的圆环扣在一起并拉紧,则其长度为cm;如图③,若把x个这样的圆环扣在一起并拉紧,其长度为ycm,则y与x之间的关系式是 .
18. 已知 , 则代数式的值是 .19. 如图①,一种圆环的外圆直径是8cm,环宽1cm.如图②,若把2个这样的圆环扣在一起并拉紧,则其长度为cm;如图③,若把x个这样的圆环扣在一起并拉紧,其长度为ycm,则y与x之间的关系式是 .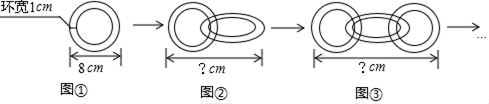
三、解答题
-
20. 计算(1)、;(2)、(用乘法公式计算);(3)、;(4)、先化简,再求值: , 其中 , .21. 把下面的推理过程补充完整,并在括号内注明理由.
如图,已知 , .
试说明: .

解:(已知),
( ).
( ).
又(已知),
( )( ).
( )。
( ).
22. 对于任意四个有理数 , , , , 都可以组成两个有理数对与 . 我们规定: . 例如: .根据上述规定解决下列问题:
(1)、;(2)、计算;(3)、当 , 时,求的值.23. 在一个不透明的袋子中装有个红球和个黄球,这些球除颜色外都相同,将袋子中的球充分摇匀后,随机摸出一球.
(1)、分别求出摸出的球是红球和黄球的概率.(2)、为了使摸出两种球的概率相同,再放进去个同样的红球或黄球,那么这个球中红球和黄球的数量分别应是多少?24. 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有线段和直线 , 点 , , , 均在小正方形的顶点上. (1)、在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点 , 点的对称点为点;(2)、利用网格计算四边形的面积.25. 疫情期间,全民检测,人人有责,幸福小区某时段进行核酸检测,居民有序排队入场,医务人员开始检测后,现场排队等待检测人数(人)与时间(分钟)之间的关系式为 , 用表格表示为:
(1)、在方格纸中画四边形(四边形的各顶点均在小正方形的顶点上),使四边形是以直线为对称轴的轴对称图形,点的对称点为点 , 点的对称点为点;(2)、利用网格计算四边形的面积.25. 疫情期间,全民检测,人人有责,幸福小区某时段进行核酸检测,居民有序排队入场,医务人员开始检测后,现场排队等待检测人数(人)与时间(分钟)之间的关系式为 , 用表格表示为:时间/分钟
0
1
2
3
4
5
6
…
等待检测人数/人
40
50
60
70
80
90
100
医务人员已检测的总人数(人)与时间(分钟)之间的关系如图所示:
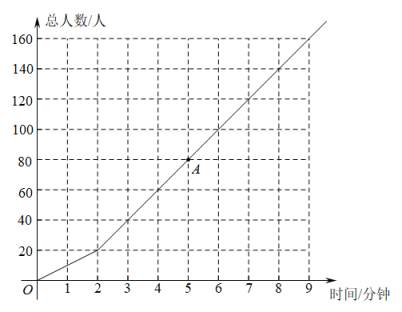 (1)、图中表示的自变量是 , 因变量是;(2)、图中点表示的含义是 ;(3)、在医务人员开始检测4分钟时,现场排队等待检测的人数有 人;(4)、关系式中,的值为;(5)、医务人员开始检测分钟后,现场排队等待检测人数与医务人员已检测的总人数相同;(6)、如果该小区共有居民1200人,那么医务人员全部检测完该小区居民共需分钟.26. 如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)、图中表示的自变量是 , 因变量是;(2)、图中点表示的含义是 ;(3)、在医务人员开始检测4分钟时,现场排队等待检测的人数有 人;(4)、关系式中,的值为;(5)、医务人员开始检测分钟后,现场排队等待检测人数与医务人员已检测的总人数相同;(6)、如果该小区共有居民1200人,那么医务人员全部检测完该小区居民共需分钟.26. 如图,已知△ABC中,AB=AC=6cm,BC=4cm,点D为AB的中点.如果点P在线段BC上以1cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.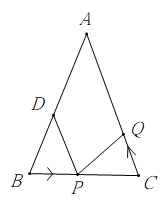 (1)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
(1)、若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?