人教版初中数学几何辅助线进阶训练——遇角平分线做垂线(不含相似八九年级适用)
试卷更新日期:2023-04-27 类型:复习试卷
一、一阶段(较易)
-
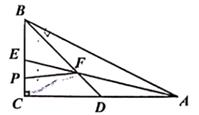
1. 如图,在中, , 平分 , , , 那么点到直线的距离是( )
 A、 B、 C、 D、2. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( )
A、 B、 C、 D、2. 如图,的角平分线 , 交于点 , , 的面积为16,四边形的面积为5,则的面积为( ) A、5 B、5.5 C、6 D、73. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.
A、5 B、5.5 C、6 D、73. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是.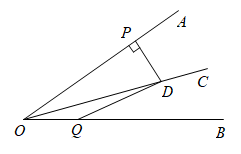 4. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为.
4. 如图,在中,是边上的高,平分 , 交于点E, , 若的面积为9,则的长为. 5. 如图,在四边形中, , , , , 则点到边的距离等于 .
5. 如图,在四边形中, , , , , 则点到边的距离等于 . 6. 如图,中, , 平分交于点P,若 , , 则的面积是( )
6. 如图,中, , 平分交于点P,若 , , 则的面积是( ) A、 B、 C、 D、7. 如图所示,点O是内一点,平分 , 于点D,连接 , 若 , 则的面积是 .
A、 B、 C、 D、7. 如图所示,点O是内一点,平分 , 于点D,连接 , 若 , 则的面积是 . 8. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为.
8. 如图,平分 , 于点C,且 , 已知点A到y轴的距离是4,那么点A的坐标为. 9. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .
9. 如图,在△ABC中,CD是边AB上的高,BE平分∠ABC,交CD于点E,BC=5,若△BCE的面积为5,则ED的长为 .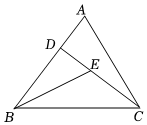 10. 如图, 是 的角平分线, 于点E, , , ,则 的长是( )
10. 如图, 是 的角平分线, 于点E, , , ,则 的长是( )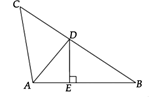 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、二阶段(中等)
-
11. 如图,在四边形中, , 平分 , , 则的面积是( )
 A、6 B、8 C、10 D、1212. 如图,在四边形中, , O为上的一点,且平分平分.求证:
A、6 B、8 C、10 D、1212. 如图,在四边形中, , O为上的一点,且平分平分.求证: (1)、.(2)、.13. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
(1)、.(2)、.13. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.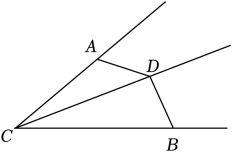 14. 如图,是的角平分线, , 垂足为F, , 和的面积分别为27和14,则的面积为 .
14. 如图,是的角平分线, , 垂足为F, , 和的面积分别为27和14,则的面积为 . 15. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )
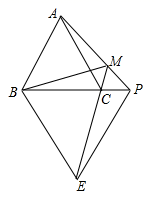
15. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EFBC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°∠A,②∠EBO∠AEF,③∠DOC+∠OCB=90°,④设OD=m,AE+AF=n,则S△AEF . 其中正确的结论有( )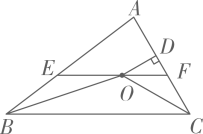 A、1个 B、2个 C、3个 D、4个16. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( )
A、1个 B、2个 C、3个 D、4个16. 如图,在△ABC中,若分别以AB、AC为边作△ABD和△ACE,且∠DAB=∠CAE=α,AD=AB,AC=AE,DC、BE交于点P,连接AP,则∠APC的度数为( ) A、90°﹣α B、90°+α C、90°﹣α D、90°+α17. 已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF.
A、90°﹣α B、90°+α C、90°﹣α D、90°+α17. 已知:如图,在△ABC中,AB=AC,在△ADE中,AD=AE,且∠BAC=∠DAE,连接BD,CE交于点F,连接AF. (1)、求证:△ABD≌△ACE;(2)、求证:FA平分∠BFE.18. 如图,在中,是的平分线,延长至点E,使 , 连接 , 若 , 的面积为1,则的面积是.
(1)、求证:△ABD≌△ACE;(2)、求证:FA平分∠BFE.18. 如图,在中,是的平分线,延长至点E,使 , 连接 , 若 , 的面积为1,则的面积是. 19. 如图1,在△ABC中,BO⊥AC于点O,AO=BO=3,OC=1,过点A作AH⊥BC于点H,交BO于点P.
19. 如图1,在△ABC中,BO⊥AC于点O,AO=BO=3,OC=1,过点A作AH⊥BC于点H,交BO于点P.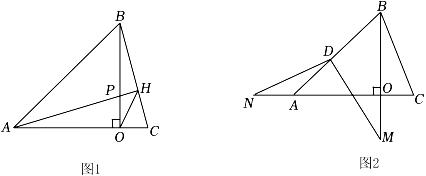 (1)、求线段OP的长度;(2)、连接OH,求∠AHO的度数;(3)、如图2,若点D为AB的中点,点M为线段BO延长线上一动点,连接MD,过点D作DN⊥DM交线段OA延长线于N点,则S△BDM-S△ADN的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.20. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)、求线段OP的长度;(2)、连接OH,求∠AHO的度数;(3)、如图2,若点D为AB的中点,点M为线段BO延长线上一动点,连接MD,过点D作DN⊥DM交线段OA延长线于N点,则S△BDM-S△ADN的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.20. 如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.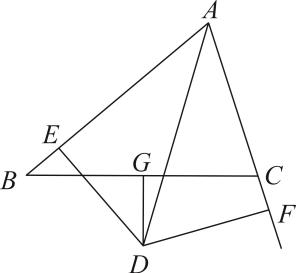 (1)、求证:BE=CF;(2)、如果AB=5,AC=3,求BE的长.
(1)、求证:BE=CF;(2)、如果AB=5,AC=3,求BE的长.三、三阶段(较难)
-
21. 综合与实践:
问题情境:已知是的平分线,P是射线上的一点,点C,D分别在射线 , 上,连接 .
 (1)、初步探究:如图1,当 , 时,与的数量关系是;(2)、深入探究:如图2,点C,D分别在射线 , 上运动,且 , 当时,与在(1)中的数量关系还成立吗?请说明理由;(3)、拓展应用:如图3,如果点C在射线上运动,且 , 当时,点D落在了射线的反向延长线上,若点P到的距离为3, , 求的长(直接写出答案).22. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )
(1)、初步探究:如图1,当 , 时,与的数量关系是;(2)、深入探究:如图2,点C,D分别在射线 , 上运动,且 , 当时,与在(1)中的数量关系还成立吗?请说明理由;(3)、拓展应用:如图3,如果点C在射线上运动,且 , 当时,点D落在了射线的反向延长线上,若点P到的距离为3, , 求的长(直接写出答案).22. 如图,等边中,、分别为、边上的点, , 连接、交于点 , 、的平分线交于边上的点 , 与交于点 , 连接下列说法:≌;;;;其中正确的说法有( )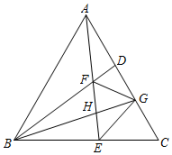 A、4个 B、3个 C、2个 D、1个23. 如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( )
A、4个 B、3个 C、2个 D、1个23. 如图,已知△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC.①BD=CE;②∠AHC=60°;③FC=CG;④S△CBD=S△CGH;其中说法正确的有( ) A、1个 B、2个 C、3个 D、4个24. 如图,在Rt△ABC中,∠C=90°,两锐角的角平分线交于点P,点E、F分别在边BC、AC上,且都不与点C重合,若∠EPF=45°,连接EF,当AC=6,BC=8,AB=10时,则△CEF的周长为 .
A、1个 B、2个 C、3个 D、4个24. 如图,在Rt△ABC中,∠C=90°,两锐角的角平分线交于点P,点E、F分别在边BC、AC上,且都不与点C重合,若∠EPF=45°,连接EF,当AC=6,BC=8,AB=10时,则△CEF的周长为 . 25. 如图,已知点B(-2,0),C(2,0),A为y轴正半轴上一点,点D为第二象限内的一个动点,M在BD的延长线上,CD交AB于点F,且∠ABD=∠ACD.
25. 如图,已知点B(-2,0),C(2,0),A为y轴正半轴上一点,点D为第二象限内的一个动点,M在BD的延长线上,CD交AB于点F,且∠ABD=∠ACD. (1)、求证:∠BDC=∠BAC;(2)、求证:DA平分∠CDM;(3)、若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数?26. 如图1,在 中, , 分别是 和 的角平分线, 和 相交于D点.
(1)、求证:∠BDC=∠BAC;(2)、求证:DA平分∠CDM;(3)、若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数?26. 如图1,在 中, , 分别是 和 的角平分线, 和 相交于D点. (1)、求证: 平分 ;(2)、如图2,过F作 于点P,连接 ,若 , ,求证: ;(3)、如图3,若 ,求证: .27. 如图,△ABC中,AB=AC,∠BAC+∠BDC=180°.
(1)、求证: 平分 ;(2)、如图2,过F作 于点P,连接 ,若 , ,求证: ;(3)、如图3,若 ,求证: .27. 如图,△ABC中,AB=AC,∠BAC+∠BDC=180°.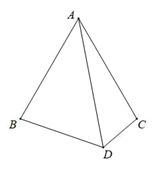
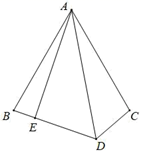 (1)、求证:AD为∠BDC的平分线;(2)、若∠DAE= ∠BAC,且点E在BD上,直接写出BE、DE、DC三条线段之间的等量关系 .
(1)、求证:AD为∠BDC的平分线;(2)、若∠DAE= ∠BAC,且点E在BD上,直接写出BE、DE、DC三条线段之间的等量关系 .