吉林省长春市朝阳区2022年中考一模——数学试卷

试卷更新日期：2023-04-27 类型：中考模拟

进入出卷网下载

一、选择题(每小题3分，共24分)

1. 在－2，0，1， $\sqrt{2}$ 这四个数中，最小的数是（）

A、－2 B、0 C、1 D、 $\sqrt{2}$

查看试题解析
2. 北京冬奥会吉祥物“冰墩墩”深受大家喜爱．在冬奥会期间，某个“冰墩墩”的视频播放量超过256万次，2 560 000这个数用科学记数法表示为（）

A、256×10⁴ B、25.6×10⁵ C、2.56×10⁶ D、0.256×10⁷

查看试题解析
3. 下图是由5个大小相同的正方体组成的立体图形，其俯视图是（）

A、 B、 C、 D、

查看试题解析
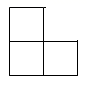4. 若点A (2，6)关于x轴对称后得到点B，则点B的坐标为（）

A、(-2，6) B、(2，-6) C、(6，-2) D、(-6，2)

查看试题解析
5. 关于x的一元二次方程x²-4x+m=0没有实数根，则m的值可能是（）

A、-2 B、0 C、3 D、5

查看试题解析
6. 如图，已知A、C两点的距离为5米，∠A=α，则树高BC为（）

A、5sinα米 B、5cosα米 C、5tanα米 D、 $\frac{5}{t a n α}$ 米

查看试题解析
7. 如图，在Rt△ABC中，∠C=90°，以顶点B为圆心，适当长度为半径画弧，分别交AB、BC于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线BP交边AC于点D．若CD=2 $\sqrt{3}$ ， AB=12，则△ABD的面积为（）

A、6 $\sqrt{3}$ B、12 $\sqrt{3}$ C、18 $\sqrt{3}$ D、24 $\sqrt{3}$

查看试题解析
8. 如图，在平面直角坐标系中，菱形ABCD位于第一象限，且对角线AC、BD所在的直线与坐标轴垂直，点A的坐标为(1，4)，点D的坐标为(2，1)．若双曲线y= $\frac{k}{x}$ 与菱形ABCD有公共点，则k的取值范围为（）

A、2≤k≤12 B、2≤k≤ $\frac{55}{4}$ C、2≤k≤14 D、2≤k≤ $\frac{169}{12}$

查看试题解析

二、填空题(每小题3分，共18分)

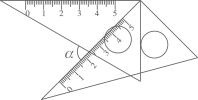
9. 分解因式：2a-a²=

查看试题解析
10. 不等式组 ${\begin{cases} x + 1 > 0 \\ 2 x \leq 3 \end{cases}$ 的解集为

查看试题解析
11. 如图，将一个含有30°角的直角三角板绕着直角顶点逆时针旋转45°，则∠α的大小为

查看试题解析
12. 如图，AB是00的直径，CD切⊙O于点C．若∠BCD=50°，则∠ABC的大小为

查看试题解析
13. 如图，在平行四边形ABCD中，∠BAC=60°，∠ABC=100°，BC=6，点E为BC的中点，以点E为圆心，线段BE的长为半径画弧，交AC于点F，则阴影部分的面积为． (结果保留π)

查看试题解析
14. 如图，在平面直角坐标系中，抛物线y=-x²+2mx+m-2(m为常数，且m>0)与直线y=2交于A、B两点．若AB=2，则m的值为

查看试题解析

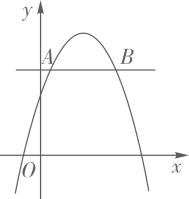
三、解答题(本大题10小题，共78分)

15. 先化简，再求值：x(3-x)+(x+1)(x-1)，其中x= $- \frac{1}{3}$

查看试题解析
16. 一个不透明的口袋中有三个小球上面分别标有数字2、3、4，每个小球除数字不同外其余均相同．

(1)、若融融同学从口袋中随机摸出一个小球，小球上的数字是奇数的概率是

(2)、若融融同学从口袋中随机摸出一个小球，记下数字后放回，再随机摸出一个小球，记下数字．请用画树状图(或列表)的方法，求两次摸出的小球上的数字都是偶数的概率．

查看试题解析
17. 为支持“抗疫防病”工作，某口罩厂由甲、乙两车间承制防护型口罩，已知乙车间每天生产口罩数量是甲车间每天生产口罩数量的1.5倍．如果两车间各自生产600万只防护型口罩，乙车间比甲车间少用4天．求甲车间每天生产这种防护型口罩的数量．

查看试题解析
18. 如图，在四边形ABCD中，AB∥CD，BC=DC，CE平分∠BCD交边AB于点E，连结DE．

(1)、求证：四边形BCDE是菱形．

(2)、连结BD，若BD=AD=4，tan∠A= $\frac{1}{2}$ ，则CE的长为

查看试题解析
19. 图①、图2．图③均是5×5的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，线段AB的端点均在格点上．只用无刻度的直尺，分别在给定的网格中，以AB为边画三角形．按下列要求作图：

(1)、在图①中，画一个等腰△ABC，使其面积为3．

(2)、在图②中，画一个直角三角形△ABD，使其面积为 $\frac{10}{3}$

(3)、在图③中，画一个△ABE，使其面积为 $\frac{15}{4}$ ，且∠BAE=45°．

查看试题解析
20. 今年是中国共产主义青年团成立100周年，某校组织七、八年级开展了以“请党放心、强国有我”为主题的团史知识竞赛．为了解学生对团史知识掌握的整体情况，分别从七、八年级各随机抽取20名学生的竞赛成绩(满分： 100 分)进行整理、描述和分析，给出以下部分信息：
a．七年级20名学生竞赛成绩的频数分布表和频数分布直方图：
表1七年级20名学生竞赛成绩的频数分布表
成绩m(分)
频数（人）
频率
50≤m< 60
a
0.05
60≤m< 70
b
c
70≤m< <80
3
0.15
80≤m<90
8
0.40
90≤m≤100
6
0.30
合计
20
1.00
表2七年级20名学生竞赛成绩的频数分布直方图
b．七年级竞赛成绩在80≤m<90一组的具体成绩为：83，84，86，87，88，89，89，89．
c．七、八年级竞赛成绩的统计数据如下表(表3)所示：
年级
平均分
中位数
众数
七年级
83.7
m
89
八年级
84.2
85
85
根据以上信息，解答下列问题：

(1)、在表1中，a=；在表3中，m=

(2)、补全表2中七年级20名学生竞赛成绩的频数分布直方图．

(3)、在这次竞赛活动中，某学生的竞赛成绩是86分，在他所属的样本中位于中等偏上水平，那么这个学生是年级的学生，理由是

(4)、若竞赛成绩不低于85分为优秀，根据统计结果，估计七年级600名学生中竞赛成绩优秀的人数．

查看试题解析
21. 作为中国四大传统节日之一的端午节即将到来，某食品厂“为了慰问老红军，临时抽调甲、乙两个车间同时开始加工粽子，加工一段时间后，甲车间的设备出现故障停产一段时间，乙车间继续加工，甲车间维修好设备后，继续按照原来的工作效率加工，从工作开始到加工完这批粽子，乙车间连续工作10小时，甲、乙两车间各自加工粽子的数量y (个)与加工时间t (时)之间的函数图象如图所示．

(1)、乙车间每小时加工个粽子：a的值为

(2)、求甲车间维修完设备后，y与x之间的函数关系式．

(3)、当甲、乙两车间各自加工的粽子的数量相差50个时，直接写出t的值．

查看试题解析
22. [教材呈现]华师版八年级上册教材第69页的部分内容．

例4如图13.2.13，在△ABC中，D是边BC的中点，过点C画直线CE，使CE∥AB，交AD的延长线于点E．求证：AD=ED．

证明：∵CE∥AB (已知)，

(1)、请根据教材内容，结合图①，补全证明过程．

(2)、[结论应用]如图②，在平行四边形ABCD中，点E是边AD的中点，连结CE，线段CE与BA边的延长线交于点F，点P、Q分别在线段CE，EF上，且CP=FQ．
求证：四边形APDO是平行四边形，

(3)、如图③在矩形ABCD中，AB=2，AD =4，分别取AB、CD边的中点E、F，连结EF，经过线段EF中点O任意作一条直线l，作点B关于直线l的对称点P，连结PE、PO、PF，过点E作PF的平行线交PO的延长线于点Q，连结FQ，得到四边形PEQF．则四边形PEQF面积的最大值为

查看试题解析
23. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，Q为AB的中点．动点P从点A出发沿折线AC--CB以每秒2个单位长度的速度运动，连结PQ，以PQ为边构造正方形PMNQ且边MN与点B始终在边PQ同侧．设点P的运动时间为t秒(>0)．

(1)、线段AB的长为

(2)、当点P在边AC上运动时，线段CP的长为 ▲ (用含t的代数式表示) ．
①当正方形PMNQ与△ABC重叠部分图形是正方形时，求t的取值范围．
②当边MN的中点落在△ABC的边上时，求正方形PMNQ的面积．

(3)、当点P不与点C重合时，作点C关于直线PQ的对称点C'当PC'⊥AB时，直接写出t的值．

查看试题解析
24. 在平面直角坐标系中，抛物线y= $\frac{1}{a}$ x²-2x+2(a为常数，且af0)的顶点为M，与y轴交于点A．

(1)、点A的坐标为

(2)、当a>0，且-1≤x≤4时，若函数y= $\frac{1}{a}$ x²-2x+2的最大值为5，求a的值．

(3)、若抛物线与直线y=4有公共点，将抛物线在直线y=4下方的部分沿直线y=4翻折，其他部分保持不变，得到新的图象G₁ ．当图象G，上存在两个点到直线y=4的距离为3时，求a的取值范围．

(4)、当直线x=a+2(a>-2)与抛物线交于点B，抛物线在A、B之间的部分(包括A、B两点)记为图象G₂ ，以AB为对角线构造矩形ACBD，且矩形的边所在的直线垂直于坐标轴．当过顶点M和图象G₂的最高点的直线将矩形ACBD的面积分为1：5两部分时，直接写出a的值．

查看试题解析

成绩m(分)	频数（人）	频率
50≤m< 60	a	0.05
60≤m< 70	b	c
70≤m< <80	3	0.15
80≤m<90	8	0.40
90≤m≤100	6	0.30
合计	20	1.00

年级	平均分	中位数	众数
七年级	83.7	m	89
八年级	84.2	85	85