人教版初中数学几何辅助线进阶训练——构造等腰三角形(不含相似)
试卷更新日期:2023-04-27 类型:复习试卷
一、阶段一(较易)
-
1. 如图,在 ▱ ABCD,点F是BC上的一点,连接AF,AE平分∠FAD,交CD于中点E,连接EF.若∠FAD=60°,AD=5,CF=3,则EF= .
 2. 如图,▱ABCD中,对角线AC、BD相交于O,过点O作OE⊥AC交AD于E,若AE=4,DE=3,AB=5,则AC的长为( )
2. 如图,▱ABCD中,对角线AC、BD相交于O,过点O作OE⊥AC交AD于E,若AE=4,DE=3,AB=5,则AC的长为( ) A、 B、 C、 D、3. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
A、 B、 C、 D、3. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长. 4. 如图,中,平分 , , 垂足为D,E为中点,若 , , 则的长为 .
4. 如图,中,平分 , , 垂足为D,E为中点,若 , , 则的长为 . 5. 如图,在中, , , , 点D在外,连接、 , 点E是的中点, , , 则线段的长 .
5. 如图,在中, , , , 点D在外,连接、 , 点E是的中点, , , 则线段的长 . 6. 如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点.求证:FM⊥DE。
6. 如图,△ABC中,BD、CE是△ABC的两条高,点F、M分别是DE、BC的中点.求证:FM⊥DE。 7. 如图,△ABC中,∠ACB=90°,点D是边BC上一点,DE⊥AB于点E,点F是线段AD的中点,连接EF、CF;
7. 如图,△ABC中,∠ACB=90°,点D是边BC上一点,DE⊥AB于点E,点F是线段AD的中点,连接EF、CF; (1)、求证:EF=CF;(2)、若∠BAC=45°,AD=6,求C、E两点间的距离.8. 如图,在中, , , , 其中 , , , ( )
(1)、求证:EF=CF;(2)、若∠BAC=45°,AD=6,求C、E两点间的距离.8. 如图,在中, , , , 其中 , , , ( ) A、 B、 C、 D、9. 如图,P为△ABC边BC上的一点,且PC=2PB,已知∠ABC=45°,∠APC=60°,则∠ACB的度数是 °.
A、 B、 C、 D、9. 如图,P为△ABC边BC上的一点,且PC=2PB,已知∠ABC=45°,∠APC=60°,则∠ACB的度数是 °. 10. 如图,D为内一点,平分 , , , 若 , . 则的长为( )
10. 如图,D为内一点,平分 , , , 若 , . 则的长为( )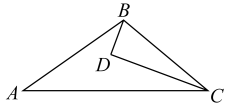 A、1 B、 C、2 D、11. 如图,在△ABC中,BP平分∠ABC,于点P,连接PC,若△PAB的面积为 , △PBC的面积为 , 则△PAC的面积为( ).
A、1 B、 C、2 D、11. 如图,在△ABC中,BP平分∠ABC,于点P,连接PC,若△PAB的面积为 , △PBC的面积为 , 则△PAC的面积为( ). A、2 B、2.5 C、3 D、4
A、2 B、2.5 C、3 D、4二、阶段二(中等)
-
12. 如图,在中,∠BAC=120°,点D为BC的中点,点E是AC上的一点,且 . 若 , 则AB的长为( )
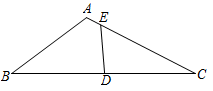 A、 B、4 C、 D、613. 如图,四边形ABCD中,∠DAB=∠BCD=90°,对角线AC=8,点E,F,O分别为AD,AB,BD的中点,且EF=5,则点O到AC的距离为 .
A、 B、4 C、 D、613. 如图,四边形ABCD中,∠DAB=∠BCD=90°,对角线AC=8,点E,F,O分别为AD,AB,BD的中点,且EF=5,则点O到AC的距离为 . 14. 如图,在中, , 是斜边上的中点,、分别是、边上的点,且
14. 如图,在中, , 是斜边上的中点,、分别是、边上的点,且 (1)、若 , , 求四边形的面积.(2)、求证:.15. 如图,正方形中,P为边上一点,点E与B关于直线对称,射线与的延长线相交于点F.若 , , 则的长为 .
(1)、若 , , 求四边形的面积.(2)、求证:.15. 如图,正方形中,P为边上一点,点E与B关于直线对称,射线与的延长线相交于点F.若 , , 则的长为 . 16. 如图,在中, , 是边上的高线,过点D作交于点E.
16. 如图,在中, , 是边上的高线,过点D作交于点E. (1)、求证:是等腰三角形;(2)、连结交于点H,若 , 求的长.17. 如图,四边形ABCD是正方形,点P是线段AB的延长线上一点,点M是线段AB上一点,连接DM,以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N,过点C作CEMN交AD于E,连接EM,CN,DN.
(1)、求证:是等腰三角形;(2)、连结交于点H,若 , 求的长.17. 如图,四边形ABCD是正方形,点P是线段AB的延长线上一点,点M是线段AB上一点,连接DM,以点M为直角顶点作MN⊥DM交∠CBP的角平分线于N,过点C作CEMN交AD于E,连接EM,CN,DN.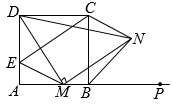 (1)、求证:DM=MN;(2)、求证:EMCN.18. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )
(1)、求证:DM=MN;(2)、求证:EMCN.18. 如图,在中, , , 平分 , , 为边的垂直平分线且分别交、于点、 , 若 , , 则的长是( )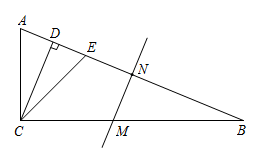 A、2 B、 C、 D、19. 已知:在等边中,点是边所在直线上的一个动点(与、两点均不重合),点在的延长线上,且.
A、2 B、 C、 D、19. 已知:在等边中,点是边所在直线上的一个动点(与、两点均不重合),点在的延长线上,且.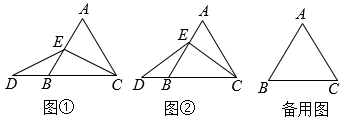 (1)、如图①,当是边的中点时,求证:;(2)、如图②,当是线段边上任意一点时,(1)中的结论是否一定成立?请说明理由;(3)、若点是线段的延长线上任一点, , , , 求的长.20. 如图,在△ABC中,AB=AC=2 , AD是边BC上的高线,过点D作DE∥AC交AB于点E.
(1)、如图①,当是边的中点时,求证:;(2)、如图②,当是线段边上任意一点时,(1)中的结论是否一定成立?请说明理由;(3)、若点是线段的延长线上任一点, , , , 求的长.20. 如图,在△ABC中,AB=AC=2 , AD是边BC上的高线,过点D作DE∥AC交AB于点E. (1)、求证:△ADE是等腰三角形;(2)、连结CE交AD于点H,若∠DCE=45°,求EH的长.
(1)、求证:△ADE是等腰三角形;(2)、连结CE交AD于点H,若∠DCE=45°,求EH的长.三、阶段三(较难)
-
21. 请阅读下列材料,并完成相应的任务.
三等分角是古希腊三大几何问题之一.如图(1),任意∠ABC可被看作是矩形BCAD的对角线BA与边BC的夹角,以B为端点的射线BF交CA于点 , 交DA的延长线于点F.若 , 则射线BF是∠ABC的一条三等分线.
证明:如图(2),取EF的中点G,连接AG,∵四边形BCAD是矩形,∴ , ADBC.在Rt△AEF中,点G是EF的中点,∴……
 (1)、任务一:上面证明过程中得出“”的依据是;(2)、任务二:完成材料证明中的剩余部分;(3)、任务三:如图(3),在矩形ABCD中,对角线AC的延长线与∠CBE的平分线交于点F,若 , , 请直接写出BF的长.22.(1)、【阅读材料】如图①,四边形ABCD中, , 点E,F分别在上,若 , 求证:.
(1)、任务一:上面证明过程中得出“”的依据是;(2)、任务二:完成材料证明中的剩余部分;(3)、任务三:如图(3),在矩形ABCD中,对角线AC的延长线与∠CBE的平分线交于点F,若 , , 请直接写出BF的长.22.(1)、【阅读材料】如图①,四边形ABCD中, , 点E,F分别在上,若 , 求证:.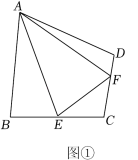 (2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)
(2)、【解决问题】如图②,在某公园的同一水平面上,四条道路围成四边形.已知 , 道路上分别有景点M,N,且m,若在M,N之间修一条直路,则路线M→N的长比路线M→A→N的长少几m?(结果取整数,参考数据:)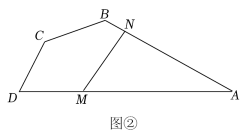 23. 如图
23. 如图 (1)、发现:如图1,点是线段上的一点,分别以 , 为边向外作等边三角形和等边三角形 , 连接 , , 相交于点.
(1)、发现:如图1,点是线段上的一点,分别以 , 为边向外作等边三角形和等边三角形 , 连接 , , 相交于点.①线段与的数量关系为:;的度数为.
②可看作经过怎样的变换得到的?.
(2)、应用:如图2,若点 , , 不在一条直线上,中的结论①还成立吗?请说明理由;(3)、拓展:在四边形中, , , , 若 , , 请直接写出 , 两点之间的距离.24. 请阅读下列材料:已知:如图(1)在中, , 点D、E分别为线段上两动点,若.探究线段三条线段之间的数量关系.小明的思路是:把绕点A顺时针旋转 , 得到 , 连接 , 使问题得到解决.请你参考小明的思路探究并解决下列问题: (1)、猜想三条线段之间存在的数量关系式,直接写出你的猜想;(2)、当动点E在线段上,动点D运动在线段延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)、已知:如图(3),等边三角形中,点D、E在边上,且 , 请你找出一个条件,使线段能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.25.
(1)、猜想三条线段之间存在的数量关系式,直接写出你的猜想;(2)、当动点E在线段上,动点D运动在线段延长线上时,如图(2),其它条件不变,(1)中探究的结论是否发生改变?请说明你的猜想并给予证明;(3)、已知:如图(3),等边三角形中,点D、E在边上,且 , 请你找出一个条件,使线段能构成一个等腰三角形,并求出此时等腰三角形顶角的度数.25.
(1)、【探究发现】(1)如图1,中, , , 点为的中点,、分别为边、上两点,若满足 , 则、、之间满足的数量关系是.(2)、【类比应用】如图2,中, , , 点为的中点,、分别为边、上两点,若满足 , 试探究、、之间满足的数量关系,并说明理由.(3)、【拓展延伸】在中, , , 点为的中点,、分别为直线、上两点,若满足 , , 请直接写出的长.26. 平行四边形中, , 点E在边上,连接. (1)、如图1,交于点G,若平分 , 且 , , 请求出四边形的面积;(2)、如图2,点F在对角线上,且 , 连接 , 过点F作于H,连接 , 求证:.(3)、如图3,线段在线段上运动,点R在边上,连接.若平分 , , , , .请直接写出线段的和的最小值以及此时的面积.27. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )
(1)、如图1,交于点G,若平分 , 且 , , 请求出四边形的面积;(2)、如图2,点F在对角线上,且 , 连接 , 过点F作于H,连接 , 求证:.(3)、如图3,线段在线段上运动,点R在边上,连接.若平分 , , , , .请直接写出线段的和的最小值以及此时的面积.27. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )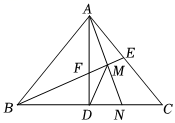 A、2个 B、3个 C、4个 D、5个28. 如图1、在△ABC中,E、D是BC边上的点,且AE是∠BAD的平分线,∠CAE+∠BEA=180°
A、2个 B、3个 C、4个 D、5个28. 如图1、在△ABC中,E、D是BC边上的点,且AE是∠BAD的平分线,∠CAE+∠BEA=180° (1)、若∠CAD=25°,∠C=38°,求∠DAE的度数(2)、当BE=AC时,请猜想线段AB、AD之间的数量关系;并证明你的猜想.(3)、如图2,在(2)的条件下,过D作DF⊥AE,垂足为F,交AB于G,如果 , 请直接写出四边形AFDC的面积.29.(1)、如图1,等腰的直角顶点在正方形的边上,斜边交于点Q,连接 , 求证: . 请利用现在所学的旋转知识,可将旋转到 , 然后通过证明全等三角形来完成证明.
(1)、若∠CAD=25°,∠C=38°,求∠DAE的度数(2)、当BE=AC时,请猜想线段AB、AD之间的数量关系;并证明你的猜想.(3)、如图2,在(2)的条件下,过D作DF⊥AE,垂足为F,交AB于G,如果 , 请直接写出四边形AFDC的面积.29.(1)、如图1,等腰的直角顶点在正方形的边上,斜边交于点Q,连接 , 求证: . 请利用现在所学的旋转知识,可将旋转到 , 然后通过证明全等三角形来完成证明. (2)、如图2,若等腰的直角顶点在正方形的边的延长线上,斜边的延长线交的延长线于点Q,连接 , 猜想线段 , , 满足怎样的数量关系?并证明你的结论;
(2)、如图2,若等腰的直角顶点在正方形的边的延长线上,斜边的延长线交的延长线于点Q,连接 , 猜想线段 , , 满足怎样的数量关系?并证明你的结论; (3)、如图3,中, , , P为内部一点,且 , 则 .
(3)、如图3,中, , , P为内部一点,且 , 则 . 30. 如图,在正方形中,是上一点(不与端点 , 重合),连接过点作的垂线,分别交 , 于点 , 延长到点 , 使得 , 连接 , .
30. 如图,在正方形中,是上一点(不与端点 , 重合),连接过点作的垂线,分别交 , 于点 , 延长到点 , 使得 , 连接 , . (1)、求证:≌;(2)、①若 , 则 ;
(1)、求证:≌;(2)、①若 , 则 ;改变的度数,的度数是否会发生改变?若发生改变,请写出与之间的关系,若不改变,请说明理由;
(3)、如图2,若 , 求与的长.