2023年浙江省绍兴市初中毕业生学业水平测试数学模拟试题(一)
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题(每题4分,共40分)
-
1. 2023的相反数的倒数是( )A、2023 B、-2023 C、 D、2. 中华人民共和国第十四届人民代表大会第一次会议政府工作报告指出:2023年国内生产总值预期增长目标5%左右,城镇新增就业1200万人左右,将1200万用科学记数法表示为( )A、 B、 C、 D、3. 如图是《九章算术》中“堑堵”的立体图形,它的左视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 如图①所示,有6张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“信”的概率是( )
4. 如图①所示,有6张写有汉字的卡片,它们的背面都相同,现将它们背面朝上洗匀后如图2摆放,从中任意翻开一张是汉字“信”的概率是( )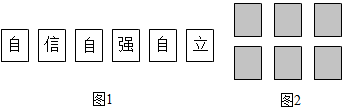 A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,把一块含有角的直角三角板的两个顶点放在直尺的对边上,如果 , 那么的度数是( )
A、 B、 C、 D、5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,把一块含有角的直角三角板的两个顶点放在直尺的对边上,如果 , 那么的度数是( ) A、 B、 C、 D、7. 运用你学习函数的经验,判断以下哪个函数的图象如图所示( )
A、 B、 C、 D、7. 运用你学习函数的经验,判断以下哪个函数的图象如图所示( ) A、 B、 C、 D、8. 如图,在正方形ABCD中,点E,F分别在边DA,AB上,且DE=AF,作AG⊥EF于点H,交BC于点G. 若AB=6,EF∶AG=2∶3,则BG的长为( ).
A、 B、 C、 D、8. 如图,在正方形ABCD中,点E,F分别在边DA,AB上,且DE=AF,作AG⊥EF于点H,交BC于点G. 若AB=6,EF∶AG=2∶3,则BG的长为( ). A、4 B、3 C、2 D、19. 如图,二次函数的图象与x轴相交于 , B两点,对称轴是直线 , 下列说法正确的是( )
A、4 B、3 C、2 D、19. 如图,二次函数的图象与x轴相交于 , B两点,对称轴是直线 , 下列说法正确的是( )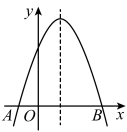 A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,某通信公司就使用宽带网推出了E、F、G三种月收费方式,这三种收费方式每月上网时间与所需费用s(元)的函数关系如图所示,则下列判断错误的是( )
A、 B、当时,y的值随x值的增大而增大 C、点B的坐标为 D、10. 如图,某通信公司就使用宽带网推出了E、F、G三种月收费方式,这三种收费方式每月上网时间与所需费用s(元)的函数关系如图所示,则下列判断错误的是( ) A、每月上网时间不足25h时,选择E方式最省钱 B、每月上网费用为70元时,E方式上网时间比F方式多 C、每月上网时间为35h时,选择F方式最省钱 D、每月上网时间超过80h时,选择G方式最省钱
A、每月上网时间不足25h时,选择E方式最省钱 B、每月上网费用为70元时,E方式上网时间比F方式多 C、每月上网时间为35h时,选择F方式最省钱 D、每月上网时间超过80h时,选择G方式最省钱二、填空题(每空5分,共30分)
-
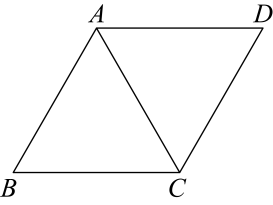
11. 因式分解:m2-4= .12. 在式子中,字母x的取值范围是 .13. 《九章算术》中“盈不足术”有这样的问题:“今有共买羊,人出六,不足四十五;人出八,不足三.问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出6元,则差45元:每人出8元,则差3元.求人数和羊价各是多少?设买羊人数为x人,则根据题意可列方程为 .14. 如图,在边长为12的菱形中, , 连接 , P为或上一点,若 , 则的长为.
 15. 如图,已知是一块含有角的直角三角板,点A是函数的图象上一点,点B是函数的图象上一点,则k的值为 .
15. 如图,已知是一块含有角的直角三角板,点A是函数的图象上一点,点B是函数的图象上一点,则k的值为 .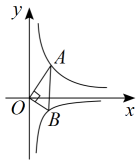 16. 如图,在中, , , 点D和点E分别是边和上的两点,连接 , 将沿折叠,得到 , 点恰好落在的中点处,与交于点F,则下列四个结论:
16. 如图,在中, , , 点D和点E分别是边和上的两点,连接 , 将沿折叠,得到 , 点恰好落在的中点处,与交于点F,则下列四个结论:①;②;③;④ .
其中正确的是(写出正确的结论的序号).

三、解答题(共8题,共80分)
-
17.(1)、计算:(2)、化简:(2x-y)(2x+y)-(2x-y)218. 某校为了了解七年级学生体育测试情况,以七年级(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下的统计图,请你结合图中所给的信息解答下列问题:
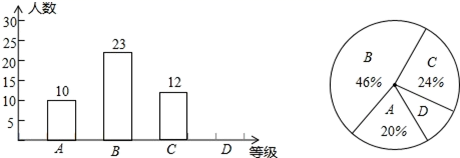
(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)、请把条形统计图补充完整;(2)、扇形统计图中D级所在的扇形的圆心角度数是;(3)、若该校七年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?解:
19. 周老师为锻炼身体一直坚持步行上下班.已知学校到周老师家总路程为2000米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示. (1)、求a的值.(2)、b= ;c= .(3)、求周老师从学校到家的平均速度.20.
(1)、求a的值.(2)、b= ;c= .(3)、求周老师从学校到家的平均速度.20.如图,小明在楼上点A处测量大树的高,在A处测得大树顶部B的仰角为25°,测得大树底部C的俯角为45°.已知点A距地面的高度AD为12m,求大树的高度BC.(最后结果精确到0.1)
 21. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
21. AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
①求证:DC为⊙O切线;
②若AD•OC=8,求⊙O半径r.
22.如图所示,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.

(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?
 23. 如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题.
23. 如图,一组正多边形,观察每个正多边形中a的变化情况,解答下列问题. (1)、将表格补充完整.
(1)、将表格补充完整.正多边形的边数
3
4
5
6
α的度数
(2)、观察上面表格中α的变化规律,角α与边数n的关系为 .(3)、根据规律,当α=18°时,多边形边数n= .24. 新定义:在平面直角坐标系中,若几何图形与有公共点,则称几何图形为的关联图形,特别地,若的关联图形为直线,则称该直线为的关联直线.如图,为的关联图形,直线为的关联直线.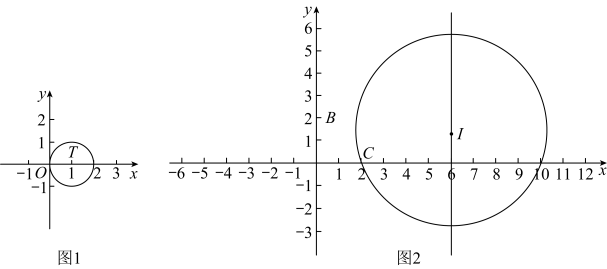
 (1)、已知是以原点为圆心,为半径的圆,下列图形:
(1)、已知是以原点为圆心,为半径的圆,下列图形:直线;直线;双曲线 , 是的关联图形的是(请直接写出正确的序号).
(2)、如图1,的圆心为 , 半径为 , 直线:与轴交于点 , 若直线是的关联直线,求点的横坐标的取值范围.(3)、如图2,已知点 , , , 经过点 , 的关联直线经过点 , 与的一个交点为;的关联直线经过点 , 与的一个交点为;直线 , 交于点 , 若线段在直线上且恰为的直径,请直接写出点横坐标的取值范围.