人教版初中数学几何辅助线进阶训练——构造中线(不含相似)
试卷更新日期:2023-04-27 类型:复习试卷
一、阶段一
-
1. 已知:如图,在 中,是边上的高线,是边上 的中线,G是的中点,连结 , , , .
 (1)、求的长.(2)、求证:.2. 如图,中 , , , , 线段的两个端点、分别在边 , 上滑动,且 , 若点、分别是、的中点,则的最小值为 .
(1)、求的长.(2)、求证:.2. 如图,中 , , , , 线段的两个端点、分别在边 , 上滑动,且 , 若点、分别是、的中点,则的最小值为 . 3.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
3.(1)、【问题情境】课外兴趣小组活动时,老师提出了如下问题:如图1,在△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE,容易证得△ADC≌△EDB,再由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
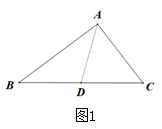 (2)、【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.
(2)、【初步运用】如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长. (3)、【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF.
(3)、【拓展提升】如图3,在△ABC中,D为BC的中点,DE⊥DF分别交AB,AC于点E,F.求证:BE+CF>EF. 4. 如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且 , 则EG的长是 .
4. 如图,在线段AB上取一点C,分别以AC,BC为边长作菱形BCFG和菱形ACDE,使点D在边CF上,连接EG,H是EG的中点,且 , 则EG的长是 . 5. 在中,已知点D、E、F分别是边AE、BF、CD上的中点,若的面积是14,则的面积为 .
5. 在中,已知点D、E、F分别是边AE、BF、CD上的中点,若的面积是14,则的面积为 .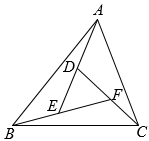 6. 如图, , , , 过C作 , 连接AF与BC相交于点G,若 , 求的度数.
6. 如图, , , , 过C作 , 连接AF与BC相交于点G,若 , 求的度数.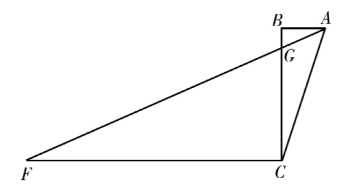 7. 如图,中, , AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24, , 则PE的长是( )
7. 如图,中, , AD平分与BC相交于点D,点E是AB的中点,点F是DC的中点,连接EF交AD于点P.若的面积是24, , 则PE的长是( ) A、2.5 B、2 C、3.5 D、38. 如图所示,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
A、2.5 B、2 C、3.5 D、38. 如图所示,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( ) A、 B、 C、 D、9. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )
A、 B、 C、 D、9. 如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54°,则∠B=( )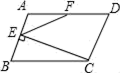 A、54° B、60° C、66° D、72°10.(1)、方法学习:数学兴趣小组活动时,张老师提出了如下问题:如图1,在△ABC中,AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法(如图2),
A、54° B、60° C、66° D、72°10.(1)、方法学习:数学兴趣小组活动时,张老师提出了如下问题:如图1,在△ABC中,AB=8,AC=6,求BC边上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法(如图2),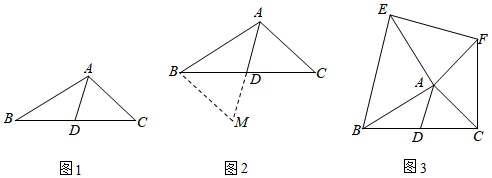
①延长AD到M,使得DM=AD;
②连接BM,通过三角形全等把AB、AC、2AD转化在△ABM中;
③利用三角形的三边关系可得AM的取值范围为AB﹣BM<AM<AB+BM,从而得到AD的取值范围是多少;
(2)、请你写出图2中AC与BM的数量关系和位置关系,并加以证明.(3)、深入思考:如图3,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠CAF=90°,请直接利用(2)的结论,试判断线段AD与EF的数量关系,并加以证明.二、阶段二
-
11. 如图,在中,.将绕顶点C旋转得到 , 若点O是中点,点P是中点,在旋转过程中,线段的最大值等于( )
 A、4 B、6 C、8 D、1012. 如图1,在中,分别是边上的高线,M,N分别是线段的中点.
A、4 B、6 C、8 D、1012. 如图1,在中,分别是边上的高线,M,N分别是线段的中点. (1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.13. 如图,在中,为边的中线,E为上一点,连接并延长交于点F,若 , , , 则的长为.
(1)、求证:.(2)、连接 , 猜想与之间的关系,并说明理由.(3)、若将锐角三角形变为钝角三角形 , 其余条件不变,如图2,直接写出与之间的关系.13. 如图,在中,为边的中线,E为上一点,连接并延长交于点F,若 , , , 则的长为. 14. 如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( )
14. 如图,的面积为12,点D,E,F分别为的中点,则阴影部分的面积为( ) A、2 B、3 C、4 D、615. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
A、2 B、3 C、4 D、615. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )①BF=CF;②若BE⊥AC,则CF=DF;③若BE平分∠ABC,则FG=;④连结EF,若BE⊥AC,则∠DFE=2∠ABE.
 A、①②③ B、③④ C、①②④ D、①②③④16. 阅读理解:亲爱的同学们,在以后的学习中我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半.即:如图1:在中, , 若点是斜边的中点,则 .
A、①②③ B、③④ C、①②④ D、①②③④16. 阅读理解:亲爱的同学们,在以后的学习中我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半.即:如图1:在中, , 若点是斜边的中点,则 . (1)、牛刀小试:在图1中,若 , , 其他条件不变,则;(2)、活学活用:如图2,已知 , 点、分别为、的中点, , . 求的长;(3)、问题解决:为了提高全民健身环境,公园管理部门想要建一个形状如图3中的四边形 , 其中, , , 千米,要在公园的、之间铺设一条笔直的塑胶跑道,若跑道铺设成本每米200元,当最大时,请问管理部门预算160万元够用吗?17. 如图,在中,于点D,于点E,AD与CE相交于点F,连接DE.
(1)、牛刀小试:在图1中,若 , , 其他条件不变,则;(2)、活学活用:如图2,已知 , 点、分别为、的中点, , . 求的长;(3)、问题解决:为了提高全民健身环境,公园管理部门想要建一个形状如图3中的四边形 , 其中, , , 千米,要在公园的、之间铺设一条笔直的塑胶跑道,若跑道铺设成本每米200元,当最大时,请问管理部门预算160万元够用吗?17. 如图,在中,于点D,于点E,AD与CE相交于点F,连接DE. (1)、若 , , , 求 .(2)、若 , , 求 .18. 如图,菱形ABCD的边长是4,∠A=60°,点G为AB的中点,以BG为边作菱形BEFG,其中点E在CB的延长线上,点P为FD的中点,连接PB.则PB= .
(1)、若 , , , 求 .(2)、若 , , 求 .18. 如图,菱形ABCD的边长是4,∠A=60°,点G为AB的中点,以BG为边作菱形BEFG,其中点E在CB的延长线上,点P为FD的中点,连接PB.则PB= . 19. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,BC的中点,连接EF.按以下步骤作图:①分别以点O,C为圆心,大于OC的长为半径作弧,两弧交于点P;②作直线PF,交AC于点G.若AD=4 , BD=8,则线段EF的长为 .
19. 如图,在菱形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,BC的中点,连接EF.按以下步骤作图:①分别以点O,C为圆心,大于OC的长为半径作弧,两弧交于点P;②作直线PF,交AC于点G.若AD=4 , BD=8,则线段EF的长为 .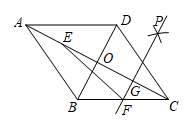 20. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( )
20. 如图,在平行四边形 中, , 于点 , 为 的中点,连结 , ,下列结论:① ,② ;③ ;④ ,其中正确结论的个数共有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个三、阶段三
-
21. 在平行四边形中, , 为中点,点在线段上,连接 , 在下方有一点 , 满足 , 连接 .
 (1)、若 , , 求的面积;(2)、若 , , 求证: .22.
(1)、若 , , 求的面积;(2)、若 , , 求证: .22.
(1)、【探究发现】(1)如图1,中, , , 点为的中点,、分别为边、上两点,若满足 , 则、、之间满足的数量关系是.(2)、【类比应用】如图2,中, , , 点为的中点,、分别为边、上两点,若满足 , 试探究、、之间满足的数量关系,并说明理由.(3)、【拓展延伸】在中, , , 点为的中点,、分别为直线、上两点,若满足 , , 请直接写出的长.23. 如图,在中, , AB=AC=5,点在上,且 , 点E是AB上的动点,连结 , 点 , G分别是BC,DE的中点,连接 , , 当AG=FG时,线段长为 24. 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为 .
24. 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为 . 25. 在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为.
25. 在菱形ABCD中,∠D=60°,CD=4,E为菱形内部一点,且AE=2,连接CE,点F为CE中点,连接BF,取BF中点G,连接AG,则AG的最大值为. 26. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=4.5,S菱形ABCD=36,则OH的长为( )
26. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=4.5,S菱形ABCD=36,则OH的长为( ) A、3 B、3.5 C、4 D、4.527. 点P是平行四边形的对角线所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线作垂线,垂足分别为点E、F.点O为的中点.
A、3 B、3.5 C、4 D、4.527. 点P是平行四边形的对角线所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线作垂线,垂足分别为点E、F.点O为的中点.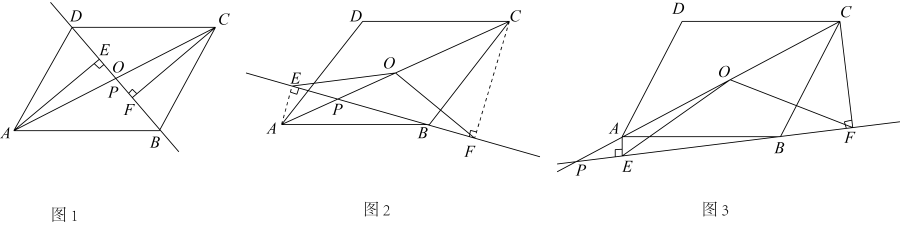 (1)、如图1,当点P与点O重合时,线段和的关系是;(2)、当点P运动到如图2所示的位置时,请证明(1)中的结论仍然成立.(3)、如图3,点P在线段的延长线上运动,当时,试探究线段、、之间的关系.28. 综合与实践
(1)、如图1,当点P与点O重合时,线段和的关系是;(2)、当点P运动到如图2所示的位置时,请证明(1)中的结论仍然成立.(3)、如图3,点P在线段的延长线上运动,当时,试探究线段、、之间的关系.28. 综合与实践问题背景:数学小组在一次课外学习交流时,组内一同学提出如下问题:在 中, ,D为 边上一点,但不与点B,点C重合,过点D作 于点E.连接 ,M为 的中点,连接 , .
(1)、观察发现:如图1, 与 之间的数量关系是; (2)、思考分享:如图2,将 绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长 至点 ,使得 ,连接 运用三角形中位线定理,….按照他的思路或采用其他方法证明;
(2)、思考分享:如图2,将 绕点B顺时针旋转,其他条件不变,则(1)中的结论还成立,请证明.小明是这样思考的:延长 至点 ,使得 ,连接 运用三角形中位线定理,….按照他的思路或采用其他方法证明; (3)、探究计算:若 , , ,在 绕点B旋转一周的过程中,当直线 经过点A时,线段 的长为 .29. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).
(3)、探究计算:若 , , ,在 绕点B旋转一周的过程中,当直线 经过点A时,线段 的长为 .29. 已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为D、E,M为斜边AB的中点(备注,可以直接用结论:直角三角形斜边上的中线等于斜边的一半).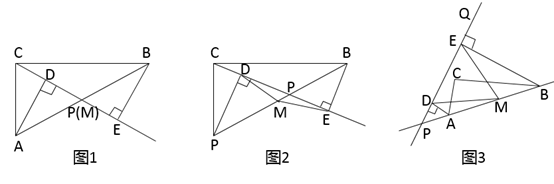 (1)、如图1,当点P与点M重合时,AD与BE的位置关系是 , MD与ME的数量关系是.(2)、如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;(3)、如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.30. 在 与 中, , , ,连接 ,点 为 的中点,连接 , 绕着点 旋转.
(1)、如图1,当点P与点M重合时,AD与BE的位置关系是 , MD与ME的数量关系是.(2)、如图2,当点P在线段AB上不与点M重合时,试判断MD与ME的数量关系,并说明理由;(3)、如图3,当点P在线段BA的延长线上且PQ是不与AB重合的任一直线时,分别过A、B向直线PQ作垂线,垂足分别为D、E,此时(2)中的结论是否成立?若成立,请说明理由.30. 在 与 中, , , ,连接 ,点 为 的中点,连接 , 绕着点 旋转.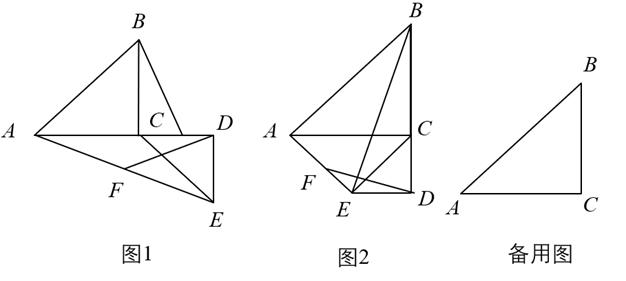 (1)、如图1,当点 落在 的延长线上时, 与 的数量关系是:;(2)、如图2,当 旋转到点 落在 的延长线上时, 与 是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;(3)、旋转过程中,若当 时,直接写出 的值.
(1)、如图1,当点 落在 的延长线上时, 与 的数量关系是:;(2)、如图2,当 旋转到点 落在 的延长线上时, 与 是否仍有具有(1)中的数量关系,如果具有,请给予证明;如果没有,请说明理由;(3)、旋转过程中,若当 时,直接写出 的值.