人教版初中数学几何辅助线进阶训练——构造中位线(适用于八年级)
试卷更新日期:2023-04-27 类型:复习试卷
一、阶段一
-
1. 如图,已知D、E分别是的边、的中点,是的中线,连接、、 , 若的面积为40,则阴影部分的面积为( )
 A、10 B、5 C、8 D、42. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )
A、10 B、5 C、8 D、42. 如图,在中, , , 是边的中点,是边上一点,若平分的周长,则的长为( )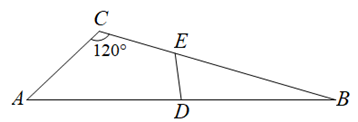 A、 B、 C、 D、3. 如图,在△ABC中,延长BC至点D,使得CD= BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=BC,连接DF,若AB=4,则DF的长为( )
A、 B、 C、 D、3. 如图,在△ABC中,延长BC至点D,使得CD= BC,过AC的中点E作EF∥CD(点F位于点E右侧),且EF=BC,连接DF,若AB=4,则DF的长为( )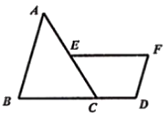 A、3 B、2 C、2 D、4. 如图,在四边形ABCD中,AB⊥BC , AD⊥AC , AD=AC , ∠BAD=105°,点E和点F分别是AC和CD的中点,连接BE , EF , BF , 若CD=8,则 BEF的面积是 .
A、3 B、2 C、2 D、4. 如图,在四边形ABCD中,AB⊥BC , AD⊥AC , AD=AC , ∠BAD=105°,点E和点F分别是AC和CD的中点,连接BE , EF , BF , 若CD=8,则 BEF的面积是 .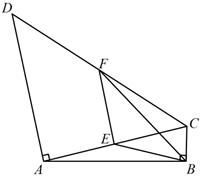 5. 如图,在Rt△ABC中∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,若EF=4,则DE的长为( )
5. 如图,在Rt△ABC中∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,若EF=4,则DE的长为( ) A、4 B、 C、2 D、6. 如图,▱ABCD的顶点C在等边 的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=5,AB=CF=3,则CG的长为 .
A、4 B、 C、2 D、6. 如图,▱ABCD的顶点C在等边 的边BF上,点E在AB的延长线上,G为DE的中点,连接CG.若AD=5,AB=CF=3,则CG的长为 . 7. 如图 ,已知矩形 ABCD ,AD = 12, CD = 9 ,点 R 、P 分别是 DC ,BC 上的定点,点 E 、F 分别是 AP 、 RP 的中点,若CR = 4 ,则 EF =( )
7. 如图 ,已知矩形 ABCD ,AD = 12, CD = 9 ,点 R 、P 分别是 DC ,BC 上的定点,点 E 、F 分别是 AP 、 RP 的中点,若CR = 4 ,则 EF =( ) A、12 B、6.5 C、9 D、不能确定8. 如图,将折叠书架画出侧面示意图,AB面板架,CD为支撑架,EF为锁定杆,F可在CD上移动或固定,已知BC=CE=8cm,如图1,将面板AB竖直固定时(AB⊥BD),点F恰为CD的中点,如图2,当CF=17cm,EF⊥AB,则底部BD=cm,支撑架CD的长度为cm.
A、12 B、6.5 C、9 D、不能确定8. 如图,将折叠书架画出侧面示意图,AB面板架,CD为支撑架,EF为锁定杆,F可在CD上移动或固定,已知BC=CE=8cm,如图1,将面板AB竖直固定时(AB⊥BD),点F恰为CD的中点,如图2,当CF=17cm,EF⊥AB,则底部BD=cm,支撑架CD的长度为cm.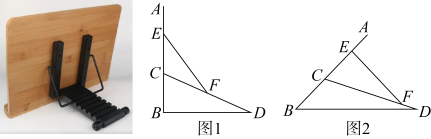 9. 已知是边长为10的等边三角形,为的中点, , 交线段于 , 交的延长线于.若 , 则的长为( )
9. 已知是边长为10的等边三角形,为的中点, , 交线段于 , 交的延长线于.若 , 则的长为( ) A、1 B、2 C、3 D、410. 如图, ABC的中线BE,CD相交于点O,F、G分别是BO、CO的中点,连结DF,EG,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.
A、1 B、2 C、3 D、410. 如图, ABC的中线BE,CD相交于点O,F、G分别是BO、CO的中点,连结DF,EG,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.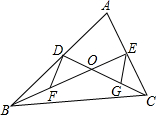
二、阶段二
-
11. 如图,在平行四边形中,对角线 , 相交于点O,在的延长线上取点E,使 , 连接交于点F,若 , 则 .
 12. 如图,在中,是中线,是角平分线,交延长线于点F, , 则的长为 .
12. 如图,在中,是中线,是角平分线,交延长线于点F, , 则的长为 . 13. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=.
13. 如图在平行四边形ABCD中,E是CD的中点,F是AE的中点,CF交BE于点G,若BE=8,则GE=. 14. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 .
14. 如图,在四边形ABCD中,∠A=90°,AB=12,AD=5.点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的最大值是 . 15. 如图,四边形ABCD中.AC⊥BC,// , BD为∠ABC的平分线,BC=6,AC=8.E、F分别是BD、AC的中点,则EF的长为( )
15. 如图,四边形ABCD中.AC⊥BC,// , BD为∠ABC的平分线,BC=6,AC=8.E、F分别是BD、AC的中点,则EF的长为( )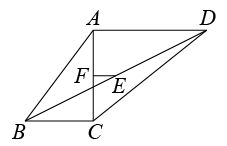 A、2 B、3 C、4 D、516. 如图,已知∠AED=∠ACB=90°,AC=BC=3,AE=DE=1,点D在AB上,连接CE,点M,点N分别为BD,CE的中点,则MN的长为 .
A、2 B、3 C、4 D、516. 如图,已知∠AED=∠ACB=90°,AC=BC=3,AE=DE=1,点D在AB上,连接CE,点M,点N分别为BD,CE的中点,则MN的长为 . 17. 如图, , 、相交于P,E、F分别为、的中点,若 , 则的长是( )
17. 如图, , 、相交于P,E、F分别为、的中点,若 , 则的长是( ) A、1 B、2 C、3 D、418. 如图,△ABC是锐角三角形,分别以AB,AC为边向外侧作等腰△ABM和等腰△CAN,AM=AB AC=AN,∠MAB=∠CAN.D,E,F分别是MB,BC,CN的中点,连结DE,EF.求证:DE=EF。
A、1 B、2 C、3 D、418. 如图,△ABC是锐角三角形,分别以AB,AC为边向外侧作等腰△ABM和等腰△CAN,AM=AB AC=AN,∠MAB=∠CAN.D,E,F分别是MB,BC,CN的中点,连结DE,EF.求证:DE=EF。 19. 如图,在Rt△ABC中,∠B=90°,AB=2 , BC=3,D,E分别是AB,AC的中点,延长BC至点F,使CF=BC,连结DF,EF,则EF的长为。
19. 如图,在Rt△ABC中,∠B=90°,AB=2 , BC=3,D,E分别是AB,AC的中点,延长BC至点F,使CF=BC,连结DF,EF,则EF的长为。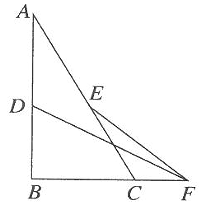 20. 如图,在中,分别是边上的中线,于点O,点F是的中点,若 , 则的长是( )
20. 如图,在中,分别是边上的中线,于点O,点F是的中点,若 , 则的长是( )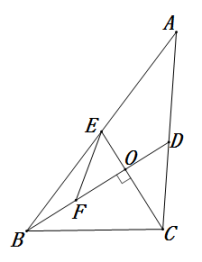 A、7 B、5 C、4 D、3
A、7 B、5 C、4 D、3三、阶段三
-
21. 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB的中点.E,F分别是直线AC,BC上的动点,∠EDF=90°,则线段EF的最小值为 .
 22. 如图,在中, , , 点D、E分别在边AB、AC上, , , 取DE、BC的中点M、N,线段MN的长为( )
22. 如图,在中, , , 点D、E分别在边AB、AC上, , , 取DE、BC的中点M、N,线段MN的长为( )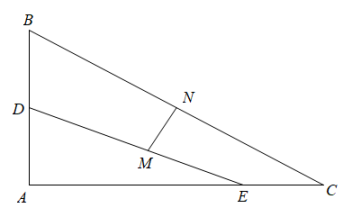 A、2.5 B、3 C、4 D、523. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 .
A、2.5 B、3 C、4 D、523. 如图,在▱ ABCD中,点E、F分别为AD、DC的中点,BF⊥CD,已知BF=8,EF=5,则▱ ABCD的周长为 . 24. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( )
24. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( ) A、 B、 C、 D、25. 如图,在四边形 中, , °, , ,点 分别为 上的动点(含端点), 分别为 的中点,则 长度的最小值为 .
A、 B、 C、 D、25. 如图,在四边形 中, , °, , ,点 分别为 上的动点(含端点), 分别为 的中点,则 长度的最小值为 . 26. 在 中, , , 为 形内一点,以 为腰作等腰 ,使 ,连接 、 ,若 、 分别是 、 的中点, ,则 的长为.
26. 在 中, , , 为 形内一点,以 为腰作等腰 ,使 ,连接 、 ,若 、 分别是 、 的中点, ,则 的长为. 27. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )
27. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )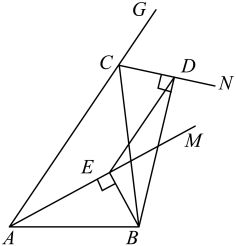 A、 B、 C、 D、28. 如图,在矩形ABCD中, , , 对角线AC,BD相交于点O,点E,F分别为CD,DA延长线上的点,且 , , 连接EF,G为EF的中点,连接OE,交AD于点H,连接GH.
A、 B、 C、 D、28. 如图,在矩形ABCD中, , , 对角线AC,BD相交于点O,点E,F分别为CD,DA延长线上的点,且 , , 连接EF,G为EF的中点,连接OE,交AD于点H,连接GH. (1)、求证:H是OE的中点;(2)、求GH的长.29. 如图,矩形ABCD中,AB=2,AD=4,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是.
(1)、求证:H是OE的中点;(2)、求GH的长.29. 如图,矩形ABCD中,AB=2,AD=4,E为BC的中点,F为DE上一动点,P为AF中点,连接PC,则PC的最小值是. 30. 如图1,点是线段上一点 , 分别以、为直角边,在同侧作等腰直角三角形和 , 点、分别是斜边、的中点,点是线段的中点,连接、.
30. 如图1,点是线段上一点 , 分别以、为直角边,在同侧作等腰直角三角形和 , 点、分别是斜边、的中点,点是线段的中点,连接、. (1)、观察猜想,图1中,线段与的数量关系是 , 位置关系是;(2)、探究证明:将图1中的绕着点顺时针旋转 , 如图2,点、、依然分别是、、的中点,请判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.(3)、若将图1中和都换成等边三角形,将图1中的绕着点顺时针旋转 , 如图3,点、、P依然分别是、、的中点,请判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
(1)、观察猜想,图1中,线段与的数量关系是 , 位置关系是;(2)、探究证明:将图1中的绕着点顺时针旋转 , 如图2,点、、依然分别是、、的中点,请判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.(3)、若将图1中和都换成等边三角形,将图1中的绕着点顺时针旋转 , 如图3,点、、P依然分别是、、的中点,请判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.