四川省德阳市旌阳区2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 若一个数的倒数恰好等于这个数本身,则这个数是( )A、1 B、-1 C、1,-1 D、1,0,-12. 我国是世界人口大国,中央高度重视粮食安全,要求坚决守住1 800 000 000亩耕地红线.将数据1 800 000 000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 下列说法中,正确的是( )A、为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 B、旅客上飞机前的安检,采用抽样调查方式 C、某同学连续5次抛掷质量均匀的硬币,1次正面向上,因此正面向上的概率是20% D、在连续6次数学测试中,两名同学的平均分相同,方差较小的同学数学成绩更稳定5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,∠ACD是 ABC的一个外角,CE平分∠ACD,F为CA延长线上的一点,FG CE,交AB于点G,若∠1=70°,∠2=36°,则∠3=( )
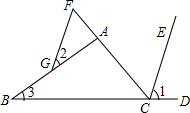 A、36° B、40° C、34° D、70°7. 智能垃圾箱分为“有害垃圾、可回收垃圾”等若干箱体.居民通过刷卡、手机号、人脸识别等身份识别方式进行自动开箱投放,将不同的垃圾投放至不同的箱体内,垃圾箱则根据居民投放的垃圾,自动进行称重,然后换算出积分可以现金提现或在礼品兑换机兑换实物礼品.我市某小区7个家庭一周换算的积分分别为23,25,25,23,30,27,25.关于这组数据,中位数和众数分别是( )A、23,25 B、25,23 C、23,23 D、25,258. 某圆锥的三视图如图所示,由图中数据可知,该圆锥的侧面积为( )
A、36° B、40° C、34° D、70°7. 智能垃圾箱分为“有害垃圾、可回收垃圾”等若干箱体.居民通过刷卡、手机号、人脸识别等身份识别方式进行自动开箱投放,将不同的垃圾投放至不同的箱体内,垃圾箱则根据居民投放的垃圾,自动进行称重,然后换算出积分可以现金提现或在礼品兑换机兑换实物礼品.我市某小区7个家庭一周换算的积分分别为23,25,25,23,30,27,25.关于这组数据,中位数和众数分别是( )A、23,25 B、25,23 C、23,23 D、25,258. 某圆锥的三视图如图所示,由图中数据可知,该圆锥的侧面积为( ) A、 B、 C、 D、9. 如图,是正方形边上一点,将绕点顺时针旋转得 , 连接 , 过点作的垂线交于点 , 交于点.若 , , 则的长为( )
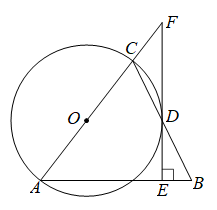
A、 B、 C、 D、9. 如图,是正方形边上一点,将绕点顺时针旋转得 , 连接 , 过点作的垂线交于点 , 交于点.若 , , 则的长为( ) A、 B、 C、4 D、10. 若实数m使关于x的不等式组有解且至多有3个整数解,且使关于y的分式方程的解为非负数解,则满足条件的所有整数m的和为( )A、6 B、10 C、11 D、1511. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )
A、 B、 C、4 D、10. 若实数m使关于x的不等式组有解且至多有3个整数解,且使关于y的分式方程的解为非负数解,则满足条件的所有整数m的和为( )A、6 B、10 C、11 D、1511. 如图,半径为 , 正方形内接于 , 点E在上运动,连接作 , 垂足为F,连接.则长的最小值为( )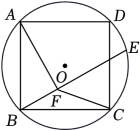 A、 B、1 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )
A、 B、1 C、 D、12. 如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(5,0),与y轴交于点C,其对称轴为直线x=2,结合图象分析如下结论:①abc>0;②b+3a<0;③当x>0时,y随x的增大而增大;④若一次函数y=kx+b(k≠0)的图象经过点A,则点E(k,b)在第四象限;⑤点M是抛物线的顶点,若CM⊥AM,则a= . 其中正确的有( )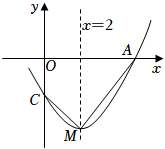 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 分解因式: .14. 若数据2,1,a,3,0的平均数是2,则这组数据的方差是.15. 材料:从 三人中选取二人当代表,有 和 和 和 三种不同的选法,抽象成数学模型是:从3个元素中选取2个元素组合,记作 .一般地,从 个元素中选取 个元素组合,记作 .
问题:从7个人中选取4个人当代表,不同的选法有种.
16. 如图有两张正方形纸片A和B,图1将B放置在A内部,测得阴影部分面积为3;图2将正方形AB并列放置后构造新正方形,测得阴影部分面积为21;若将3个正方形A和2个正方形B并列放置后构造新正方形如图3 (图2,图3中正方形AB纸片均无重叠部分),则图3阴影部分面积是 17. 如图,为等边三角形,点的坐标为 , 过点作直线交于 , 交于 , 点在反比例函数的图像上,当和的面积相等时,的值是.
17. 如图,为等边三角形,点的坐标为 , 过点作直线交于 , 交于 , 点在反比例函数的图像上,当和的面积相等时,的值是. 18. 如图,中,; 和都是等边三角形,为的中点,连接交于点 , 与交于点;以下结论:①;②四边形为菱形;③;④.其中,正确的结论有.(填写所有正确结论的序号)
18. 如图,中,; 和都是等边三角形,为的中点,连接交于点 , 与交于点;以下结论:①;②四边形为菱形;③;④.其中,正确的结论有.(填写所有正确结论的序号)
三、解答题
-
19. 计算:.20. 某校组织全校学生进行了“航天知识竞赛”,教务处从中随机抽取了n名学生的竞赛成绩(满分100分,每名学生的成绩记为x分)分成如表中四组,并得到如下不完整的频数分布表、频数分布直方图和扇形统计图.根据图中信息,解答下列问题:
分组
频数
A:
a
B:
18
C:
24
D:
b
 (1)、n的值为 , a的值为 , b的值为;(2)、请补全频数分布直方图并计算扇形统计图中表示“C”的圆心角的度数为 ▲ °;(3)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机为抽取两名宣讲航天知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.21. 如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,
(1)、n的值为 , a的值为 , b的值为;(2)、请补全频数分布直方图并计算扇形统计图中表示“C”的圆心角的度数为 ▲ °;(3)、竞赛结束后,九年级一班从本班获得优秀的甲、乙、丙、丁四名同学中随机为抽取两名宣讲航天知识,请用列表或画树状图的方法求恰好抽到甲、乙两名同学的概率.21. 如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使得CF=BE,连接DF,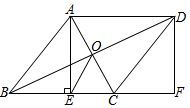 (1)、求证:四边形AEFD是矩形;(2)、连接OE,若AB=13,OE=2 , 求AE的长.22. 已知直线与反比例函数的图象在第一象限交于点.
(1)、求证:四边形AEFD是矩形;(2)、连接OE,若AB=13,OE=2 , 求AE的长.22. 已知直线与反比例函数的图象在第一象限交于点.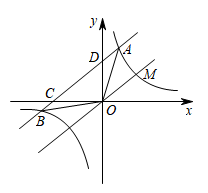 (1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.23. 平安路上,多“盔”有你,在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价2元,平均每周可多售出40顶.(1)、若该商店希望平均每周获利4000元,则每顶头盔应降价多少?(2)、商店降价销售后,决定每销售1顶头盔就向某慈善机构捐赠m元(m为整数,且),帮助做“交通安全”宣传.捐赠后发现,该商店每周销售这种商品的利润仍随售价的增大而增大,求m的值.
(1)、求反比例函数的解析式;(2)、如图,将直线向上平移个单位后与的图象交于点和点 , 求的值;(3)、在(2)的条件下,设直线与轴、轴分别交于点 , , 求证:.23. 平安路上,多“盔”有你,在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价2元,平均每周可多售出40顶.(1)、若该商店希望平均每周获利4000元,则每顶头盔应降价多少?(2)、商店降价销售后,决定每销售1顶头盔就向某慈善机构捐赠m元(m为整数,且),帮助做“交通安全”宣传.捐赠后发现,该商店每周销售这种商品的利润仍随售价的增大而增大,求m的值.