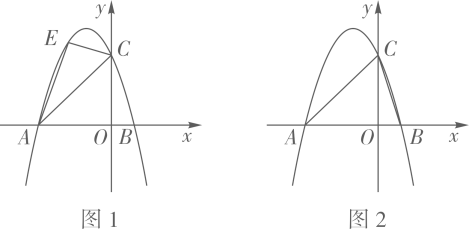四川省达州市开江县2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
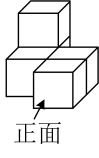
1. 下列实数中,比﹣2小的数是( )A、﹣1 B、5 C、﹣5 D、12. 下列各式计算正确的是( )A、 B、 C、 D、3. 如图是由5个相同的小正方体组成的立体图形,它的左视图是( )
 A、
A、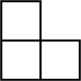 B、
B、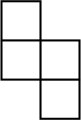 C、
C、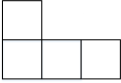 D、
D、 4. 如图,生活中,将一个宽度相等的纸条按图所示折叠一下,如果 , 那么的度数为( )
4. 如图,生活中,将一个宽度相等的纸条按图所示折叠一下,如果 , 那么的度数为( )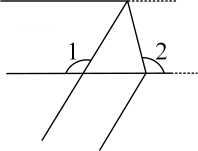 A、 B、 C、 D、5. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、6. 年国内生产总值增长5.5%左右,城镇新增就业1200万人以上,请将数“1200万”用科学记数法表示为( )A、 B、 C、 D、7.
A、 B、 C、 D、5. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、6. 年国内生产总值增长5.5%左右,城镇新增就业1200万人以上,请将数“1200万”用科学记数法表示为( )A、 B、 C、 D、7.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为( )
 A、2 B、4 C、4 D、88. 如图,在平行四边形ABCD中, , , , 过的中点作 , 垂足为点 , 延长交的延长线于点 , 连接 , 则的长为( )
A、2 B、4 C、4 D、88. 如图,在平行四边形ABCD中, , , , 过的中点作 , 垂足为点 , 延长交的延长线于点 , 连接 , 则的长为( )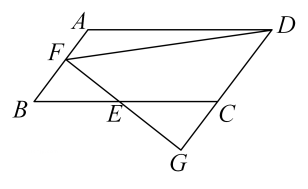 A、4 B、 C、8 D、9. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )
A、4 B、 C、8 D、9. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …,An在x轴上,点B1 , B2 , …,B在直线上,若点A1的坐标为(1,0),且 , , …,都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1 , S2 , …,Sn , 则Sn可表示为( )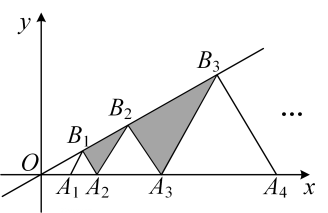 A、 B、 C、 D、10. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( )
A、 B、 C、 D、10. 求二次函数 的图象如图所示,其对称轴为直线 ,与 轴的交点为 、 ,其中 ,有下列结论:① ;② ;③ ;④ ;⑤ ;其中,正确的结论有( ) A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、填空题
-
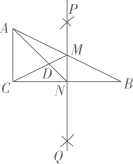
11. 因式分解: .12. 已知、是一元二次方程的两个实数根,则的值是.13. 如图,在中, , , 分别以点 , 为圆心,大于的长为半径作弧,两弧交于点、 , 作直线交、于点、 , 连接、 , 则.
 14. 如图,正方形的边长为4,A、两点分别位于轴、轴上,点在上,交于点 , 函数的图象经过点 , 若 , 则的值为.
14. 如图,正方形的边长为4,A、两点分别位于轴、轴上,点在上,交于点 , 函数的图象经过点 , 若 , 则的值为.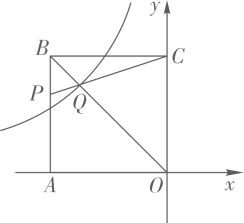
三、解答题
-
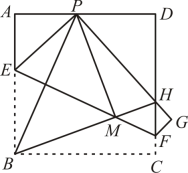
15. 如图,将正方形纸片沿折叠,使点落在边的点处(不与点 , 点重合),点落在点处,交于点 , 连接、 , 交于点 , 连接 , 下列结论:①;②平分;③;④;⑤若 , , 则 , 其中正确结论的序号是.
 16.(1)、计算:;(2)、 , 选一个适合的数代入求值.17. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况进行团史学习,现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用表示),其中记为“较差”,记为“一般”,记为“良好”,记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.
16.(1)、计算:;(2)、 , 选一个适合的数代入求值.17. 今年是中国共产主义青年团成立100周年,某校组织学生观看庆祝大会实况进行团史学习,现随机抽取部分学生进行团史知识竞赛,并将竞赛成绩(满分100分)进行整理(成绩得分用表示),其中记为“较差”,记为“一般”,记为“良好”,记为“优秀”,绘制了不完整的扇形统计图和频数分布直方图.请根据统计图提供的信息,回答如下问题:
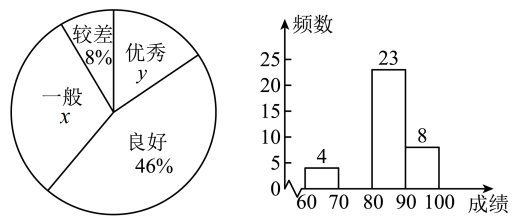 (1)、 ▲ , ▲ , 并将直方图补充完整;(2)、已知这组的具体成绩为93,94,99,91,100,94,96,98,这8个数据的中位数是 , 众数是;(3)、本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.18. 北京冬奥会首钢滑雪大跳台以飘带曲线构筑的建筑外形十分优美、流畅,向世界传递出了中国式的浪漫.某小组开展数学实践活动,在大跳台另一侧进行测量.如图,已知测倾器高度为1米,在测点A处安置测倾器,测得点P处的仰角∠PBE=45°,在与点A相距7.8米的测点C处安置测倾器,测得点P处的仰角∠PDE=50°(A,C与Q在一条直线上),求首钢大跳台起点到地面的高度PQ.(参考数据:tan50°≈1.20,sin50°≈0.77,cos50°≈0.64,计算结果精确到1米)
(1)、 ▲ , ▲ , 并将直方图补充完整;(2)、已知这组的具体成绩为93,94,99,91,100,94,96,98,这8个数据的中位数是 , 众数是;(3)、本次知识竞赛超过95分的学生中有3名女生,1名男生,现从以上4人中随机抽取2人去参加全市的团史知识竞赛,请用列表或画树状图的方法,求恰好抽中2名女生参加知识竞赛的概率.18. 北京冬奥会首钢滑雪大跳台以飘带曲线构筑的建筑外形十分优美、流畅,向世界传递出了中国式的浪漫.某小组开展数学实践活动,在大跳台另一侧进行测量.如图,已知测倾器高度为1米,在测点A处安置测倾器,测得点P处的仰角∠PBE=45°,在与点A相距7.8米的测点C处安置测倾器,测得点P处的仰角∠PDE=50°(A,C与Q在一条直线上),求首钢大跳台起点到地面的高度PQ.(参考数据:tan50°≈1.20,sin50°≈0.77,cos50°≈0.64,计算结果精确到1米) 19. 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
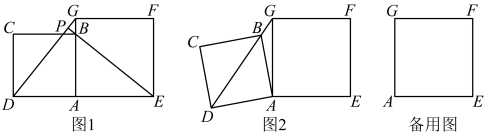
19. 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)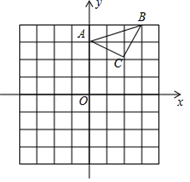 (1)、画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1 , 并直接写出C1点的坐标;(2)、画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 , 并直接写出C2点的坐标;(3)、请求出(2)中△ABC旋转过程中所扫过的面积为 .20. 如图,在四边形中, , 对角线 , 交于点 , , 且平分 , 过点作交的延长线于点.
(1)、画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1 , 并直接写出C1点的坐标;(2)、画出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2 , 并直接写出C2点的坐标;(3)、请求出(2)中△ABC旋转过程中所扫过的面积为 .20. 如图,在四边形中, , 对角线 , 交于点 , , 且平分 , 过点作交的延长线于点.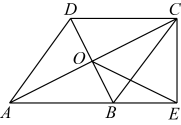 (1)、求证:四边形是菱形;(2)、若 , , 求的面积.21. 某超市经销一种商品,每千克成本为40元,试经销发现,该种商品的每天销售量y(件数)与销售单价x(元/件)满足一次函数关系,其每天销售单价,销售量的几组对应值如下表所示:
(1)、求证:四边形是菱形;(2)、若 , , 求的面积.21. 某超市经销一种商品,每千克成本为40元,试经销发现,该种商品的每天销售量y(件数)与销售单价x(元/件)满足一次函数关系,其每天销售单价,销售量的几组对应值如下表所示:销售单价x(元/件)
55
60
70
…
销售量y(件)
70
60
40
…
(1)、直接写出y(件)与x(元/件)之间的函数表达式;(2)、求销售单价定为多少时,当天的销售利润是1050元?(3)、销售过程中要求走出的商品数不少于60件,求销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?22. 如图,AB是⊙O的直径,点F在⊙O上,∠BAF的平分线AE交⊙O于点E,过点E作ED⊥AF,分别交AB、AF的延长线于点C、D.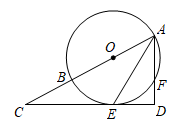 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5, ,求BC的长.23. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”,例如:点是函数的图像的“等值点”.(1)、分别判断函数 , 的图像上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、设函数 , 的图像的“等值点”分别为点 , , 过点作轴,垂足为.当的面积为3时,求的值;(3)、若函数的图像记为 , 将其沿直线翻折后的图像记为 , 当 , 两部分组成的图像上恰有2个“等值点”时,直接写出的取值范围.
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为5, ,求BC的长.23. 定义:若一个函数图象上存在横、纵坐标相等的点,则称该点为这个函数图象的“等值点”,例如:点是函数的图像的“等值点”.(1)、分别判断函数 , 的图像上是否存在“等值点”?如果存在,求出“等值点”的坐标;如果不存在,说明理由;(2)、设函数 , 的图像的“等值点”分别为点 , , 过点作轴,垂足为.当的面积为3时,求的值;(3)、若函数的图像记为 , 将其沿直线翻折后的图像记为 , 当 , 两部分组成的图像上恰有2个“等值点”时,直接写出的取值范围.