江苏省泰州市姜堰区2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、-5 B、-1 C、1 D、52. 下列式子中,计算正确的是( )A、a3+a3=a6 B、(﹣a2)3=﹣a6 C、a2•a3=a6 D、(a+b)2=a2+b23. 下面的几何体中,主(正)视图为三角形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 已知a、b、c为常数,点P(a,c)在第二象限,则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断5. 若不等式组 恰有两个整数解,则 的取值范围是( ).A、 B、 C、 D、6. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )
4. 已知a、b、c为常数,点P(a,c)在第二象限,则关于x的方程ax2+bx+c=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法判断5. 若不等式组 恰有两个整数解,则 的取值范围是( ).A、 B、 C、 D、6. 在平面直角坐标系中,点A在直线l上,以A为圆心,为半径的圆与y轴的另一个交点为E,给出如下定义:若线段 , 和直线l上分别存在点B,点C和点D,使得四边形是矩形(点顺时针排列),则称矩形为直线l的“理想矩形”.例如,右图中的矩形为直线l的“理想矩形”.若点 , 则直线的“理想矩形”的面积为( )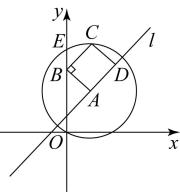 A、12 B、 C、 D、
A、12 B、 C、 D、二、填空题
-
7. 分解因式:.8. 光速是每秒30万公里,每小时1080000000公里,用科学记数法表示1 080 000 000是9. 函数 中自变量x的取值范围是 .10. 新冠肺炎是一种传染性极强的疾病,如果有一人患病,经过两轮传染后有100人患病,设每轮传染中平均一个人传染了x个人,则由题意列出方程.11. 如图,点C在线段 上,且 ,分别以 、 为边在线段 的同侧作正方形 、 ,连接 、 ,则 .
 12. 已知二次函数y=x2-4x+3,当a≤x≤a+5时,函数y的最小值为-1,则a的取值范围是.13. 如图,在△ABC中,∠CAB=40°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为.
12. 已知二次函数y=x2-4x+3,当a≤x≤a+5时,函数y的最小值为-1,则a的取值范围是.13. 如图,在△ABC中,∠CAB=40°,将△ABC在平面内绕点A逆时针旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为.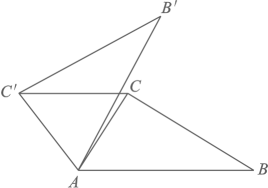 14. 《九章算术》是我国古代数学名著,书中记载:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱,问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为.15. 如图,在△ABC中,AB=AC=5,BC=4 ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为.
14. 《九章算术》是我国古代数学名著,书中记载:“今有人合伙买羊,每人出5钱,还差45钱;每人出7钱,还差3钱,问合伙人数、羊价各是多少?”设合伙人数为x人,根据题意可列一元一次方程为.15. 如图,在△ABC中,AB=AC=5,BC=4 ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为.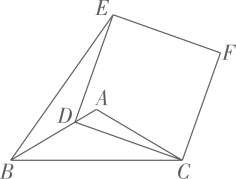 16. 在平面直角坐标系中有一点 , 若a为任意实数,点P的坐标为(a+1,2a+1),则PQ的最小值为.
16. 在平面直角坐标系中有一点 , 若a为任意实数,点P的坐标为(a+1,2a+1),则PQ的最小值为.三、解答题
-
17.(1)、计算:;(2)、18. 先化简,再求值: ,其中 .19. “2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动.规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.(1)、在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;(2)、再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.20. 某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型
频数
频率
书法类
18
a
围棋类
14
0.28
喜剧类
8
0.16
国画类
b
0.20
根据以上信息完成下列问题:
 (1)、直接写出频数分布表中a的值;(2)、补全频数分布条形图;(3)、若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?21. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润各多少元?(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑a台,这100台电脑的销售总利润为w元.
(1)、直接写出频数分布表中a的值;(2)、补全频数分布条形图;(3)、若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?21. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润各多少元?(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑a台,这100台电脑的销售总利润为w元.①求关于a的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
22. 如图,小王在长江边某瞭望台D处测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为多少米?(结果精确到0.1,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)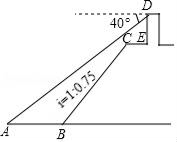 23. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.
23. 如图,在△ABC中,AB=AC,以AB为直径作⊙O,⊙O交BC于点D,交CA的延长线于点E.过点D作DF⊥AC,垂足为F.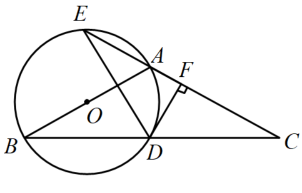 (1)、求证:DF为⊙O的切线;(2)、若AB=4,∠C=30°,求劣弧的长.24. 已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C.
(1)、求证:DF为⊙O的切线;(2)、若AB=4,∠C=30°,求劣弧的长.24. 已知二次函数y=x2+mx+n的图象经过点A(1,0)和D(4,3),与x轴的另一个交点为B,与y轴交于点C. (1)、求二次函数的表达式及顶点坐标;(2)、将二次函数y=x2+mx+n的图象在点B、C之间的部分(包含点B、C)记为图象G.已知直线l:y=kx-2k+2总位于图象G的上方,请直接写出k的取值范围;(3)、如果点P(x1 , c)和点Q(x2 , c)在函数y=x2+mx+n的图象上,且x1<x2 , PQ=2a,求x12-ax2+6a+4的值.25. 已知抛物线y=ax2+3ax+c(a≠0)与y轴交于点A(1)、若a>0
(1)、求二次函数的表达式及顶点坐标;(2)、将二次函数y=x2+mx+n的图象在点B、C之间的部分(包含点B、C)记为图象G.已知直线l:y=kx-2k+2总位于图象G的上方,请直接写出k的取值范围;(3)、如果点P(x1 , c)和点Q(x2 , c)在函数y=x2+mx+n的图象上,且x1<x2 , PQ=2a,求x12-ax2+6a+4的值.25. 已知抛物线y=ax2+3ax+c(a≠0)与y轴交于点A(1)、若a>0①当a=1,c=-1,求该抛物线与x轴交点坐标;
②点P(m,n)在二次函数抛物线y=ax2+3ax+c的图象上,且n-c>0,试求m的取值范围;
(2)、若抛物线恒在x轴下方,且符合条件的整数a只有三个,求实数c的最小值;(3)、若点A的坐标是(0,1),当-2c<x<c时,抛物线与x轴只有一个公共点,求a的取值范围.26. 如图,在中, , , 过点A作 , 垂足为 , 且 , 是线段上一点,过作 , 垂足为F.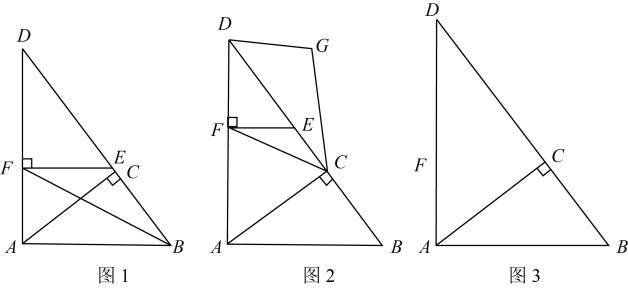 (1)、请直接写出的长为;(2)、如图1,若点在的角平分线上,求的长;(3)、如图2,连接 , 点为点A关于的对称点.
(1)、请直接写出的长为;(2)、如图1,若点在的角平分线上,求的长;(3)、如图2,连接 , 点为点A关于的对称点.①连结 , , 当四边形中有两边互相平行时,求的长;
②连结交于点 , 点在点的上方,若 , 则 ▲ .