江苏省泰州市2023年九年级中考数学一模模拟试卷
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 下列说法正确的是( )A、为了解我国中小学生的睡眠情况,应采取全面调查的方式 B、一组数据1,2,5,5,5,3,3的众数和平均数都是3 C、若甲、乙两组数的方差分别是0.01,0.1,则甲组数据比乙组数据更稳定 D、抛掷一枚硬币200次,一定有100次“正面向上”2. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、63. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
 A、10° B、15° C、20° D、30°4. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、5. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )
A、10° B、15° C、20° D、30°4. 一个扇形的弧长是 , 其圆心角是150°,此扇形的面积为( )A、 B、 C、 D、5. 如图,在四边形ABCD中,∠A=∠B=90°,AD=10cm,BC=8cm,点P从点D出发,以1cm/s的速度向点A运动,点M从点B同时出发,以相同的速度向点C运动,当其中一个动点到达端点时,两个动点同时停止运动.设点P的运动时间为t(单位:s),下列结论正确的是( )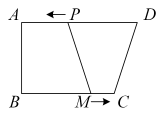 A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s6. 已知抛物线 , 当时,;当时,.下列判断:
A、当时,四边形ABMP为矩形 B、当时,四边形CDPM为平行四边形 C、当时, D、当时,或6s6. 已知抛物线 , 当时,;当时,.下列判断:①;②若 , 则;③已知点 , 在抛物线上,当时,;④若方程的两实数根为 , , 则.
其中正确的有( )个.
A、1 B、2 C、3 D、4二、填空题
-
7. 分解因式: .8. 从2名男生和2名女生中任选2名学生参加志愿者服务,那么选出的2名学生中至少有1名女生的概率是.9. 在反比例的图象的每一支上,y都随x的增大而减小,且整式是一个完全平方式,则该反比例函数的解析式为.10. 如图,扇形 中, , ,点 为 上一点,将扇形 沿 折叠,使点 的对应点 落在射线 上,则图中阴影部分的面积为.
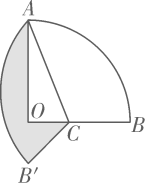 11. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是.
11. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是. 12. 观察下列一组数:2, , , …,它们按一定规律排列,第n个数记为 , 且满足.则 , .13. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是.
12. 观察下列一组数:2, , , …,它们按一定规律排列,第n个数记为 , 且满足.则 , .13. 如图,已知是内的一点, , , 若的面积为2, , , 则的面积是. 14. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为.
14. 如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,与反比例函数的图象在第一象限交于点C,若 , 则k的值为. 15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.
15. 如图,把边长为1:2的矩形ABCD沿长边BC,AD的中点E,F对折,得到四边形ABEF,点G,H分别在BE,EF上,且BG=EH=BE=2,AG与BH交于点O,N为AF的中点,连接ON,作OM⊥ON交AB于点M,连接MN,则tan∠AMN=.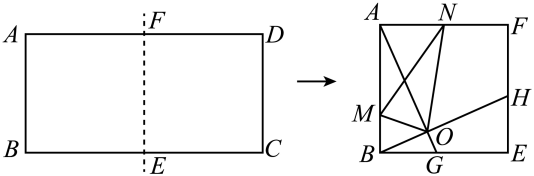 16. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为.
16. 中, , , , E是AC的中点,MN分别是边AB、BC上的动点,D也是BC边上的一个动点,以CD为直径作 , 连接ED交于F,连接FM,MN,则的最小值为.
三、解答题
-
17. 如图,在平面直角坐标系中,△ABC和△A1B1C1关于点E成中心对称.

⑴画出对称中心E,并写出点E、A、C的坐标;
⑵P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P2(a+6,b+2),请画出上述平移后的△A2B2C2 , 并写出点A2、C2的坐标;
⑶判断△A2B2C2和△A1B1C1的位置关系(直接写出结果).
18.(1)、化简:;(2)、解不等式组 , 并把它的解集在数轴上表示出来.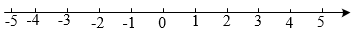 19. 电视剧《一代洪商》在中央电视台第八套播出后,怀化市各旅游景点知名度得到显菩提高.为全面提高旅游服务质量,旅游管理部门随机抽取了100名游客进行满意度调查,并绘制成如下不完整的频数分布表和扇形统计图.
19. 电视剧《一代洪商》在中央电视台第八套播出后,怀化市各旅游景点知名度得到显菩提高.为全面提高旅游服务质量,旅游管理部门随机抽取了100名游客进行满意度调查,并绘制成如下不完整的频数分布表和扇形统计图.频数分布表
满意程度
频数(人)
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1

根据统计图表提供的信息,解答下列问题:
(1)、a= , b= , c=;(2)、求扇形统计图中表示“一般”的扇形圆心角α的度数;(3)、根据调查情况,请你对各景点的服务提一至两条合理建议.20. 如图,△ABC内接于⊙O,P是⊙O的直径AB延长线上一点,∠PCB=∠OAC,过点O作BC的平行线交PC的延长线于点D.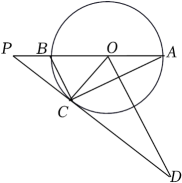 (1)、试判断PC与⊙O的位置关系,并说明理由;(2)、若PC=4,tanA= , 求△OCD的面积.21. 亚洲第一、中国唯一的航空货运枢纽一一鄂州花湖机场,于2022年3月19日完成首次全货运试飞,很多市民共同见证了这一历史时刻.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,若斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).求:
(1)、试判断PC与⊙O的位置关系,并说明理由;(2)、若PC=4,tanA= , 求△OCD的面积.21. 亚洲第一、中国唯一的航空货运枢纽一一鄂州花湖机场,于2022年3月19日完成首次全货运试飞,很多市民共同见证了这一历史时刻.如图,市民甲在C处看见飞机A的仰角为45°,同时另一市民乙在斜坡CF上的D处看见飞机A的仰角为30°,若斜坡CF的坡比=1:3,铅垂高度DG=30米(点E、G、C、B在同一水平线上).求: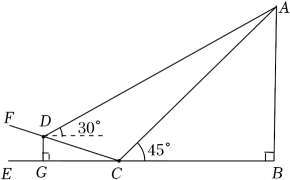 (1)、两位市民甲、乙之间的距离CD;(2)、此时飞机的高度AB,(结果保留根号)22. 如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C.
(1)、两位市民甲、乙之间的距离CD;(2)、此时飞机的高度AB,(结果保留根号)22. 如图,P为⊙O外一点,PA、PB为⊙O的切线,切点分别为A、B,直线PO交⊙O于点D、E,交AB于点C. (1)、求证:∠ADE=∠PAE.(2)、若∠ADE=30°,求证:AE=PE.(3)、若PE=4,CD=6,求CE的长.23. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.
(1)、求证:∠ADE=∠PAE.(2)、若∠ADE=30°,求证:AE=PE.(3)、若PE=4,CD=6,求CE的长.23. 如图, , , 点A,B分别在函数()和()的图象上,且点A的坐标为.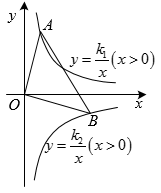 (1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.24. 某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.(1)、求该产品第一年的利润w(万元)与售价x之间的函数关系式;(2)、该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?25. 如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.
(1)、求 , 的值:(2)、若点C,D分在函数()和()的图象上,且不与点A,B重合,是否存在点C,D,使得 , 若存在,请直接出点C,D的坐标:若不存在,请说明理由.24. 某企业投入60万元(只计入第一年成本)生产某种产品,按网上订单生产并销售(生产量等于销售量).经测算,该产品网上每年的销售量y(万件)与售价x(元/件)之间满足函数关系式y=24-x,第一年除60万元外其他成本为8元/件.(1)、求该产品第一年的利润w(万元)与售价x之间的函数关系式;(2)、该产品第一年利润为4万元,第二年将它全部作为技改资金再次投入(只计入第二年成本)后,其他成本下降2元/件.①求该产品第一年的售价;②若第二年售价不高于第一年,销售量不超过13万件,则第二年利润最少是多少万元?25. 如图1,在平面直角坐标系中,Rt△OAB的直角边OA在y轴的正半轴上,且OA=6,斜边OB=10,点P为线段AB上一动点.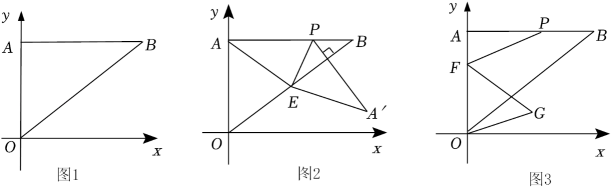 (1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.26. 如图一所示,在平面直角坐标中,抛物线y=ax2+2x+c经过点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为点D.在线段CB上方的抛物线上有一动点P,过点P作PE⊥BC于点E,作PFAB交BC于点F.
(1)、请直接写出点B的坐标;(2)、若动点P满足∠POB=45°,求此时点P的坐标;(3)、如图2,若点E为线段OB的中点,连接PE,以PE为折痕,在平面内将△APE折叠,点A的对应点为A',当PA'⊥OB时,求此时点P的坐标;(4)、如图3,若F为线段AO上一点,且AF=2,连接FP,将线段FP绕点F顺时针方向旋转60°得线段FG,连接OG,当OG取最小值时,请直接写出OG的最小值和此时线段FP扫过的面积.26. 如图一所示,在平面直角坐标中,抛物线y=ax2+2x+c经过点A(﹣1,0)、B(3,0),与y轴交于点C,顶点为点D.在线段CB上方的抛物线上有一动点P,过点P作PE⊥BC于点E,作PFAB交BC于点F.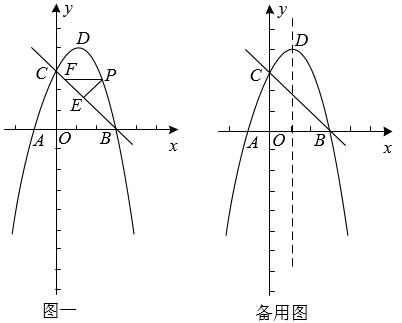 (1)、求抛物线和直线BC的函数表达式,(2)、当△PEF的周长为最大值时,求点P的坐标和△PEF的周长.(3)、若点G是抛物线上的一个动点,点M是抛物线对称轴上的一个动点,是否存在以C、B、G、M为顶点的四边形为平行四边形?若存在,求出点G的坐标,若不存在,请说明理由.
(1)、求抛物线和直线BC的函数表达式,(2)、当△PEF的周长为最大值时,求点P的坐标和△PEF的周长.(3)、若点G是抛物线上的一个动点,点M是抛物线对称轴上的一个动点,是否存在以C、B、G、M为顶点的四边形为平行四边形?若存在,求出点G的坐标,若不存在,请说明理由.