江苏省淮安市淮阴区2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 2的倒数是( )。A、2 B、 C、 D、-22. 下列图标,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 3. 人体最小的细胞是血小板.5000000个血小板紧密排成一直线长约 , 数据5000000用科学记数法表示是( )A、 B、 C、 D、4. 同时抛掷两枚质地均匀的正方体骰子1次,下列事件中是不可能事件的是( )A、朝上的点数之和为12 B、朝上的点数之和为13 C、朝上的点数之和为2 D、朝上的点数之和小于95. 已知的半径为5,直线与有2个公共点,则点到直线的距离可能是( )A、3 B、5 C、7 D、96. 在平面直角坐标系中,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若干桶方便面摆放在桌面上,它的三个视图如下,则这一堆方便面共有( )
3. 人体最小的细胞是血小板.5000000个血小板紧密排成一直线长约 , 数据5000000用科学记数法表示是( )A、 B、 C、 D、4. 同时抛掷两枚质地均匀的正方体骰子1次,下列事件中是不可能事件的是( )A、朝上的点数之和为12 B、朝上的点数之和为13 C、朝上的点数之和为2 D、朝上的点数之和小于95. 已知的半径为5,直线与有2个公共点,则点到直线的距离可能是( )A、3 B、5 C、7 D、96. 在平面直角坐标系中,点一定在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若干桶方便面摆放在桌面上,它的三个视图如下,则这一堆方便面共有( ) A、7桶 B、8桶 C、9桶 D、10桶8. 如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为 , 若AB=1,BC=2,则阴影部分的面积为( )
A、7桶 B、8桶 C、9桶 D、10桶8. 如图,将矩形ABCD绕点A逆时针旋转90°至矩形AEFG,点D的旋转路径为 , 若AB=1,BC=2,则阴影部分的面积为( ) A、+ B、1+ C、 D、+1
A、+ B、1+ C、 D、+1二、填空题
-
9. 25的算术平方根是 .10. 分解因式: = .11. 函数y= 的自变量x的取值范围是 .12. 如果实数 , 满足方程组 , 那么.13. 半径为3,圆心角为的扇形的弧长为.14. 如图,点、、都在格点上,则的正切值为.
 15. 甲乙两台机床生产同一种零件,并且每天产量相等,在6天众每天生产零件中的次品数依次是:甲:3、0、0、2、0、1、;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是.16. 如图,中, , , 为中点.、是边、上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止.当为时,的面积最大.
15. 甲乙两台机床生产同一种零件,并且每天产量相等,在6天众每天生产零件中的次品数依次是:甲:3、0、0、2、0、1、;乙:1、0、2、1、0、2.则甲、乙两台机床中性能较稳定的是.16. 如图,中, , , 为中点.、是边、上的动点,从出发向运动,同时以相同的速度从出发向运动,运动到停止.当为时,的面积最大.
三、解答题
-
17.(1)、计算:;(2)、化简:.18. 解不等式组: , 并把它的解集在数轴上表示出来.
 19. 如图,点、、、在一条直线上, , , , 请写出与之间的位置关系,并证明你的结论.
19. 如图,点、、、在一条直线上, , , , 请写出与之间的位置关系,并证明你的结论.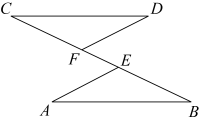 20. 某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
20. 某校为了解“阳光体育”活动的开展情况,从全校1000名学生中,随机抽取部分学生进行问卷调查(每名学生只能从A、B、C、D中选择一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
A:踢毽子 B:乒乓球 C:篮球 D:跳绳

根据以上信息,解答下列问题:
(1)、被调查的学生共有 ▲ 人,并补全条形统计图;(2)、在扇形统计图中,求表示区域D的扇形圆心角的度数;(3)、全校学生中喜欢篮球的人数大约是多少人?21. 某公司打算购买一批相同数量的玻璃杯和保温杯,计划用2000元购买玻璃杯,用2800元购买保温杯.已知一个保温杯比一个玻璃杯贵10元,求一个玻璃杯的价格.22. 从2名男生和2名女生中随机抽取运动会志愿者.(1)、随机抽取1名,恰好是女生的概率为;(2)、请用画树状图或列表的方法,写出抽取2名,恰好是1名男生和1名女生的概率.23. 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.(结果保留整数,参考数据:sin35°≈ ,cos35°≈ ,tan35°≈ , ≈1.7)
 24. 同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示.
24. 同时点燃甲乙两根蜡烛,蜡烛燃烧剩下的长度y(cm)与燃烧时间x(min)的关系如图所示. (1)、求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;(2)、求点P的坐标,并说明其实际意义;(3)、求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.25. 如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C.
(1)、求乙蜡烛剩下的长度y与燃烧时间x的函数表达式;(2)、求点P的坐标,并说明其实际意义;(3)、求点燃多长时间,甲蜡烛剩下长度是乙蜡烛剩下长度的1.1倍.25. 如图,DC是⊙O的直径,点B在圆上,直线AB交CD延长线于点A,且∠ABD=∠C. (1)、求证:AB是⊙O的切线;(2)、若AB=4cm,AD=2cm,求CD的长.26. 【背景】
(1)、求证:AB是⊙O的切线;(2)、若AB=4cm,AD=2cm,求CD的长.26. 【背景】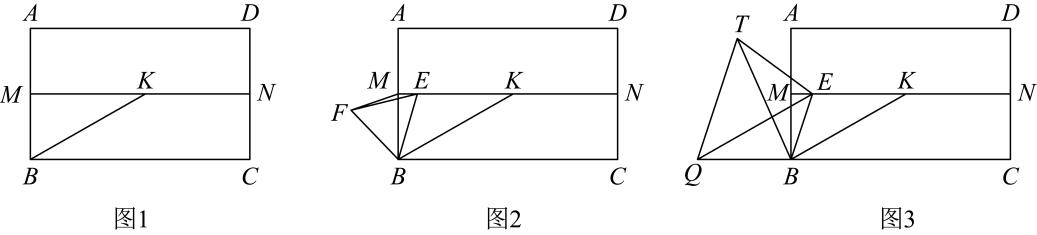
如图1,矩形中, , , 、分别是、的中点,折叠矩形使点落在上的点处,折痕为.
(1)、【操作】用直尺和圆规在图1中的边上作出点(不写作法,保留作图痕迹);(2)、【应用】求的度数和的长;(3)、如图2,若点是直线上的一个动点.连接 , 在左侧作等边三角形 , 连接 , 则的最小值是 ;(4)、【拓展】如图3,若点是射线上的一个动点.将沿翻折,得 , 延长至 , 使 , 连接.当是直角三角形时,的长为多少?请直接写出答案:.27. 如图,在中, , , , M是AB上的动点不与A、B重合 , 过点M作交AC于点N,以MN为直径作 , 并在内作内接矩形设.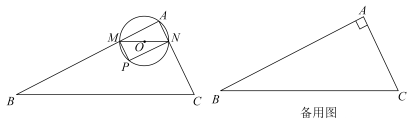 (1)、的面积 , ;用含x的代数式表示(2)、在动点M的运动过程中,设与四边形MNCB重合部分的面积为试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
(1)、的面积 , ;用含x的代数式表示(2)、在动点M的运动过程中,设与四边形MNCB重合部分的面积为试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?