江苏省常州市2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 点关于原点的对称点是( )A、 B、 C、 D、2. 方程 的解是( )A、x = 0 B、x = 2 C、x1= 0,x2= 1 D、x1= 0,x2= 23. 若线段a=2cm,线段b=8cm,则a,b的比例中项c为( )A、4cm B、5cm C、6cm D、32cm4. ⊙O的半径为6cm,圆心O到直线l的距离为7cm,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、不能确定5. 九(1)班45名同学一周课外阅读时间统计如表所示,那么该班45名同学一周课外阅读时间的众数、中位数分别是( )
人数(人)
5
19
15
6
时间(小时)
6
7
9
10
A、7,7 B、19,8 C、10,7 D、7,86. 如图,在中,弦 , 相交于点P, , , 则的度数为( ) A、 B、 C、 D、7. 在平面直角坐标系中,若点的横坐标与纵坐标的和为零,则称点为“零和点”.已知二次函数的图像上有且只有一个“零和点”,则下列结论正确的是( )A、 B、 C、 D、8. 如图,直线与轴、轴分别相交于点A、 , 过点作 , 使.将绕点顺时针旋转,每次旋转.则第2024次旋转结束时,点的对应点落在反比例函数的图象上,则的值为( )
A、 B、 C、 D、7. 在平面直角坐标系中,若点的横坐标与纵坐标的和为零,则称点为“零和点”.已知二次函数的图像上有且只有一个“零和点”,则下列结论正确的是( )A、 B、 C、 D、8. 如图,直线与轴、轴分别相交于点A、 , 过点作 , 使.将绕点顺时针旋转,每次旋转.则第2024次旋转结束时,点的对应点落在反比例函数的图象上,则的值为( ) A、6 B、-6 C、-4 D、4
A、6 B、-6 C、-4 D、4二、填空题
-
9. 在函数y= 中,自变量x的取值范围是 .10. 若 , 则 .11. 若关于的方程(为常数)有两个相等的实数根,则.12. 已知圆锥的底面半径为4cm,母线长为5cm,则圆锥的侧面积为 cm213. 在一个不透明的盒子中装有10个大小相同的乒乓球,做了1000次摸球试验,摸到红球的频数是400,估计盒子中的红球的个数是.14. 中, , , , 则的长是.15. 下表中两个变量y与x的数据满足我们初中学过的二次函数关系:
…
-1
0
1
3
…
…
0
3
4
0
…
则这个二次函数图象的对称轴为.
16. 如图,在边长为的正方形网格中,、、、为格点,连接、相交于点 , 则的长为.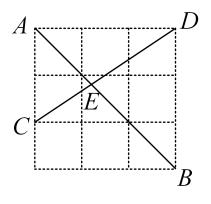 17. 如图,是等边三角形,边在轴上,反比例函数的图象经过点 , 若 , 点的坐标为 , 则k的值为.
17. 如图,是等边三角形,边在轴上,反比例函数的图象经过点 , 若 , 点的坐标为 , 则k的值为. 18. 图1是一个正方形网格,两条网格线的交点叫做格点.甲、乙两人在网格中进行游戏,规则如下:
18. 图1是一个正方形网格,两条网格线的交点叫做格点.甲、乙两人在网格中进行游戏,规则如下:
游戏规则a.两人依次在网格中画线段,线段的起点和终点均为格点;
b.新画线段的起点为前一条线段的终点,且与任意已画出线段不能有其它公共点;
c.已画出线段的所有端点中,任意三个端点不能在同一条直线上;
d.当某人无法画出新的线段时,则另一人获胜.
如图2,甲先画出线段 , 乙随后画出线段.若这局游戏继续进行下去,最终的获胜者是.(填“甲”,“乙”或“不确定”).

三、解答题
-
19. 计算:.20. 解方程:(1)、;(2)、.21. 某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调直,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其它项目(每位同学仅选一项),根据调查结果绘制了如下不完整的频数分布表和扇形统计图.
运动项目
频数(人数)
频率
篮球
30
0.25
羽毛球
m
0.20
乒乓球
36
n
跳绳
18
0.15
其它
12
0.10
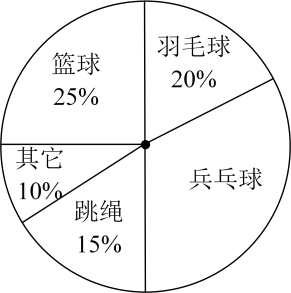
请根据以上图表信息,解答下列问题:
(1)、频数分布表中的m= , n= , “乒乓球”所在的扇形的圆心角的度数为;(2)、若该校有1000名学生,请估计最喜爱乒乓球这项运动的学生人数.22. 进出校园测量体温是学校常态化疫情防控的重要举措,学校有A、B两个测温通道,甲、乙、丙三个同学上学进校园,随机选择一个通道测量体温,(1)、甲同学通过A通道进入校园的概率是;(2)、请用列表或画树状图的方法求出甲、乙、丙三个同学经过同一个通道进校园的概率.23. 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D. (1)、以AB边上一点O为圆心,过A,D两点作⊙O;(用圆规、直尺作图,不写作法,但要保留作图痕迹)(2)、判断直线BC与⊙O的位置关系,并说明理由.24. 某小区门口安装了汽车出入道闸.道闸关闭时,如图①,四边形为矩形,长6米,长2米,点距地面为0.4米.道闸打开的过程中,边固定,连杆 , 分别绕点A,D转动,且边始终与边平行.如图②,当道闸打开至时,边上一点到地面的距离为2.4米,求点到的距离的长;
(1)、以AB边上一点O为圆心,过A,D两点作⊙O;(用圆规、直尺作图,不写作法,但要保留作图痕迹)(2)、判断直线BC与⊙O的位置关系,并说明理由.24. 某小区门口安装了汽车出入道闸.道闸关闭时,如图①,四边形为矩形,长6米,长2米,点距地面为0.4米.道闸打开的过程中,边固定,连杆 , 分别绕点A,D转动,且边始终与边平行.如图②,当道闸打开至时,边上一点到地面的距离为2.4米,求点到的距离的长; 25. 已知直线过点.点为直线上一点,其横坐标为.过点作轴的垂线,与函数的图象交于点.
25. 已知直线过点.点为直线上一点,其横坐标为.过点作轴的垂线,与函数的图象交于点. (1)、求的值;(2)、①求点的坐标(用含的式子表示);
(1)、求的值;(2)、①求点的坐标(用含的式子表示);②若的面积等于3,求出点的横坐标的值.
26. 如图,点是中边上一点,以为直径的与相切于点 , 连接. (1)、判断与是否相似?并说明理由。(2)、若的半径为3, , 求的长度.27. 在平面直角坐标系中,、为平面内不重合的两个点,若到、两点的距离相等,则称点是线段的“似中点”.
(1)、判断与是否相似?并说明理由。(2)、若的半径为3, , 求的长度.27. 在平面直角坐标系中,、为平面内不重合的两个点,若到、两点的距离相等,则称点是线段的“似中点”. (1)、已知 , , 在点、、中,线段的“似中点”是点;(2)、直线与轴交于点 , 与轴交于点.
(1)、已知 , , 在点、、中,线段的“似中点”是点;(2)、直线与轴交于点 , 与轴交于点.①求在坐标轴上的线段的“似中点”;
②若的半径为2,圆心在轴上,坐标为 , 上存在线段的“似中点”,请直接写出的取值范围.
28. 如图,抛物线经过、、三点,对称轴与抛物线相交于点、与相交于点 , 与轴交于点 , 连接. (1)、求该抛物线的解析式;(2)、抛物线上是否存在一点 , 使与的面积相等,若存在,请求出点的坐标;若不存在,说明理由.(3)、抛物线上存在一点 , 使 , 请直接写出点的坐标;
(1)、求该抛物线的解析式;(2)、抛物线上是否存在一点 , 使与的面积相等,若存在,请求出点的坐标;若不存在,说明理由.(3)、抛物线上存在一点 , 使 , 请直接写出点的坐标;