贵州省黔南州惠水县2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 下列实数中是无理数的是( )A、 B、 C、0 D、-12. 如图是由4个相同的小立方体搭成的几何体,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 2022年,我国就业、物价形势保持总体稳定脱贫劳动力务工规模超过3200万人,实现了巩固拓展脱贫攻坚成果同乡村振兴有效衔接.3200这个数用科学记数法可表示为( )A、 B、 C、 D、4. 如图, , , , 则的度数是( )
3. 2022年,我国就业、物价形势保持总体稳定脱贫劳动力务工规模超过3200万人,实现了巩固拓展脱贫攻坚成果同乡村振兴有效衔接.3200这个数用科学记数法可表示为( )A、 B、 C、 D、4. 如图, , , , 则的度数是( ) A、 B、 C、 D、5. 在一不透明的箱子里放有个除颜色外其他完全相同的球,其中只有4个白球,任意摸出一个球记下颜色后,放回袋中,再摇匀,再摸,通过大量重复摸球后发现,摸到白球的频率稳定在0.25,则大约是( )A、15 B、16 C、12 D、86. 分式 , 则的值是( )A、 B、 C、 D、7. 为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )
A、 B、 C、 D、5. 在一不透明的箱子里放有个除颜色外其他完全相同的球,其中只有4个白球,任意摸出一个球记下颜色后,放回袋中,再摇匀,再摸,通过大量重复摸球后发现,摸到白球的频率稳定在0.25,则大约是( )A、15 B、16 C、12 D、86. 分式 , 则的值是( )A、 B、 C、 D、7. 为了解“睡眠管理”落实情况,某初中学校随机调查50名学生每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖关于睡眠时间的统计量中,与被遮盖的数据无关的是( )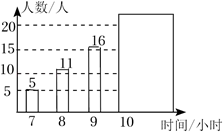 A、平均数 B、中位数 C、众数 D、方差8. 如图,边长相等的正五边形、正六边形的一边重合,则的度数为( )
A、平均数 B、中位数 C、众数 D、方差8. 如图,边长相等的正五边形、正六边形的一边重合,则的度数为( ) A、 B、 C、 D、9. 已知一元二次方程式的两根为、 , 且 , 求之值为何?( )A、9 B、-3 C、 D、10. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )
A、 B、 C、 D、9. 已知一元二次方程式的两根为、 , 且 , 求之值为何?( )A、9 B、-3 C、 D、10. 如图,在 中,分别以点 和点 为圆心,大于 长为半径画弧,两弧相交于点 , .作直线 ,交 于点 ,交 于点 ,连接 .若 , , ,则 的周长为( )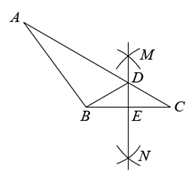 A、25 B、22 C、19 D、1811. 已知点在一次函数的图象上,且在一次函数图象的下方,则符合条件的值可能是( )A、-2 B、-1 C、0 D、112. 将一个长为20,宽为的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,得到如图所示的矩形,沿所得矩形两邻边中点的连线虚线剪下,再打开,得到如图所示的图形则图的面积是( )
A、25 B、22 C、19 D、1811. 已知点在一次函数的图象上,且在一次函数图象的下方,则符合条件的值可能是( )A、-2 B、-1 C、0 D、112. 将一个长为20,宽为的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,得到如图所示的矩形,沿所得矩形两邻边中点的连线虚线剪下,再打开,得到如图所示的图形则图的面积是( )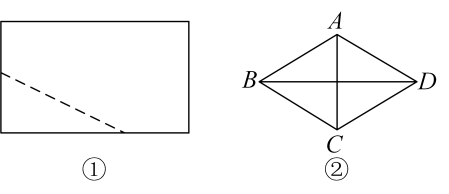 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
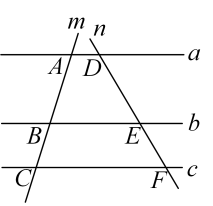
13. 因式分解: .14. 如图,直线 , 分别交直线、于点 , , , , , 若 , , 则的长为 .
 15. 秋天到了,花溪区高坡乡美景如画,其中露营基地吸引了不少露营爱好者,露营基地为了接待30名露营爱好者,需要搭建可容纳3人或2人的帐篷若干,若所搭建的帐篷恰好能容纳这30名露营爱好者,则不同的搭建方案有种.16. 在方格上建立平面直角坐标系如图所示,点绕坐标原点顺时针旋转后,恰好落在图中直角三角形阴影区域包括边界内,直角三角形顶点都在格点上,则的取值范围 .
15. 秋天到了,花溪区高坡乡美景如画,其中露营基地吸引了不少露营爱好者,露营基地为了接待30名露营爱好者,需要搭建可容纳3人或2人的帐篷若干,若所搭建的帐篷恰好能容纳这30名露营爱好者,则不同的搭建方案有种.16. 在方格上建立平面直角坐标系如图所示,点绕坐标原点顺时针旋转后,恰好落在图中直角三角形阴影区域包括边界内,直角三角形顶点都在格点上,则的取值范围 .
三、解答题
-
17.(1)、已知关于的不等式组 , 则这个不等式的解集为 .(2)、有一种电脑程序,每按一次按键,屏幕区就会自动加上 , 同时区就会自动减去 , 且均会显示化简后的结果已知 , 两区初始显示分别是和 , 如图所示.
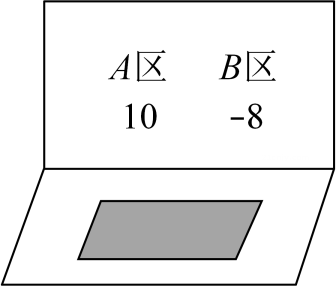
如:第一次按键后,A,两区分别显示

小红从初始状态按2次后,求A,两区代数式的和并化简,请判断这个和能为负数吗?说明理由.
18. 某校八年级计划在开学第二周的星期二至星期五开展社会实践活动,要求每位学生选择两天参加活动.(1)、乙同学随机选择连续的两天,其中有一天是星期三的概率是 ;(2)、甲同学随机选择两天,请用列表或画树状图的方法求其中有一天是星期三的概率.19. 如图,一次函数的图象与反比例函数的图象相交于、两点,点的坐标为. (1)、求出值并确定反比例函数的表达式;(2)、请直接写出当时,的取值范围.20. 在正方形中,是边上一点,在延长线上取点使过点作交于点 , 交于点交于点.
(1)、求出值并确定反比例函数的表达式;(2)、请直接写出当时,的取值范围.20. 在正方形中,是边上一点,在延长线上取点使过点作交于点 , 交于点交于点. (1)、求证:;(2)、若是的中点,请判断与的数量关系并说明理由.21. “献爱心”活动中,某班级两次选购同一种文具为偏远地区的贫困学生送去自己的爱心第一次用300元购买了一批,第二次购买时发现每件文具比第一次涨了2元,于是用800元购进了第二批文具,购买的数量是第一次购进数量的2倍.(1)、该班级第一次购买文具的单价是每件多少元?(2)、当卖家了解到学生的爱心行动后,捐出这两次售卖文具利润的60%给学生作为今后的爱心活动经费,已知卖家每件文具的进价都是5元,求该班级学生收到的经费是多少元?22. 如图,是某时刻太阳光线,光线与地面的夹角为小星身高米.
(1)、求证:;(2)、若是的中点,请判断与的数量关系并说明理由.21. “献爱心”活动中,某班级两次选购同一种文具为偏远地区的贫困学生送去自己的爱心第一次用300元购买了一批,第二次购买时发现每件文具比第一次涨了2元,于是用800元购进了第二批文具,购买的数量是第一次购进数量的2倍.(1)、该班级第一次购买文具的单价是每件多少元?(2)、当卖家了解到学生的爱心行动后,捐出这两次售卖文具利润的60%给学生作为今后的爱心活动经费,已知卖家每件文具的进价都是5元,求该班级学生收到的经费是多少元?22. 如图,是某时刻太阳光线,光线与地面的夹角为小星身高米. (1)、若小星正站在水平地面上处时,那么他的影长为多少米?(2)、若小星来到一个倾斜角为的坡面底端处,当他在坡面上至少前进多少米时,他的影子恰好都落在坡面上?23. 如图,、是圆上的两点, , 是的中点.
(1)、若小星正站在水平地面上处时,那么他的影长为多少米?(2)、若小星来到一个倾斜角为的坡面底端处,当他在坡面上至少前进多少米时,他的影子恰好都落在坡面上?23. 如图,、是圆上的两点, , 是的中点. (1)、求证:平分;(2)、延长至 , 使得 , 连接 , 若圆的半径 , 求的长.24. 已知抛物线.(1)、抛物线的顶点坐标为;(2)、当时,的最大值为18,求出的值;(3)、在(2)的条件下,若 , 是抛物线上两点,其中 , 记抛物线在、之间的部分为图像包含、两点 , 当、两点在抛物线的对称轴的两侧时,图像上最高点与最低点的纵坐标之差为2,求的取值范围.25. 如图,平行四边形中, , 点是边上的一点,连接 , 以为对称轴作的轴对称图形.
(1)、求证:平分;(2)、延长至 , 使得 , 连接 , 若圆的半径 , 求的长.24. 已知抛物线.(1)、抛物线的顶点坐标为;(2)、当时,的最大值为18,求出的值;(3)、在(2)的条件下,若 , 是抛物线上两点,其中 , 记抛物线在、之间的部分为图像包含、两点 , 当、两点在抛物线的对称轴的两侧时,图像上最高点与最低点的纵坐标之差为2,求的取值范围.25. 如图,平行四边形中, , 点是边上的一点,连接 , 以为对称轴作的轴对称图形.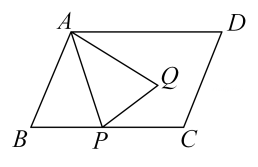
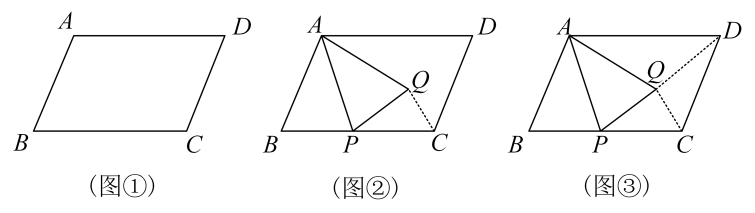 (1)、动手操作
(1)、动手操作当点正好落在边上时,在图①中画出的轴对称图形 , 并判断四边形的形状是 ▲ ;
(2)、问题解决如图②,当点是线段中点,且时,求的长;
(3)、拓展探究如图③,当点、、在同一直线上,且时,求的长.