四川省绵阳市江油市2023年中考一模数学试题
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、3. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
4. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )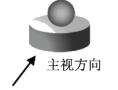 A、
A、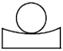 B、
B、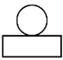 C、
C、 D、
D、 5. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,46. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( )
5. 《义务教育课程标准(2022年版)》首次把学生学会炒菜纳入劳动教育课程,并做出明确规定.某班有7名学生已经学会炒的菜品的种数依次为:3,5,4,6,3,3,4,则这组数据的众数和中位数分别是( )A、3,4 B、4,3 C、3,3 D、4,46. 如图, 的内切圆 与 分别相切于点D , E , F , 连接 , , , , ,则阴影部分的面积为( ) A、 B、 C、 D、7. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、8. 已知方程 , 且关于x的不等式只有2个整数解,那么b的取值范围是( )A、 B、 C、 D、9. 某市严格落实国家节水政策,2018年用水总量为6.5亿立方米,2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x,那么x满足的方程是( )A、 B、 C、 D、10. 如图,菱形的对角线相交于点O,过点D作于点H,连接 , 若 , , 则的长( )
A、 B、 C、 D、7. 某班级计划举办手抄报展览,确定了“5G时代”、“北斗卫星”、“高铁速度”三个主题,若小明和小亮每人随机选择其中一个主题,则他们恰好选择同一个主题的概率是( )A、 B、 C、 D、8. 已知方程 , 且关于x的不等式只有2个整数解,那么b的取值范围是( )A、 B、 C、 D、9. 某市严格落实国家节水政策,2018年用水总量为6.5亿立方米,2020年用水总量为5.265亿立方米.设该市用水总量的年平均降低率是x,那么x满足的方程是( )A、 B、 C、 D、10. 如图,菱形的对角线相交于点O,过点D作于点H,连接 , 若 , , 则的长( ) A、 B、 C、 D、11. 如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A、 B、 C、 D、11. 如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( ) A、 B、 C、 D、12. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.则下列结论正确的有( )
A、 B、 C、 D、12. 如图,已知开口向下的抛物线与x轴交于点 , 对称轴为直线.则下列结论正确的有( )①;
②函数的最大值为;
③若关于x的方程无实数根,则;
④代数式.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算.14. 如图,平行线 , 被直线所截,平分 , 若 , 则的度数是=.
 15. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= .
15. 如图,平行四边形OABC的顶点O是坐标原点,A在x轴的正半轴上,B,C在第一象限,反比例函数的图象经过点C,的图象经过点B.若 , 则k= . 16. 如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距米的C、D两点,测得 , .河的宽度是米.
16. 如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距米的C、D两点,测得 , .河的宽度是米. 17. 如图,在中, , 点D为的中点,将绕点D逆时针旋转得到 , 当点A的对应点落在边上时,点在的延长线上,连接 , 若 , 则的面积是 .
17. 如图,在中, , 点D为的中点,将绕点D逆时针旋转得到 , 当点A的对应点落在边上时,点在的延长线上,连接 , 若 , 则的面积是 . 18. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当时,.
18. 如图,点I为的内心,连接并延长交的外接圆于点D,点E为弦的中点,连接 , , , 当时,.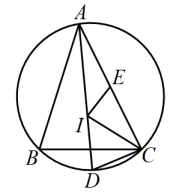
三、解答题
-
19.(1)、计算:(2)、先化简,再求值: , 其中.20. 2022年7月,教育部印发的《大中小学劳动教育指导纲要(试行)》中明确要求中小学劳动教育课平均每周不少于1课时,初中生平均每周劳动时间不少于3小时某初级中学为了解学生劳动教育的情况,从本校学生中随机抽取了500名进行问卷调查如图是根据此次调查结果得到的统计图.

请根据统计图回答下列问题:
(1)、本次调查中,平均每周劳动时间符合教育部要求的人数占被调查人数的百分比为多少?(2)、若该校有3000名学生,请估计最喜欢的劳动课程为木工的有多少人.(3)、请你根据本次问卷调查的结果给学校各提一条合理化建议.21. 如图,已知直线与反比例函数的图象交于点 , 直线经过点A,且与l关于直线对称.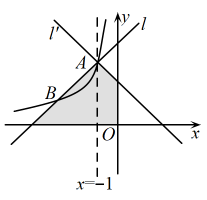 (1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.(3)、已知直线与反比例函数的图象交于点另一点B,P在在平面内,若以点A,B,P,O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.22. 如图,已知四边形ABCD为矩形 , ,点E在BC上, ,将△ABC沿AC翻折到△AFC,连接EF.
(1)、求反比例函数的解析式;(2)、求图中阴影部分的面积.(3)、已知直线与反比例函数的图象交于点另一点B,P在在平面内,若以点A,B,P,O为顶点的四边形是平行四边形,请直接写出所有符合条件点P的坐标.22. 如图,已知四边形ABCD为矩形 , ,点E在BC上, ,将△ABC沿AC翻折到△AFC,连接EF. (1)、求EF的长;(2)、求sin∠CEF的值.23. 学校计划组织初二年级200名师生到红军烈士陵园举行清明扫墓纪念活动.现需租用A,B两种型号的客车共10辆,两种型号客车的载客量(不包括司机)和租金信息如下表:
(1)、求EF的长;(2)、求sin∠CEF的值.23. 学校计划组织初二年级200名师生到红军烈士陵园举行清明扫墓纪念活动.现需租用A,B两种型号的客车共10辆,两种型号客车的载客量(不包括司机)和租金信息如下表:型号
载客量(人/辆)
租金单价(元/辆)
A
16
900
B
22
1200
若设租用A型客车x辆,租车总费用为y元.
(1)、请写出y与x的函数关系式(不要求写自变量取值范围):(2)、据资金预算,本次租车总费用不超过11800元,则A型客车至少需租几辆?(3)、在(2)的条件下,要保证全体师生都有座位,问有哪几种租车方案?请选出最省钱的租车方案.

