四川省成都市彭州市、都江堰市等5地2023年九年级中考一模数学试题

试卷更新日期：2023-04-27 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{7}{8}$ 的倒数是（）

A、 $- \frac{7}{8}$ B、 $\frac{7}{8}$ C、 $- \frac{8}{7}$ D、 $\frac{8}{7}$

查看试题解析
2. 据第三方大数据监测显示，某年春节期间四川省共接待游客 $5387.59$ 万人次，旅游收入242亿元，同比分别增长 $24.73 ％$ ， $10.43 ％$ ，增幅超过全国平均水平.将数据242亿用科学记数法表示为（）

A、 $2.42 \times 1 0^{2}$ B、 $2.42 \times 1 0^{9}$ C、 $2.42 \times 1 0^{10}$ D、 $2.42 \times 1 0^{11}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \cdot a^{3} = 2 a^{3}$ C、 ${(- 2 a b^{3})}^{2} = 4 a^{2} b^{5}$ D、 $(- a + 1) (a + 1) = 1 - a^{2}$

查看试题解析
4. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 是 $∠ A$ 角平分线， $D E ⊥ A B$ 于点E， $C D = 2$ ， $B C = 6$ ，则 $B E =$ （）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、6

查看试题解析
5. 如图是根据某次射击比赛中甲、乙两人5次射击的成绩（环数）制作的折线统计图，成绩更稳定的是（）

A、甲 B、一样 C、乙 D、不能确定

查看试题解析
6. 如图，直线 $A B ， C D$ 相交于点O， $E O ⊥ C D$ ，垂足为点O.若 $∠ 1 = 52 °$ ，则 $∠ 2$ 的度数为（）

A、 $28 °$ B、 $38 °$ C、 $52 °$ D、 $42 °$

查看试题解析
7. 《九章算术》中记载了一个问题，大意是：有几个人一起去买一件物品，每人出9元，多5元；每人出6元，少4元.问：有多少人？该物品价值多少元？设有x人，物品价值y元，则所列方程组正确的是（）

A、 ${\begin{array}{l} 9 x - 5 = y \\ 6 x - 4 = y \end{array}$ B、 ${\begin{array}{l} 9 x + 5 = y \\ 6 x - 4 = y \end{array}$ C、 ${\begin{array}{l} 9 x - 5 = y \\ 6 x + 4 = y \end{array}$ D、 ${\begin{array}{l} 9 x + 5 = y \\ 6 x + 4 = y \end{array}$

查看试题解析
8. 下列关于抛物线 $y = x^{2} + 4 x - 5$ 的说法正确的是（）
①开口方向向上；②对称轴是直线 $x = - 4$ ；③当 $x < - 2$ 时，y随x的增大而减小；④当 $x < - 5$ 或 $x > 1$ 时， $y > 0$ .

A、①③ B、①④ C、①③④ D、①②③④

查看试题解析

二、填空题

9. 因式分解：3x²+6x+3= ．

查看试题解析
10. 计算： $\sqrt{{(- 999)}^{2}} =$ .

查看试题解析
11. 若关于x的一元二次方程 $m x^{2} + n x - 1 = 0$ （ $m \neq 0$ ）的一个解是 $x = - 1$ ，则 $m - n =$ .

查看试题解析
12. 如果两个相似三角形的面积之比为 $1 ： 4$ ，这两个三角形的周长的和是 $60 c m$ ，那么小的三角形的周长为 $c m$ .

查看试题解析
13. 如图，四边形 $A B C D$ 是平行四边形，以点B为圆心， $B C$ 的长为半径作弧交 $A D$ 于E，分别以点C，E为圆心，大于 $\frac{1}{2} C E$ 的长为半径作弧，两弧交于点P，作射线 $B P$ 交 $A D$ 的延长线于点F， $B C = 4 \sqrt{2}$ ，则 $E F =$ .

查看试题解析

三、解答题

14.

(1)、计算： ${(2023 - 5 \sqrt{3})}^{0} - | 2 - \sqrt{12} | + {(\frac{1}{2})}^{- 2} + 4 c o s 30 °$

(2)、先化简，再求值： $\frac{x^{2} - 2 x + 1}{x^{2} + x} \div (1 - \frac{2}{x + 1})$ ，其中 $x ＝ - 2$ .

查看试题解析
15. 某校为进一步活跃校园文化活动，促进学生体育社团活动向健康、文明、向上的方向发展，优化育人环境，全面抓好学生社团工作，更加合理地安排体育社团活动，学校请某班数学兴趣小组就本班同学“我最想加入的体育社团”进行了一次调查统计，下面是小组通过收集数据后绘制的两幅不完整的统计图.
请你根据图中提供的信息，解答以下问题：

(1)、该班共有多少名学生？在扇形统计图中，“其他”部分所对应的圆心角度数是多少度？请补全条形统计图；

(2)、全市举行学生乒乓球比赛，该学校要推选5位乒乓球社团同学参加，其中有2名七年级同学 $（ A ， B ）$ 和3名八年级同学 $（ C ， D ， E ）$ ，现从中选取两名同学组成双打组合，用树状图或列表法表示出所有的结果，并求出恰好抽到七，八年同学各1名的概率.

查看试题解析
16. 如图，小茗家车库的宽 $A B$ 长为3米，小茗妈妈将一辆宽为 $1.8$ 米（即 $M N = 1.8$ 米）的汽车正直停入车库，此时 $M N ∥ A B$ ，车门 $C D$ 长为 $1.2$ 米，当左侧车门 $C D$ 接触到墙壁时，车门与车身的夹角 $∠ C D E$ 为 $45 °$ ，此时 $F G$ 为右侧车门开至最大的宽度（也是物体进出的最大宽度），小茗妈妈能否将车内一个边长为40厘米的正方体包裹从右侧车门取出？（结果精确到 $0.01$ 米；参考数据： $\sqrt{2} \approx 1.414$ ）

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点O为 $A B$ 边上一点，以 $O A$ 为半径的 $⊙ O$ 与 $B C$ 相切于点D，分别交 $A B$ ， $A C$ 边于点E，F.

(1)、证明： $A D$ 平分 $∠ B A C$ ；

(2)、若 $B D = \frac{4}{3}$ ， $t a n ∠ C A D = \frac{1}{2}$ ，求 $⊙ O$ 的半径.

查看试题解析
18. 如图，在平面直角坐标系中，四边形 $A B C D$ 为正方形，已知点 $A (- 6 ， 0)$ 、 $D (- 7 ， 3)$ ，点 $B$ 、 $C$ 在第二象限内.

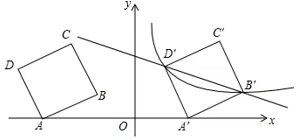(1)、点 $B$ 的坐标；

(2)、将正方形 $A B C D$ 以每秒2个单位的速度沿 $x$ 轴向右平移 $t$ 秒，若存在某一时刻 $t$ ，使在第一象限内点 $B$ 、 $D$ 两点的对应点 $B^{'}$ 、 $D^{'}$ 正好落在某反比例函数的图象上，请求出此时 $t$ 的值以及这个反比例函数的解析式；

(3)、在（2）的情况下，问是否存在 $y$ 轴上的点 $P$ 和反比例函数图象上的点 $Q$ ，使得以 $P$ 、 $Q$ 、 $B^{'}$ 、 $D^{'}$ 四个点为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点 $Q$ 的坐标；若不存在，请说明理由.

查看试题解析

四、填空题

19. 若 ${(x - 1)}^{2} = 2$ ，则代数式 $3 x^{2} - 6 x - 5 =$ .

查看试题解析
20. 将二次函数 $y = 2 x^{2} - 8 x + 13$ 化成 $y = a (x + h)^{2} + k$ 的形式为.

查看试题解析
21. 在平面直角坐标系中，如果一个点的横坐标与纵坐标互为相反数，则称该点为“黎点”.例如 $(- 1 ， 1)$ ， $(2023 ， - 2023)$ 都是“黎点”.若抛物线 $y = a x^{2} - 9 x + c$ （ $a ， c$ 为常数）上有且只有一个“黎点”，当 $a > 1$ 时，c的取值范围是.

查看试题解析
22. 如图，在矩形 $A B C D$ 中， $A B = 3 ， A D = 4$ ， E，F分别是边 $B C ， C D$ 上的点， $E F ⊥ A E$ ，将 $△ E C F$ 沿 $E F$ 翻折得到 $△ E C^{'} F$ ，连接 $A C^{'}$ ，当 $△ A E C^{'}$ 是以 $A E$ 为腰的等腰三角形时， $B E =$ .

查看试题解析
23. 如图， $△ A B C ∽ △ A D E$ ， $∠ B A C = ∠ D A E = 90 °$ ， $A B = 5$ ， $A C = 12$ ， F为 $D E$ 中点，若点D在直线 $B C$ 上运动，连接 $C F$ ，则在点D运动过程中，线段 $C F$ 的最小值为.

查看试题解析

五、解答题

24. “儿童散学归来早，忙趁东风放纸鸢”，阳春三月，正是放风筝的好时节，某商店购进一批风筝.已知成批购进时的单价是30元.调查发现：销售单价是40元时，月销售量是300件，而销售单价每上涨1元，月销售量就减少10件，但每个风筝售价不能高于60元.设每个风筝的销售单价上涨了x元时（x为正整数），月销售利润为y元.

(1)、求y与x的函数关系式并直接写出自变量x的取值范围；

(2)、每个风筝的售价定为多少元时可使月销售利润最大？最大的月销售利润是多少？

查看试题解析
25. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于点 $A (- 1 ， 0)$ ，点 $B (3 ， 0)$ ，与y轴交于点 $C (0 ， - 3)$ .

(1)、求抛物线的函数表达式；

(2)、在对称轴上找一点Q，使 $△ A Q C$ 的周长最小，求点Q的坐标；

(3)、在（2）的条件下，点P是抛物线上的一点，当 $△ A Q C$ 和 $△ A Q P$ 面积相等时，请求出所有点P的坐标.

查看试题解析
26.

(1)、【探究发现】如图，在正方形 $A B C D$ 中，E为 $A D$ 边上一点，将 $△ A E B$ 沿BE翻折得到 $△ B E F$ ，延长 $E F$ 交 $C D$ 边于点G.求证： $△ B F G ≅ △ B C G$ ；

(2)、【类比迁移】如图，在矩形 $A B C D$ 中，E为 $A D$ 边上一点，且 $A D = 8 ， A B = 6$ ，将 $△ A E B$ 沿 $B E$ 翻折得到 $△ B E F$ ，延长 $E F$ 交 $B C$ 边于点G，延长 $B F$ 交 $C D$ 边于点H，且 $F H = C H$ ，求 $A E$ 的长；

(3)、【实践创新】如图， $R t △ A B C$ 为等腰三角形， $∠ A B C = 90 °$ ， O为斜边 $A C$ 的中点， M，N为线段 $A C$ 上的动点，且满足 $∠ M B N = 45 °$ ，设 $∠ M B O = α$ ， $∠ N B O = β$ ， $A B = \sqrt{2}$ ，证明： $t a n (α + β) = \frac{t a n α + t a n β}{1 - t a n α \cdot t a n β}$ .

查看试题解析