陕西省西安市未央区2023年中考数学模拟试卷
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、3 B、 C、 D、12. 如图将一块三角板如图放置, ,点 分别在 上,若 ,则 的度数为( )
 A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 矩形具有而菱形不具有的性质是( )A、对边相等 B、对角线互相垂直 C、邻边垂直 D、对角线互相平分5. 如图,在中, , D、E分别是的中点,连接 , 若 , , 则点A到的距离是( )
A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 矩形具有而菱形不具有的性质是( )A、对边相等 B、对角线互相垂直 C、邻边垂直 D、对角线互相平分5. 如图,在中, , D、E分别是的中点,连接 , 若 , , 则点A到的距离是( ) A、 B、 C、10 D、126. 如图,是在同一坐标系内作出的一次函数、的图象,设 , , 则方程组的解是( )
A、 B、 C、10 D、126. 如图,是在同一坐标系内作出的一次函数、的图象,设 , , 则方程组的解是( )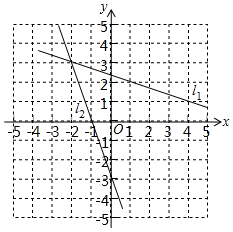 A、 B、 C、 D、7. 如图,已知在中, , 且 , 则的度数为( )
A、 B、 C、 D、7. 如图,已知在中, , 且 , 则的度数为( ) A、 B、 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
A、 B、 C、 D、8. 下表中列出的是一个二次函数的自变量x与函数y的几组对应值:x
…
0
1
3
…
y
…
6
…
下列选项中,正确的是( )
A、这个函数的开口向下 B、这个函数的图象与x轴无交点 C、当时,y的值随x的增大而减小 D、这个函数的最小值小于6二、填空题
-
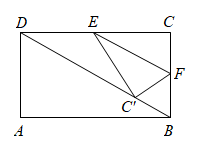
9. 计算:.10. 的大小顺序是(用“>”号连接).11. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐到足底的长度之比约是黄金分割比.著名的“断臂维纳斯”便是如此.若某人的身体满足上述黄金分割比,且身高为175cm,则此人的肚脐到足底的长度约是(精确到1cm).12. 点A(2,1)在反比例函数的图象上,当1<y<4时,x的取值范围是 .13. 如图,在矩形中, , , 点为线段的中点,动点从点出发,沿的方向在和上运动,将矩形沿折叠,点的对应点为 , 当点恰好落在矩形的对角线上时,点运动的距离为.
三、解答题
-
14. 计算:.15. 解不等式组并写出该不等式组的最小整数解.16. 计算(1)、(2)、17. 如图,点E、F分别是上的点,连接 , 分别交于点G、H,若 , , 求证:.
 18. 如图,在中, , D、E分别为、上一点,.若 , 求证:.
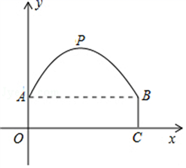
18. 如图,在中, , D、E分别为、上一点,.若 , 求证:.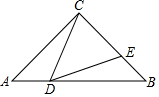 19. 一个四边形的形状和尺寸如图1所示.建立适当的直角坐标系,在坐标系中作出这个四边形,并标出各顶点的坐标.
19. 一个四边形的形状和尺寸如图1所示.建立适当的直角坐标系,在坐标系中作出这个四边形,并标出各顶点的坐标. 20. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.21. 小明和小华利用学过的知识测量操场旗杆的高度,测量时,小明让小华站在点B处,此时,小华影子的顶端E与旗杆的影子C顶端重合,且的长为2米;小明又让小华沿着射线的方向走15.2米到达旗杆的另一侧N处,此时,小华观测到旗杆顶端C的仰角为 , 已知小华的身高为1.8米,请你根据相关测量信息,计算旗杆的高度.
20. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.21. 小明和小华利用学过的知识测量操场旗杆的高度,测量时,小明让小华站在点B处,此时,小华影子的顶端E与旗杆的影子C顶端重合,且的长为2米;小明又让小华沿着射线的方向走15.2米到达旗杆的另一侧N处,此时,小华观测到旗杆顶端C的仰角为 , 已知小华的身高为1.8米,请你根据相关测量信息,计算旗杆的高度. 22. 下图是一个运算程序:
22. 下图是一个运算程序: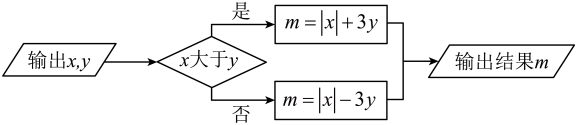 (1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.23. 为了解学生参加户外活动的情况,某中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
(1)、若 , , 求的值;(2)、若 , 输出结果的值是输入的值的两倍,求的值.23. 为了解学生参加户外活动的情况,某中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题: (1)、被抽样调查的学生有 人,并补全条形统计图.(2)、每天户外活动2小时对应的圆心角度数是.(3)、该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?24. 如图,已知点A、D、C、F在同一条直线上, , .给出下列三个条件:① , ② , ③.
(1)、被抽样调查的学生有 人,并补全条形统计图.(2)、每天户外活动2小时对应的圆心角度数是.(3)、该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?24. 如图,已知点A、D、C、F在同一条直线上, , .给出下列三个条件:① , ② , ③. (1)、请在上述三个条件中选取一个条件,使得.你选取的条件序号为 , 你判定的依据是(填“”或“”或“”或“”);(2)、请用(1)中所选条件证明;(3)、可看作是由沿方向平移得到的,过B作于M,当 , , 是以为腰的等腰三角形时,直接写出平移距离的长.
(1)、请在上述三个条件中选取一个条件,使得.你选取的条件序号为 , 你判定的依据是(填“”或“”或“”或“”);(2)、请用(1)中所选条件证明;(3)、可看作是由沿方向平移得到的,过B作于M,当 , , 是以为腰的等腰三角形时,直接写出平移距离的长.