陕西省西安市临潼区2023年中考数学模拟试卷
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 圆柱的侧面展开图是下列图形中的( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,将菱形纸片沿着线段剪成两个全等的图形,则的度数是( ) A、40° B、60° C、80° D、100°5. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、40° B、60° C、80° D、100°5. 如图, 中, ,点D在 上, .若 ,则 的长度为( )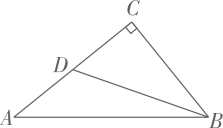 A、 B、 C、 D、46. 在平面直角坐标系中,若将一次函数的图象向右平移个单位后,得到一个正比例函数的图象,则m的值为( )A、 B、 C、 D、7. 如图,四边形 内接于 , , 为 中点, ,则 等于( )
A、 B、 C、 D、46. 在平面直角坐标系中,若将一次函数的图象向右平移个单位后,得到一个正比例函数的图象,则m的值为( )A、 B、 C、 D、7. 如图,四边形 内接于 , , 为 中点, ,则 等于( )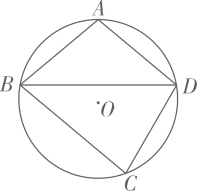 A、 B、 C、 D、8. 二次函数的顶点坐标为 , 其部分图象如图所示.以下结论错误的是( )
A、 B、 C、 D、8. 二次函数的顶点坐标为 , 其部分图象如图所示.以下结论错误的是( ) A、 B、 (m为任意实数) C、 D、关于x的方程无实数根
A、 B、 (m为任意实数) C、 D、关于x的方程无实数根二、填空题
-
9. 比较大小:3 (填<,>或=).10. 正八边形的一个内角的度数是 度。
11. “方程”二字最早见于我国《九章算术》这部经典著作中,该书的第八章名为“方程”如: 从左到右列出的算筹数分别表示方程中未知数 , 的系数与相应的常数项,即可表示方程 , 则
从左到右列出的算筹数分别表示方程中未知数 , 的系数与相应的常数项,即可表示方程 , 则 表示的方程是. 12. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上.反比例函数y=(x<0)的图象经过菱形对角线的交点A,若点D的坐标为(-3,4),则k等于 .
表示的方程是. 12. 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上.反比例函数y=(x<0)的图象经过菱形对角线的交点A,若点D的坐标为(-3,4),则k等于 . 13. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.
13. 如图,在中, , , , 半径为1的在内平移(可以与该三角形的边相切),则点到上的点的距离的最大值为.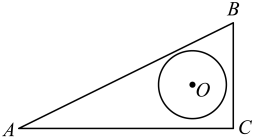
三、解答题
-
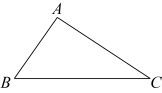
14. 计算:.15. 解不等式组:.16. 解方程:.17. 如图,已知锐角三角形 , 用尺规作图法在上作一点 , 使得.(保留作图痕迹,不写作法)
 18. 已知:如图,在ABC中,三角形的两条高AH,CG交于点F且AG=CG,求证:GF=GB.
18. 已知:如图,在ABC中,三角形的两条高AH,CG交于点F且AG=CG,求证:GF=GB. 19. 某商场举办促销活动,本次活动中的家电消费券单笔交易满600元立减60元(每次只能使用一张).某品牌电饭煲按进价提高50%后标价,若按标价的八折销售,当某顾客购买该电饭煲时,使用一张家电消费券后,又付现金636元,求该电饭煲的进价.
19. 某商场举办促销活动,本次活动中的家电消费券单笔交易满600元立减60元(每次只能使用一张).某品牌电饭煲按进价提高50%后标价,若按标价的八折销售,当某顾客购买该电饭煲时,使用一张家电消费券后,又付现金636元,求该电饭煲的进价. 20. “双减”政策下,为了切实提高课后服务质量,阳光中学开展了丰富多彩的课后服务活动,设置了:“A.体育活动,B.劳动技能,C.经典阅读,D.科普活动”四大板块课程,若该校晶晶和强强随机选择一个板块课程.(1)、晶晶选“体育活动”课程的概率是 ;(2)、用画树状图或列表的方法,求晶晶和强强选相同板块课程的概率.21. 如图,某城市的一座古塔CD坐落在湖边,数学老师带领学生隔湖测量古塔CD的高度,在点A处测得塔尖点D的仰角∠DAC为31°,沿射线AC方向前进35米到达湖边点B处,测得塔尖点D在湖中的倒影E的俯角∠CBE为45°,根据测得的数据,计算这座灯塔的高度CD(结果精确到0.1).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.(结果精确到0.1)
20. “双减”政策下,为了切实提高课后服务质量,阳光中学开展了丰富多彩的课后服务活动,设置了:“A.体育活动,B.劳动技能,C.经典阅读,D.科普活动”四大板块课程,若该校晶晶和强强随机选择一个板块课程.(1)、晶晶选“体育活动”课程的概率是 ;(2)、用画树状图或列表的方法,求晶晶和强强选相同板块课程的概率.21. 如图,某城市的一座古塔CD坐落在湖边,数学老师带领学生隔湖测量古塔CD的高度,在点A处测得塔尖点D的仰角∠DAC为31°,沿射线AC方向前进35米到达湖边点B处,测得塔尖点D在湖中的倒影E的俯角∠CBE为45°,根据测得的数据,计算这座灯塔的高度CD(结果精确到0.1).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.(结果精确到0.1)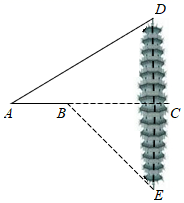 22. 涛涛同学骑共享单车保持匀速从家到博学书店买书,选好书付好款后,以相同的速度原路骑共享单车返回家中.设涛涛同学距离家的路程为 , 运动时间为 , y与x之间的函数图象如图所示.
22. 涛涛同学骑共享单车保持匀速从家到博学书店买书,选好书付好款后,以相同的速度原路骑共享单车返回家中.设涛涛同学距离家的路程为 , 运动时间为 , y与x之间的函数图象如图所示.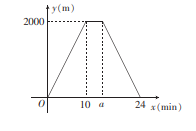 (1)、 .(2)、在涛涛同学从书店返回家的过程中,求y与x之间的函数关系式.(3)、在涛涛从家里出发的同时,小波同学以60m/min的速度从博学书店匀速步行去涛涛家,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间.23. 某学校开展了“学党史、知党恩、跟党走”的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行党史知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等第:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).
(1)、 .(2)、在涛涛同学从书店返回家的过程中,求y与x之间的函数关系式.(3)、在涛涛从家里出发的同时,小波同学以60m/min的速度从博学书店匀速步行去涛涛家,当小波同学与涛涛同学在路上相遇时,直接写出涛涛同学的运动时间.23. 某学校开展了“学党史、知党恩、跟党走”的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行党史知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等第:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如图统计图(部分信息未给出).

由图中给出的信息解答下列问题:
(1)、求测试成绩为合格的学生人数,并补全频数直方图.(2)、求扇形统计图中“良好”所对应的扇形圆心角的度数.(3)、如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?24. 如图,⊙O是△ABC的外接圆,AE平分∠BAC交⊙O于点E,交BC于点D,过点E作直线l∥BC. (1)、判断直线l与⊙O的位置关系,并说明理由;(2)、若∠ABC的平分线BF交AD于点F,求证:BE=EF;25. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为 .
(1)、判断直线l与⊙O的位置关系,并说明理由;(2)、若∠ABC的平分线BF交AD于点F,求证:BE=EF;25. 某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线第一象限部分的函数表达式为 . (1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.26.(1)、请在图中过点A画一条直线,将分成面积相等的两部分;
(1)、求雕塑高OA.(2)、求落水点C,D之间的距离.(3)、若需要在OD上的点E处竖立雕塑EF, , .问:顶部F是否会碰到水柱?请通过计算说明.26.(1)、请在图中过点A画一条直线,将分成面积相等的两部分; (2)、如图,在平行四边形中,请过顶点A画两条直线将平行四边形的面积三等分,并说明理由;
(2)、如图,在平行四边形中,请过顶点A画两条直线将平行四边形的面积三等分,并说明理由; (3)、如图,农博园有一块四边形空地,其中 , , , , , 点P为边的中点.春天到了,百花齐放,农博园设计部门想在这片空地上种三种不同的花卉,要求三种花卉的种植面积相等,现规划,从入口P处修两条笔直的小路(小路的面积忽略不计)方便游客赏花,两条小路将这块地的面积三等分,请通过计算、画图说明设计部门能否实现规划,若能,请确定小路尽头的位置;若不能,请说明理由.
(3)、如图,农博园有一块四边形空地,其中 , , , , , 点P为边的中点.春天到了,百花齐放,农博园设计部门想在这片空地上种三种不同的花卉,要求三种花卉的种植面积相等,现规划,从入口P处修两条笔直的小路(小路的面积忽略不计)方便游客赏花,两条小路将这块地的面积三等分,请通过计算、画图说明设计部门能否实现规划,若能,请确定小路尽头的位置;若不能,请说明理由.