陕西省西安市蓝田县2023年中考数学一模试卷
试卷更新日期:2023-04-27 类型:中考模拟
一、单选题
-
1. ﹣9的相反数是( )A、9 B、﹣9 C、 D、﹣2. 如图, , .若 , 则的大小为( )
 A、 B、 C、 D、3. 计算:( )A、 B、 C、 D、4. 下列条件不能够判定“平行四边形是菱形”的是( )A、 B、 C、 D、5. 如图,是的高,若 , 则( )
A、 B、 C、 D、3. 计算:( )A、 B、 C、 D、4. 下列条件不能够判定“平行四边形是菱形”的是( )A、 B、 C、 D、5. 如图,是的高,若 , 则( ) A、 B、2 C、 D、6. 以二元一次方程的解为坐标的点都在一次函数的图像上,则常数a的值为( )A、 B、 C、 D、7. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )
A、 B、2 C、 D、6. 以二元一次方程的解为坐标的点都在一次函数的图像上,则常数a的值为( )A、 B、 C、 D、7. 如图,正五边形内接于 , 点F在弧上.若 , 则的大小为( )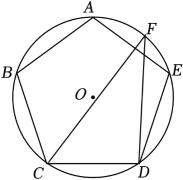 A、38° B、42° C、48° D、58°8. 已知抛物线 , 当时,y的最小值为 , 则当时,y的最大值为( )A、2 B、1 C、0 D、
A、38° B、42° C、48° D、58°8. 已知抛物线 , 当时,y的最小值为 , 则当时,y的最大值为( )A、2 B、1 C、0 D、二、填空题
-
9. 计算:.10. 实数a、b在数轴上对应的点如图所示,则0.(填“”“”“”)
 11. 我国三国时期的杰出数学家赵爽在注解《周髀算经》时,巧妙地运用弦图证明了勾股定理.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的两条直角边分别是2和4,则中间小正方形的面积占大正方形面积的.
11. 我国三国时期的杰出数学家赵爽在注解《周髀算经》时,巧妙地运用弦图证明了勾股定理.“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的两条直角边分别是2和4,则中间小正方形的面积占大正方形面积的. 12. 若点A在反比例函数上,点A关于y轴的对称点B在反比例函数上,则的值为.13. 如图,在正方形中, , 点分别为边上的点,且 , 点分别在上,且 , 则的长为.
12. 若点A在反比例函数上,点A关于y轴的对称点B在反比例函数上,则的值为.13. 如图,在正方形中, , 点分别为边上的点,且 , 点分别在上,且 , 则的长为.
三、解答题
-
14. 计算: .15. 解不等式组.16. 化简:.17. 如图,已知.请用尺规作图法,在边上找一点E,使得.(保留作图痕迹,不写作法).
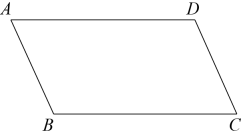 18. 如图,在矩形中,F是的中点,连接交延长线于点E.求证:.
18. 如图,在矩形中,F是的中点,连接交延长线于点E.求证:. 19. 如图,的顶点坐标分别为.
19. 如图,的顶点坐标分别为. (1)、在图中作出关于x轴的对称图形;(2)、若将向右平移3个单位得到 , 则点B的对应点的坐标是.20. 甲、乙两位同学玩抽卡片游戏,游戏规则如下:在大小和形状完全相同的4张卡片上分别标上数字2、4、4、5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字,然后将卡片放回搅匀.(1)、甲同学从这4张卡片中随机抽取一张,则抽到标有数字4的卡片的概率是;(2)、甲、乙两位同学各抽取卡片一次,若取出的两张卡片数字之和为3的倍数,则甲胜;否则乙胜.请用列表或画树状图的方法说明这个游戏规则对双方是否公平.21. 小明晚上路过一个羽毛球场,场地的周围是平坦的草坪.他想测量场地旁边路灯的高度,但是没有带任何测量工具.他发现路灯与羽毛球网在同一平面,于是,小明调整自己的步伐,尽量使得每一步步长相同.小明测出离路灯较近的网杆在路灯下的影长为2步,离路灯较远的网杆在路灯下的影长为5步.回家后小明上网查资料得到羽毛球网杆高米,网长米,同时测得1步米.已知 , , , 垂足分别为点B、D、E.求路灯的高.(结果保留一位小数)
(1)、在图中作出关于x轴的对称图形;(2)、若将向右平移3个单位得到 , 则点B的对应点的坐标是.20. 甲、乙两位同学玩抽卡片游戏,游戏规则如下:在大小和形状完全相同的4张卡片上分别标上数字2、4、4、5,将这4张卡片放入一个不透明盒子中搅匀,参与者每次从中随机抽取一张卡片,记录数字,然后将卡片放回搅匀.(1)、甲同学从这4张卡片中随机抽取一张,则抽到标有数字4的卡片的概率是;(2)、甲、乙两位同学各抽取卡片一次,若取出的两张卡片数字之和为3的倍数,则甲胜;否则乙胜.请用列表或画树状图的方法说明这个游戏规则对双方是否公平.21. 小明晚上路过一个羽毛球场,场地的周围是平坦的草坪.他想测量场地旁边路灯的高度,但是没有带任何测量工具.他发现路灯与羽毛球网在同一平面,于是,小明调整自己的步伐,尽量使得每一步步长相同.小明测出离路灯较近的网杆在路灯下的影长为2步,离路灯较远的网杆在路灯下的影长为5步.回家后小明上网查资料得到羽毛球网杆高米,网长米,同时测得1步米.已知 , , , 垂足分别为点B、D、E.求路灯的高.(结果保留一位小数) 22. 如图,是一个“函数求值机”示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.
22. 如图,是一个“函数求值机”示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.
输入x
…
0
2
…
输出y
…
19
15
11
0
8
…
根据以上信息,解答下列问题:
(1)、当输入的x值为时,输出的y值为;(2)、求k2 , b的值;(3)、当输出的y值为24时,求输入的x值.23. 在一次社会调查活动中,小亮收集到某公司“健步走运动”团队中20名成员某一天行走的步数,并进行统计,绘制了如下统计表:组别
步数分组
频数
组内成员的平均步数
A
B
C
D
E
根据上述信息,解答下列问题:
(1)、这名“健步走运动”团队成员这一天行走的步数的中位数落在组;(2)、求这名“健步走运动”团队成员这一天行走的平均步数;(3)、若该团队共有人,请估计在该团队所有成员中,这一天行走步数不少于步的人数.24. 如图,为的弦,直线与相切于点C,且 , 连接并延长交于点D,交于点E. (1)、求证:;(2)、若 , 求的半径.
(1)、求证:;(2)、若 , 求的半径.

