贵州省遵义市新蒲新区2023年中考一模数学试题

试卷更新日期：2023-04-27 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $| - 2 |$ 的结果为（）

A、2 B、 $- 2$ C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 汇川区依托政策和区位优势，位于“一带一路”和长江经济带核心腹地，通过大力发展智能制造、生物医药、高新技术，整体经济实力得到明显提升，2022年上半年的经济总量就已经达到 $230.88$ 亿元.数据 $230.88$ 亿元用科学记数法表示为 $a \times 1 0^{^{n}}$ 元的形式，则 $n$ 的值为（）

A、2 B、5 C、8 D、10

查看试题解析
3. 剪纸文化是中国最古老的民间艺术之一，在下图中依次是“福、禄、寿、喜、财”五个字的艺术剪纸，若将这五张图片打乱顺序后全部装入一个不透明的盒子中，从中随机抽取一张，抽到的图案中的文字是中心对称图形的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
4. 小华想用老师提供的三条线段首尾相连围成一个直角三角形，则他应该选择的三条线段长度是（）

A、 $2$ 、 $3$ 、 $4$ B、 $3$ 、 $4$ 、 $5$ C、 $4$ 、 $5$ 、 $6$ D、 $5$ 、 $6$ 、 $7$

查看试题解析
5. 下列计算正确的是（）

A、 ${(- m)}^{7} \div {(- m)}^{2} = - m^{5}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 ${(3 x y^{2})}^{2} = 6 x^{2} y^{4}$ D、 ${(a^{2} b)}^{2} = a^{2} b^{2}$

查看试题解析
6. 将一把直尺和一块含 $30 °$ 角的直角三角板按如图所示方式摆放，其中 $∠ C B D = 90 °$ ， $∠ B D C = 30 °$ ，若 $∠ 1 = 78 °$ ，则 $∠ 2$ 的度数为（）

A、 $12 °$ B、 $18 °$ C、 $42 °$ D、 $48 °$

查看试题解析
7. 下列说法正确的是（）

A、调查中央电视台《开学第一课》的收视率，应采用全面调查的方式 B、数据3，5，4，1，2的中位数是4 C、“清明时节雨纷纷”是必然事件 D、甲、乙两名射击运动员10次射击成绩（单位：环）的平均数相等，方差分别为 ${S_{甲}}^{2} = 0.4$ ， ${S_{乙}}^{2} = 2$ ，则甲的成绩比乙的稳定

查看试题解析
8. 设a，b是方程 $x^{2} + x - 2023 = 0$ 的两个不相等的实数根，则 $\frac{a^{2} + a b}{a}$ 的值为（）

A、1 B、 $- 1$ C、2023 D、 $- 2023$

查看试题解析
9. 在显示汽车油箱内油量的装置模拟示意图中，电压 $U$ 一定时，油箱中浮子随油面下降而落下，带动滑杆使滑动变阻器滑片向上移动，从而改变电路中的电流，电流表的示数对应油量体积，把电流表刻度改为相应油量体积数，由此知道油箱里剩余油量．在不考虑其他因素的条件下，油箱中油的体积 $V$ 与电路中总电阻 $R_{总} （ R_{总} = R + R_{0} ）$ 是反比例关系，电流 $I$ 与 $R_{总}$ 也是反比例关系，则 $I$ 与 $V$ 的函数关系是（）

A、反比例函数 B、正比例函数 C、二次函数 D、以上答案都不对

查看试题解析
10. 如图，正方形网格中每个小正方形的边长均为 $1$ ，其中，B、C、D、E四点都在网格的格点上，则 $△ A B C$ 的面积为（）

A、 $7.5$ B、 $8$ C、 $\frac{25}{3}$ D、 $8.5$

查看试题解析
11. 如图，菱形 $A B C D$ 的边长为 $2$ ， $∠ B = 120 °$ ，点P是对角线 $A C$ 上的一个动点，点E、F分别为边 $A D$ 、 $D C$ 的动点，则 $P E + P F$ 的最小值是（）

A、 $2$ B、 $1.5$ C、 $\sqrt{5}$ D、 $\sqrt{3}$

查看试题解析
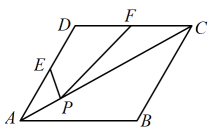12. 函数 $y = | a x^{2} + b x + c | (a > 0 ， b^{2} - 4 a c > 0)$ 的图象是由函数 $y = a x^{2} + b x + c (a > 0 ， b^{2} - 4 a c > 0)$ 的图象x轴上方部分不变，下方部分沿x轴向上翻折而成，如图所示，则下列结论正确的是（）
① $2 a + b = 0$ ；② $c = 3$ ；③ $a b c > 0$ ；④将图象向上平移 $1$ 个单位后与直线 $y = 5$ 有 $3$ 个交点

A、①② B、①③ C、①③④ D、②③

查看试题解析

二、填空题

13. 在函数 $y = \frac{3}{2 - x}$ 中，自变量x的取值范围是.

查看试题解析
14. 2023年3月12日是我国第45个植树节，某林业部门为了考察某种幼树在一定条件下的移植成活率，在同等条件下，对这种幼树进行大量移植，并统计成活情况，下表是这种幼树移植过程中的一组统计数据：
幼树移植数（棵）
100
1000
5000
8000
10000
15000
20000
幼树移植成活数（棵）
87
883
4455
7209
8983
13519
18044
幼树移植成活的频率
0.8700
0.8820
0.8910
0.9011
0.8983
0.9013
0.9022
估计该种幼树在此条件下移植成活率是.（结果精确到 $1 %$ ）

查看试题解析
15. 把量角器和含 $30 °$ 角的三角板按如图方式摆放：零刻度线与长直角边重合，移动量角器使外圆弧与斜边相切时，发现中心恰好在刻度2处，短直角边过量角器外沿刻度120处（即 $O C = 2 c m$ ， $∠ B O F = 120 °$ ）.则阴影部分的面积为.

查看试题解析
16. 如图，正方形 $A B C D$ 的中心与坐标原点O重合，将顶点 $D (1 ， 0)$ 绕点 $A (0 ， 1)$ 逆时针旋转 $90 °$ 得点 $D_{1}$ ，再将 $D_{1}$ 绕点 $B$ 逆时针旋转 $90 °$ 得点 $D_{2}$ ，再将 $D_{2}$ 绕点C逆时针旋转 $90 °$ 得点 $D_{3}$ ，再将 $D_{3}$ 绕点D逆时针旋转 $90 °$ 得点 $D_{4}$ ，再将 $D_{4}$ 绕点A逆时针旋转 $90 °$ 得点 $D_{5}$ ……依此类推，则点 $D_{2023}$ 的坐标是.

查看试题解析

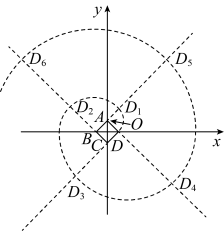
三、解答题

17. 计算： $\sqrt{12} - 4 c o s 30 ° + {(3.14 - π)}^{0} + | 1 - \sqrt{2} |$ .

查看试题解析
18. 先化简，再求值 $\frac{x - 2}{x - 1} \div (x + 1 - \frac{3}{x - 1})$ .其中x的值是一元二次方程 $x^{2} + 2 x - 3 = 0$ 的解.

查看试题解析
19. 贵州省遵义市凤凰楼，位于凤凰山主峰，该楼为一幢七层六角型仿古景观建筑，游客登上楼顶后，可以将遵义城区风景一览无余，是当地识别性很高的地标建筑.在一次综合实践活动中，某小组对凤凰楼的楼高进行了如下测量.如图，将测角仪放在楼前平坝C处测得该楼顶端B的仰角为 $60 °$ ，沿平坝向后退 $50 m$ $(C D = 50 m)$ 到D处有一棵树，将测角仪放在距地面 $2 m$ $(D E = 2 m)$ 的树枝上的E处，测得B的仰角为 $30 °$ .请你帮助该小组计算凤凰楼的高度 $A B$ .（结果精确到 $1 m$ ，参考数据： $\sqrt{3} \approx 1.73$ ）

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，一次函数 $y = a x + b$ 的图象与反比例函数 $y = \frac{k}{x}$ 的图象都经过 $A (2 ， - 4) 、 B (- 4 ， m)$ 两点．

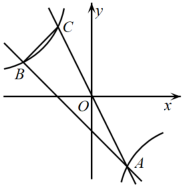(1)、求反比例函数和一次函数的表达式；

(2)、过O、A两点的直线与反比例函数图象交于另一点C，连接BC，求 $△ A B C$ 的面积．

查看试题解析
21. 如图，下列装在相同的透明密封盒内的古钱币，其密封盒上分别标有古钱币的尺寸及质量，例如：钱币“文星高照”密封盒上所标“ $45.4 * 2.8 m m$ ， $24.4 g$ ”是指该枚古钱币的直径为 $45.4 m m$ ，厚度为 $2.8 m m$ ，质量为 $24.4 g$ .已知这些古钱币的材质相同.
根据图中信息，解决下列问题.

(1)、这5枚古钱币，所标直径的平均数是mm，所标厚度的众数是mm，所标质量的中位数是 g.

(2)、由于古钱币无法从密封盒内取出，为判断密封盒上所标古钱币的质量是否有错，桐桐用电子秤测得每枚古钱币与其密封盒的总质量如下：
名称
文星高照
状元及第
鹿鹤同春
顺风大吉
连中三元
总质量/ $g$
58.7
58.1
55.2
54.3
55.8
盒标质量
24.4
24.0
13.0
20.0
21.7
盒子质量
34.3
34.1
42.2
34.3
34.1
请你应用所学的统计知识，判断哪枚古钱币所标的质量与实际质量差异较大，并计算该枚古钱币的实际质量约为多少克.

查看试题解析
22. 随着北京冬奥会的召开，冬奥会吉祥物成为了热门商品.某店购买了冰墩墩和雪容融两种吉祥物毛绒玩具销售.已知冰墩墩的单价比雪容融的单价多10元，且用4900元买冰墩墩的数量与用4400元购买雪容融的数量相同.

(1)、冰墩墩和雪容融的单价各是多少元？

(2)、因为太畅销，该店还需要增加购买一批吉样物，增加购买的雪容融数量是冰墩墩数量的2倍，若总费用不超过50000元，则增加购买冰墩墩的数量最多是多少？

查看试题解析
23. 已知：如图， $A B$ 为 $⊙ O$ 的直径， $C D$ 与 $⊙ O$ 相切于点C，交 $A B$ 延长线于点D，连接 $A C$ ， $B C$ ， $∠ D = 30 °$ ， $C E$ 平分 $∠ A C B$ 交 $⊙ O$ 于点E，过点B作 $B F ⊥ C E$ ，垂足为F.

(1)、求证： $C A = C D$ ；

(2)、若 $A B = 12$ ，求线段 $B F$ 的长.

查看试题解析
24. 将抛物线 $C_{1}$ 向左平移1个单位长度，再向上平移4个单位长度得到抛物线 $C_{2} ： y = x^{2}$ .

(1)、直接写出抛物线 $C_{1}$ 的解析式；

(2)、如图，已知抛物线 $C_{1}$ 与x轴交于A，B两点，点A在点B的左侧，点 $P (2 ， t)$ 在抛物线 $C_{1}$ 上， $Q B ⊥ P B$ 交拋物线于点Q.求点Q的坐标；

查看试题解析
25.

(1)、【问题探究】如图1，在正方形 $A B C D$ 中，点E、F分别在边 $D C$ 、 $B C$ 上，且 $A E ⊥ D F$ ，求证： $A E = D F$ .

(2)、【知识迁移】如图2，在矩形 $A B C D$ 中， $A B = 3$ ， $B C = 4$ ，点E在边 $A D$ 上，点M、N分别在边 $A B$ 、 $C D$ 上，且 $B E ⊥ M N$ ，求 $\frac{B E}{M N}$ 的值.

(3)、【拓展应用】如图3，在平行四边形 $A B C D$ 中， $A B = m$ ， $B C = n$ ，点 $E 、 F$ 分别在边 $A D 、 B C$ 上，点M、N分别在边 $A B$ 、 $C D$ 上，当 $∠ E F C$ 与 $∠ M N C$ 的度数之间满足什么数量关系时，有 $\frac{E F}{M N} = \frac{m}{n}$ ？试写出其数量关系，并说明理由.

查看试题解析

幼树移植数（棵）	100	1000	5000	8000	10000	15000	20000
幼树移植成活数（棵）	87	883	4455	7209	8983	13519	18044
幼树移植成活的频率	0.8700	0.8820	0.8910	0.9011	0.8983	0.9013	0.9022

名称	文星高照	状元及第	鹿鹤同春	顺风大吉	连中三元
总质量/ $g$	58.7	58.1	55.2	54.3	55.8
盒标质量	24.4	24.0	13.0	20.0	21.7
盒子质量	34.3	34.1	42.2	34.3	34.1