山西省2022-2023学年八年级第二学期期中数学模拟试题人教版

试卷更新日期：2023-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 要使代数式 $\frac{x}{\sqrt{x + 1}}$ 有意义，则 $x$ 的取值范围是（）

A、 $x > - 1$ B、 $x \geq - 1$ C、 $x \neq 0$ D、 $x > - 1$ 且 $x \neq 0$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{4} = \pm 2$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $2 \sqrt{3} - \sqrt{3} = 2$ D、 $\sqrt{2} \cdot \sqrt{3} = \sqrt{6}$

查看试题解析
3. 如图，正方形ABCD的边长为4，点M在DC上，且DM=1，N是AC上一动点，则DN+MN的最小值为（）

A、4 B、 $4 \sqrt{2}$ C、 $2 \sqrt{5}$ D、5

查看试题解析
4. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）

A、b²＝（a+c）（a-c） B、∠A＝∠B+∠C C、∠A：∠B：∠C＝3：4：5 D、a＝6，b＝8，c＝10

查看试题解析
5. 如图，平行四边形ABCD中，P是形内任意一点，△ABP，△BCP，△CDP，△ADP的面积分别为S₁ ， S₂ ， S₃ ， S₄ ，则一定成立的是（）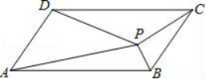

A、S₁+S₂＞S₃+S₄ B、S₁+S₂=S₃+S₄ C、S₁+S₂＜S₃+S₄ D、S₁+S₃=S₂+S₄

查看试题解析
6. 若一次函数y＝ax+b的图象经过第一、二、四象限，则 $\sqrt{a^{2}} - \sqrt{(b - a)^{2}} =$ （）

A、-2a-b B、2a-b C、-b D、-2a+b

查看试题解析
7. 设b＞a，将一次函数y₁＝ax+b与y₂＝bx+a的图象画在同一平面直角坐标系中，则有组a，b的取值，使得下列四个备选答案中有一个是正确的，则这个正确的答案是（）

A、 B、 C、 D、

查看试题解析
8. 有甲、乙两组数据，如下表所示：
甲
11
12
13
14
15
乙
12
12
13
14
14
两组数据的方差分别是 $s_{甲}^{2}$ 、 $s_{乙}^{2}$ ，则 $s_{甲}^{2}$ 与 $s_{乙}^{2}$ 的大小关系为（）

A、 $s_{甲}^{2} < s_{乙}^{2}$ B、 $s_{甲}^{2} > s_{乙}^{2}$ C、 $s_{甲}^{2} \leq s_{乙}^{2}$ D、 $s_{甲}^{2} \geq s_{乙}^{2}$

查看试题解析
9. 若点 $A (x_{1} ， - 1)$ ， $B (x_{2} ， - 2)$ ， $C (x_{3} ， 3)$ 在一次函数 $y = - 2 x + m$ （ $m$ 是常数）的图象上，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系是（）

A、 $x_{1} > x_{2} > x_{3}$ B、 $x_{2} > x_{1} > x_{3}$ C、 $x_{1} > x_{3} > x_{2}$ D、 $x_{3} > x_{2} > x_{1}$

查看试题解析
10. 如图，边长为4的正方形ABCD中，点E，F分别是边BC，DC上的点，且∠EAF=45°，下列结论：① $S_{Δ A B E} + S_{Δ A D F} = S_{Δ A E F}$ ；②BE+DF=EF；③当△ABE≌△ADF时，EF的长为 $8 \sqrt{2} - 8$ ；④当EF=4时，△CEF是等腰直角三角形，其中正确结论的个数是（）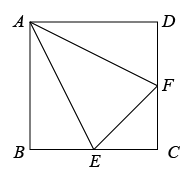

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 如图，根据图中的标注和作图痕迹可知，在数轴上的点A所表示的数为．

查看试题解析
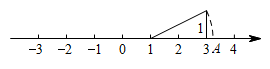12. 已知x＝2+ $\sqrt{5}$ ， y＝2- $\sqrt{5}$ ，则代数式x²+y²的值为．

查看试题解析
13. 小泽和小帅两同学分别从甲地出发，骑自行车沿同一条路到乙地参加社会实践活动．如图折线 $O A B$ 和线段 $C D$ 分别表示小泽和小帅离甲地的距离y（单位：千米）与时间x（单位：小时）之间函数关系的图象，则当小帅到达乙地时，小泽距乙地的距离为千米．

查看试题解析
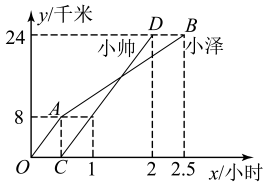14. 某少年军校准备从甲、乙、丙三位同学中选拔一个参加全市射击比赛.他们在选拔比赛中，射靶十次的平均环数是 $\bar{x_{甲}} = \bar{x_{乙}} = 8.3$ ， $\bar{x_{丙}} = 8$ ；方差分别是， ${s^{2}}_{甲} = 1.5$ ， ${s^{2}}_{乙} = 2.8$ ， ${s^{2}}_{丙} = 1.5$ ，那么根据以上提供的信息，你认为应该被推荐参加全市射击比赛的同学是.

查看试题解析
15. 汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”.如图，大正方形 $A B C D$ 由四个全等的直角三角形和一个小正方形组成，若 $∠ A D E = ∠ A E D$ ， $△ A D E$ 的面积为3，则 $A D =$ .

查看试题解析

三、解答题

16. 已知：如图，点E，F分别在 $▱ A B C D$ 的AB，DC边上，且 $A E = C F$ ，连接DE，BF.求证：四边形DEBF是平行四边形.

查看试题解析
17. 如图，正方形ABCD中，F为DC的中点，E为BC上一点，CE= $\frac{1}{4}$ BC，求证：∠AFE是直角.

查看试题解析
18. 在解决问题“已知a＝ $\frac{1}{\sqrt{2} - 1}$ ，求3a²﹣6a﹣1的值”时，小明是这样解答的：
∵a＝ $\frac{1}{\sqrt{2} - 1} = \frac{\sqrt{2} + 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \sqrt{2} + 1$ ，

∴a﹣1＝ $\sqrt{2}$ ，

∴（a﹣1）²＝2，即a²﹣2a+1＝2，

∴a²﹣2a＝1，

∴3a²﹣6a＝3，

∴3a²﹣6a﹣1＝2．

请你根据小明的解答过程，解决下面的问题：

若a＝ $\frac{2}{3 - \sqrt{7}}$ ，求2a²﹣12a+1的值．

查看试题解析
19. 每年6月5日是“世界环境日”，某小区为积极响应“共建清洁美丽世界”的号召，计划购进A，B两种树苗共60棵美化小区环境，已知A种树苗每棵130元，B种树苗每棵150元，若购进A种树苗的数量不多于B种树苗的两倍，则A，B两种树苗各购进多少棵时，费用最省？最省费用是多少？

查看试题解析
20. 某社区为了增强居民节约用水的意识，随机调查了部分家庭一年的月均用水量（单位：t）．根据调查结果，绘制出如下的统计图①和图②．

请根据相关信息，解答下列问题：

（Ⅰ）本次接受调查的家庭个数为，图①中m的值为；

（Ⅱ）求统计的这组月均用水量数据的平均数、众数和中位数．

查看试题解析

21. 【阅读材料】

老师的问题：

已知：如图， $A E ∥ B F$ ．

求作：菱形 $A B C D$ ，使点C，D分别在 $B F ， A E$ 上．

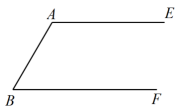
小明的作法：

（1）以A为圆心， $A B$ 长为半径画弧，交 $A E$ 于点D；

（2）以B为圆心， $A B$ 长为半经画弧，交 $B F$ 于点C；

（3）连接 $C D$ ．

四边形 $A B C D$ 就是所求作的菱形，

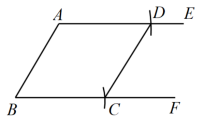
【解答问题】

请根据材料中的信息，证明四边形 $A B C D$ 是菱形．

查看试题解析

22. 定义：我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形．

(1)、【性质初探】如图1，已知 $▱$ ABCD，∠B＝80°，点E是边AD上一点，连结CE，四边形ABCE恰为等腰梯形．求∠BCE的度数；

(2)、【性质再探】如图2，已知四边形ABCD是矩形，以BC为一边作等腰梯形BCEF，BF＝CE，连结BE、CF．求证：BE＝CF；

(3)、【拓展应用】如图3， $▱$ ABCD的对角线AC、BD交于点Ｏ，AB＝2，∠ABC＝45°，过点Ｏ作AC的垂线交BC的延长线于点G，连结DG．若∠CDG＝90°，求BC的长．

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = - 2 x + 6$ 的图像分别交x轴，y轴于A，B两点，过点A的直线交y轴正半轴于点M，且BM=2MO．在平面直角坐标系内存在点C，使得以A，B，M，C为顶点的四边形是平行四边形，请你画出图形，确定点C的坐标．

查看试题解析

甲	11	12	13	14	15
乙	12	12	13	14	14

山西省2022-2023学年八年级第二学期期中数学模拟试题 人教版

一、单选题

二、填空题

三、解答题

山西省2022-2023学年八年级第二学期期中数学模拟试题人教版