人教版2023年中考数学模拟试卷（一）

试卷更新日期：2023-04-27 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣|﹣ $\frac{1}{2}$ |的倒数是（　　）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 一个几何体的主视图和俯视图如图所示，那么它的左视图可能是（）

A、 B、 C、 D、

查看试题解析
3. 我国是世界人口大国，中央高度重视粮食安全，要求坚决守住1 800 000 000亩耕地红线.将数据1 800 000 000用科学记数法表示为（）

A、 $18 \times 1 0^{8}$ B、 $1.8 \times 1 0^{9}$ C、 $0.18 \times 1 0^{10}$ D、 $1.8 \times 1 0^{10}$

查看试题解析
4. 如图，在正方形方格纸中，每个小正方形的边长都相等，A，B，C，D都在格点处，AB与CD相交于点P，则cos∠APC的值为（）

A、 $\frac{\sqrt{3}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{2}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
5. 若 $x^{2} + k x + 16 = {(x - 4)}^{2}$ ，那么（）

A、k=－8，从左到右是乘法运算 B、k=8，从左到右是乘法运算 C、k=－8，从左到右是因式分解 D、k=8，从左到右是因式分解

查看试题解析
6. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点坐标为 $(- 1 ， n)$ ，其部分图象如图所示，则以下结论错误的是（）

A、 $a b c > 0$ B、该二次函数的图象经过点 $(- 2 ， - c)$ C、 $3 a + c < 0$ D、关于x的方程 $a x^{2} + b x + c = n + 1$ 无实数根

查看试题解析
7. 如图，在边长为 $4$ 正方形 $A B C D$ 中，点 $E$ 在以 $B$ 为圆心的弧 $A C$ 上，射线 $D E$ 交 $A B$ 于 $F$ ，连接 $C E$ ，若 $C E ⊥ D F$ ，则 $D E$ =（）

A、 $2$ B、 $\frac{2}{5} \sqrt{5}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{6}{5} \sqrt{5}$

查看试题解析
8. 如图，电路图上有3个开关A，B，C和一个小灯泡，同时闭合开关A，C或同时闭合开关B，C都可以使小灯泡发光.下列操作中，使“小灯泡发光”的事件是随机事件的是（）

A、不闭合开关 B、只闭合1个开关 C、只闭合2个开关 D、闭合3个开关

查看试题解析
9. 如图，在菱形ABCD中，AE⊥BC于E，将△ABE沿AE所在直线翻折得△AEF，若AB＝2，∠B＝45°，则△AEF与菱形ABCD重叠部分（阴影部分）的面积为（）.

A、2 B、 $2 - \sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $2 \sqrt{2} - 2$

查看试题解析
10. 如图，矩形 $A B C D$ 中， $A B = 4$ ， $B C = 6$ ，点P是矩形 $A B C D$ 内一点，连接 $P A$ ， $P C$ ， $P D$ ，若 $P A ⊥ P D$ ，则 $P C$ 的最小值为（）

A、 $2 \sqrt{13} - 4$ B、 $2 \sqrt{10} - 3$ C、2 D、4

查看试题解析

二、填空题

11. 计算： $\sqrt{24} + \sqrt{6} =$ ．

查看试题解析
12. 超市用1200元钱批发了A，B两种西瓜进行销售，两种西瓜的批发价和零售价如下表所示，若计划将这批西瓜全部售完后，所获利润率不低于40%，则该超市至少批发A种西瓜 $k g$ ．
名称
A
B
批发价（元/ $k g$ ）
4
3
零售价（元/ $k g$ ）
6
4

查看试题解析
13. 某闭合电路中，电源的电压为定值，电流I（A）与电阻R（Ω）成反比例．如图表示的是该电路中电流I与电阻R之间函数关系的图象，当电阻R为6Ω时，电流I为 A．

查看试题解析
14. 关于x的一元二次方程 $(a - 2) x^{2} - 4 x + 1 = 0$ 有实数根，则a的取值范围是．

查看试题解析
15. 如图，正方形 $A B C D$ 中，P为边 $A D$ 上一点，点E与B关于直线 $C P$ 对称，射线 $E D$ 与 $C P$ 的延长线相交于点F.若 $A D = 4 P D$ ， $E F = 16 \sqrt{2}$ ，则 $B C$ 的长为 .

查看试题解析

三、计算题

16.

(1)、计算： $(- 1)^{4} \times | - 3 | + 2 \times {(\frac{1}{2})}^{- 3}$ ；

(2)、先化简，再求值： $(m + 2 - \frac{5}{m - 2}) \div \frac{3 m - m^{2}}{m - 2}$ ，其中 $m = 5$ ．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ B = 30 °$ ．

(1)、用尺规作图法作 $B C$ 边上的高 $A D$ ，垂足为D；

(2)、若 $A C$ 平分 $∠ B A D$ ，求证： $B C = 2 C D$ ．

查看试题解析

四、解答题

18. 某校积极响应国家号召，为落实垃圾“分类回收，科学处理”的政策，准备购买 $100$ L和 $240$ L两种型号的垃圾箱若干套．若购买8套 $100$ L垃圾箱和5套 $240$ L垃圾箱，共需7200元；若购买4套 $100$ L垃圾箱和6套 $240$ L垃圾箱，共需6400元．

(1)、每套 $100$ L垃圾箱和每套 $240$ L垃圾箱各多少元？

(2)、学校决定购买 $100$ L垃圾箱和 $240$ L垃圾箱共20套，且 $240$ L垃圾箱的数量不少于 $100$ L垃圾箱数量的 $\frac{1}{4}$ ，求购买这20套垃圾箱的最少费用．

查看试题解析
19. 某校开展数学周系列活动，举办了“测量”为主题的实践活动．小杰所在小组准备借助无人机来测量小区内的一座大楼高度．如图所示，无人机从地面点A处沿着与地面垂直的方向上升，至点B处时，测得大楼底部C的俯角为30°，测得大楼顶部D的仰角为45°．无人机保持航向不变继续上升50米到达点E处，此时测得大楼顶部D的俯角为45°．已知A，C两点在同一水平线上，根据以上信息，请帮小杰小组计算大楼的高度．（结果保留根号）

查看试题解析
20. 某中学为了解本校中考体育情况，随机抽取了部分学生的体育成绩进行统计分析，发现最低分为 45 分，且成绩为45分的学生占抽查人数的10%，现将抽查结果绘制成了如下不完整的折线统计图，请根据图中信息，回答下列问题：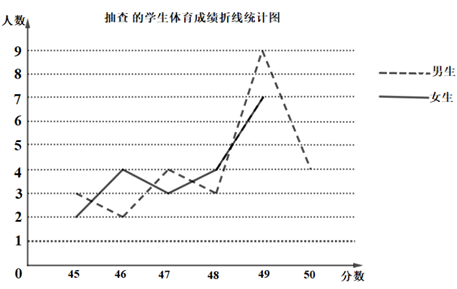

(1)、此次抽查的学生人数为人，抽查的学生体育考试成绩的中位数是分，抽查的女生体育考试成绩的平均数是分；

(2)、补全折线统计图；

(3)、为了今后中考体育取得更好的成绩，学校决定分别从成绩为50分的生和女生中各选一名参加“经验座谈会”，若成绩为50分的男、女生中各有两名体育特长生，请用列表或画树状图的方法求出所选的两名学生刚好都不是体育特长生的概率．

查看试题解析
21. 阅读材料：若 $x$ 满足 $(6 - x) (x - 4) = 3$ ，求 ${(6 - x)}^{2} + {(x - 4)}^{2}$ 的值．
解：设 $(6 - x) = a$ ， $(x - 4) = b$ ，则 $(6 - x) (x - 4) = a b = 3$ ， $a + b = (6 - x) + (x - 4) = 2$
所以 ${(6 - x)}^{2} + {(x - 4)}^{2} = a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 2^{2} - 2 \times 3 = - 2$
请仿照上例解决下列问题：

(1)、若x满足 $(20 - x) (x - 10) = - 5$ ，求 ${(20 - x)}^{2} + {(x - 10)}^{2}$ 的值；

(2)、若x满足 ${(2023 - x)}^{2} + {(2021 - x)}^{2} = 2022$ ，求 $(2023 - x) (2021 - x)$ 的值；

(3)、如图，正方形 $A B C D$ 的边长为 $x$ ， $A E = 2$ ， $F C = 4$ ，长方形 $E B F G$ 的面积是10，四边形 $H I B E$ 和 $B J K F$ 都是正方形， $I L J B$ 是长方形，求图中阴影部分的面积（结果必须是一个具体的数值）．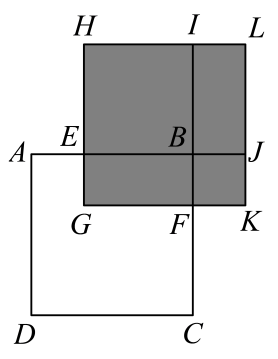

查看试题解析

五、综合题

22. 在矩形ABCD的CD边上取一点E，将△BCE沿BE翻折，得到△BFE．已知 $A B = 6$ ， $B C = 10$ ．

(1)、若点F恰好在AD上；
①如图1，过点F作 $F O ∥ C D$ 交BE于点O，求证：四边形FOCE为菱形．
②如图2，延长EF，与 $∠ A B F$ 的角平分线交于点M，BM交AD于点N．请猜想NF与BC的关系，并说明理由；

(2)、如图3，若点F不在AD上， $∠ A B F$ 的角平分线交EF的延长线于点M，点E从点C运动到点D的过程中，直接写出点M运动的路径长．

查看试题解析
23. 如图，已知二次函数 $y = - x^{2} + b x + c$ 的图象经过点 $A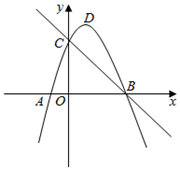 (- 1 ， 0) ， B (3 ， 0)$ ，与y轴交于点C.

(1)、求抛物线的解析式；

(2)、点D为抛物线的顶点，求 $△ B C D$ 的面积；

(3)、抛物线上是否存在点P，使 $∠ P A B = ∠ A B C$ ，若存在，请直接写出点P的坐标；若不存在，请说明理由.

查看试题解析

名称	A	B
批发价（元/ $k g$ ）	4	3
零售价（元/ $k g$ ）	6	4