吉林省长春市2022年5月中考模拟——数学试卷
试卷更新日期:2023-04-27 类型:中考模拟
一、选择题(本大题共8小题,每小题3分,共24分)
-
1. 互为相反数的两个数的和为( )A、0 B、正数 C、负数 D、无法确定2. 2022年3月23日下午,“天宫课堂”第二课在中国空间站开讲,由神舟十三号乘组航天员翟志刚、王亚平、叶光富在太空进行授课.央视新闻抖音号全程进行直播,观看人数达到3 150000人。其中3 150 000这个数用科学记数法表示为( )A、0.315×107 B、3.15×106 C、3.15×107 D、315×1043. 如图,在有序号的小正方形中选出一个,它与图中五个有阴影的小正方形组合后,不能构成正方体的表面展开图的是( )
 A、① B、② C、③ D、④4. 不等式3x>-3的解集在数轴上表示正确的是( )A、
A、① B、② C、③ D、④4. 不等式3x>-3的解集在数轴上表示正确的是( )A、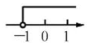 B、
B、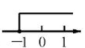 C、
C、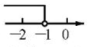 D、
D、 5. 某书店拿取高处书籍的登高梯如图位置摆放,登高梯AC的顶端A恰好放在书架的第七层的顶端,已知登高梯的长度AC为3.2米,登高梯与地面的夹角∠ACB为73°,则书架第七层顶端离地面的高度AB为( )
5. 某书店拿取高处书籍的登高梯如图位置摆放,登高梯AC的顶端A恰好放在书架的第七层的顶端,已知登高梯的长度AC为3.2米,登高梯与地面的夹角∠ACB为73°,则书架第七层顶端离地面的高度AB为( )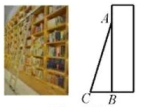 A、3.2cos73°米 B、米 C、3.2sin73°米 D、米6. 如图,在△ABC中,∠BAC=100°,∠ABC=26°,点D在边BC上,连结AD.当AD=AC时,∠ADC的大小为( )
A、3.2cos73°米 B、米 C、3.2sin73°米 D、米6. 如图,在△ABC中,∠BAC=100°,∠ABC=26°,点D在边BC上,连结AD.当AD=AC时,∠ADC的大小为( )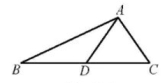 A、54° B、56° C、64° D、74°7. 如图,在ABCD中,AB>AD,按如下步骤作图:①以点A为圆心,AD的长为半径作圆弧,交边AB于点E;②分别以点D和点E为圆心、大于线段DE长的一半为半径作圆弧,两弧交于点P;③作射线AP,交边CD于点F;④连结EF.下列结论不一定成立的是( )
A、54° B、56° C、64° D、74°7. 如图,在ABCD中,AB>AD,按如下步骤作图:①以点A为圆心,AD的长为半径作圆弧,交边AB于点E;②分别以点D和点E为圆心、大于线段DE长的一半为半径作圆弧,两弧交于点P;③作射线AP,交边CD于点F;④连结EF.下列结论不一定成立的是( ) A、AE=AD B、AF=AB C、EF=BC D、AD=DF8. 如图,在平面直角坐标系中,反比例函数y=(k为常数)的图象与正比例函数y=x的图象交于A、B两点.若AB=2 , 则k的值为( )
A、AE=AD B、AF=AB C、EF=BC D、AD=DF8. 如图,在平面直角坐标系中,反比例函数y=(k为常数)的图象与正比例函数y=x的图象交于A、B两点.若AB=2 , 则k的值为( ) A、4 B、2 C、 D、1
A、4 B、2 C、 D、1二、填空题(本大题共6小题,每小题3分,共18分)
-
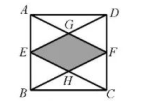
9. 分解因式: -9= .10. 已知一个三角形的两边长分别为2和5,若第三边的长为整数,则第三边的长可以为(写出一个即可)11. 《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:矩形门的高比宽多6尺,门的对角线长为10尺,那么门的高和宽各是多少尺?如果设门的高为x尺,那么根据题意,可列方程为12. 如图,点E、F分别是正方形ABCD的边AB、CD的中点,连结AF、BF、CE、DE,AF与DE相交于点G,BF与CE相交于点H.若AB=1,则四边形EHFG的面积为
 13. 如图,在△ABC中,BC=5,点I为△ABC的内心。将△ABC平移到△IDE的位置,点A的对应点为点I,则图中阴影部分图形的周长为
13. 如图,在△ABC中,BC=5,点I为△ABC的内心。将△ABC平移到△IDE的位置,点A的对应点为点I,则图中阴影部分图形的周长为 14. 在平面直角坐标系中,抛物线y=x2-bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为
14. 在平面直角坐标系中,抛物线y=x2-bx+c(b>0,b、c为常数)的顶点为A,与y轴交于点B,点B关于抛物线对称轴的对称点为C.若△ABC是等腰直角三角形,则BC的长为三、解答题(本大题共10小题,共78分)
-
15. 先化简,再求值:m(m-4)+(m+2)2-1,其中m= .16. 如图,在4X4的正方形网格中,每个小正方形的边长均为1个单位长度,小正方形的顶点称为格点,点A、O均在格点上,小乌龟初始位于点O,它的每一步都会在以下三种情形中随机地选择一种:①向左移动1个单位长度(记为左);②向上移动1个单位长度(记为上);③向右移动1个单位长度(记为右) .用画树状图(或列表)的方法,求小乌龟两步之后到达点A的概率.
 17. 长春冰雪新天地是美丽春城的一道亮丽的风景线,它的设计和造型每年都有变化.在2021年长春冰雪新天地的建造过程中,某工程公司承担了为某项建设取600吨冰块的任务,由于任务紧急,实际取冰时的工作效率比原计划提高了20%,结果提前1天完成任务.该公司原计划每天取冰块多少吨?18. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交边BC于点D,O为边AB上一点,以点O为圆心,OA长为半径的圆恰好经过点D.
17. 长春冰雪新天地是美丽春城的一道亮丽的风景线,它的设计和造型每年都有变化.在2021年长春冰雪新天地的建造过程中,某工程公司承担了为某项建设取600吨冰块的任务,由于任务紧急,实际取冰时的工作效率比原计划提高了20%,结果提前1天完成任务.该公司原计划每天取冰块多少吨?18. 如图,在△ABC中,∠ACB=90°,AD平分∠BAC,交边BC于点D,O为边AB上一点,以点O为圆心,OA长为半径的圆恰好经过点D.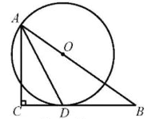 (1)、求证: BC是⊙O的切线.(2)、若⊙O的半径为2,AC=3,则AB的长为19. 初三学生小明就如何分配周末自主复习语文、数学、英语的时间问题,去请教了班主任.班主任结合小明本学期三次模拟考试的成绩,建议他根据“相对失分比”的情况,划分周末复习时间.
(1)、求证: BC是⊙O的切线.(2)、若⊙O的半径为2,AC=3,则AB的长为19. 初三学生小明就如何分配周末自主复习语文、数学、英语的时间问题,去请教了班主任.班主任结合小明本学期三次模拟考试的成绩,建议他根据“相对失分比”的情况,划分周末复习时间.具体操作分为四步:
第一步:计算小明这三次模拟考试中语文、数学、英语单科成绩与当次考试该科年级最高分的差值作为“相对失分”,并记录如下:
小明这三次模拟考试中语文、数学、英语每科成绩“相对失分”表.
学科
相对失分
模拟次数
语文
数学
英语
第一次
15
13
5
第二次
8
14
7
和三次
13
9
6
第二步:计算表中每科成绩的“相对失分”的平均数,并分别记作:语文,数学,英语;
第三步:计算表中每科成绩的“相对失分比”;
某一科成绩的“相对失分比”= ×100%
例:语文成绩的“相对失分比”=×100%.
第四步:根据“相对失分比”划分复习时间,即某科的“相对失分比”就是该科周末复习时间的占比.
根据以上操作步骤,解答下列问题:
(1)、小明的语文三次成绩“相对失分”的平均数语文=分.(2)、小明想通过扇形统计图直观地显示语文、数学、英语每科成绩“相对失分比”的情况,请分别计算小明这三科每科成绩的“相对失分比”,并绘制扇形统计图. (3)、假设小明周末复习语文、数学、英语三科的时间共有200分钟,那么按照上述方法,小明应分配给语文学科的复习时间约为分钟.20. 图①、图②、图③分别是6×6的正方形网格,网格中每个小正方形的边长均为1,小正方形的顶点称为格点,点A、B、C、D、E、P、Q、M、N均在格点上,仅用无刻度的直尺在下列网格中按要求作图,保留作图痕迹.
(3)、假设小明周末复习语文、数学、英语三科的时间共有200分钟,那么按照上述方法,小明应分配给语文学科的复习时间约为分钟.20. 图①、图②、图③分别是6×6的正方形网格,网格中每个小正方形的边长均为1,小正方形的顶点称为格点,点A、B、C、D、E、P、Q、M、N均在格点上,仅用无刻度的直尺在下列网格中按要求作图,保留作图痕迹. (1)、在图①中,画线段AB的中点F.(2)、在图②中,画△CDE的中位线GH,点G、H分别在线段CD、CE上,并直接写出△CGH与四边形DEHG的面积比.(3)、在图③中,画△PQR,点R在格点上,且△PQR被线段MN分成的两部分图形的面积比为1:3.21. 已知A、B两地之间有一条笔直公路,甲车从A地出发匀速去往B地,到达B地后立即以原速原路返回A地,乙车从B地出发匀速去往A地,两车同时出发,乙车比甲车晚20分钟到达A地、甲车距A地的路程y(千米)与甲车行驶的时间x(分钟)之间的函数关系如图所示.
(1)、在图①中,画线段AB的中点F.(2)、在图②中,画△CDE的中位线GH,点G、H分别在线段CD、CE上,并直接写出△CGH与四边形DEHG的面积比.(3)、在图③中,画△PQR,点R在格点上,且△PQR被线段MN分成的两部分图形的面积比为1:3.21. 已知A、B两地之间有一条笔直公路,甲车从A地出发匀速去往B地,到达B地后立即以原速原路返回A地,乙车从B地出发匀速去往A地,两车同时出发,乙车比甲车晚20分钟到达A地、甲车距A地的路程y(千米)与甲车行驶的时间x(分钟)之间的函数关系如图所示. (1)、在图中画出乙车距A地的路程y(千米)与x(分钟)之间的函数图象,并求出它所对应的函数关系式.(写出自变量x的取值范围)(2)、甲、乙两车在行驶过程中相遇了次.(3)、求甲车到B地时,乙车距A地的路程.22. [问题呈现]小强在一次学习过程中遇到了下面的问题:
(1)、在图中画出乙车距A地的路程y(千米)与x(分钟)之间的函数图象,并求出它所对应的函数关系式.(写出自变量x的取值范围)(2)、甲、乙两车在行驶过程中相遇了次.(3)、求甲车到B地时,乙车距A地的路程.22. [问题呈现]小强在一次学习过程中遇到了下面的问题:
如图①,在△ABC与ODEF中,AB=DE,∠A=∠D,AC+BC=DF.
求证:∠ACB=2∠F.
(1)、[方法探究]以下是小强的方法:证明:如图②,延长AC到点G,使CG=CB,连结BG.
∵CG=CB,
∴∠CBG=∠G .
∴∠ACB=∠CBG+∠G=2∠G.
接下来只需证明∠G=∠F,进而就能得出∠ACB=2∠F .
请你补全余下的证明过程.
(2)、[方法总结]从上面的方法可以看出,通过“化折为直”,不仅可以构造等腰三角形,还可以得到角的倍、半关系,可谓一举两得.[方法应用]如图③,在△ABC中,∠ACB=90°,∠A=35°,延长BC到点D,使DC=BC,点E在边AC上,连结DE.当DE+EC=AC时,∠DEC的大小为°
 (3)、[拓展延伸]如图④,在△ABC中,∠C=90°,∠B=50°.若AB+BC=10,求边AC的长.(精确到 0.1)
(3)、[拓展延伸]如图④,在△ABC中,∠C=90°,∠B=50°.若AB+BC=10,求边AC的长.(精确到 0.1)[参考数据:sin25°≈0.423,cos25°≈ 0.906,tan25°≈0.466 ]
23. 如图,ABCD的面积为12,AB=6,AD=3.点M在边AB上(点M与点A不重合),连结DM,作点A关于直线DM的对称点A',连结AM、AD. (1)、点D到直线AB的距离是 .(2)、设点A'到直线BC的距离为d,求d的最小值.(3)、当点A'落在 ABCD的边上时,求AM的长.(4)、当直线A'M与 ABCD的一边垂直时,直接写出AM的长.24. 在平面直角坐标系中,抛物线y=x2+bx+c (b、c为常数)的对称轴为直线x=1,与y轴交点的坐标为(0,-2),点A、点B均在这个抛物线上(点A在点B的左侧),点A的横坐标为m,点B的横坐标为1-2m.(1)、求此抛物线对应的函数表达式.(2)、当点A、点B关于此抛物线的对称轴对称时,连结AB,求线段AB的长.(3)、将此抛物线上A、B两点之间的部分(包括A、B两点)记为图象G.
(1)、点D到直线AB的距离是 .(2)、设点A'到直线BC的距离为d,求d的最小值.(3)、当点A'落在 ABCD的边上时,求AM的长.(4)、当直线A'M与 ABCD的一边垂直时,直接写出AM的长.24. 在平面直角坐标系中,抛物线y=x2+bx+c (b、c为常数)的对称轴为直线x=1,与y轴交点的坐标为(0,-2),点A、点B均在这个抛物线上(点A在点B的左侧),点A的横坐标为m,点B的横坐标为1-2m.(1)、求此抛物线对应的函数表达式.(2)、当点A、点B关于此抛物线的对称轴对称时,连结AB,求线段AB的长.(3)、将此抛物线上A、B两点之间的部分(包括A、B两点)记为图象G.①当图象G对应的函数值y随x的增大而先减小后增大时,设图象G最高点的纵坐标与最低点的纵坐标的差为h,求h与m之间的函数关系式,并写出h的取值范围.
②设点E的坐标为(-2-2m,1),点F的坐标为(-2-2m,-3-2m),连结EF,当线段EF和图象G有公共点时,直接写出m的取值范围.