浙江省金华十校2023届高三下学期数学4月模拟试卷

试卷更新日期：2023-04-25 类型：高考模拟

进入出卷网下载

一、单选题

1. 设i为虚数单位，复数z满足 $i z + 1 = (1 - i)^{2}$ ，则 $| 1 + z | =$ （）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{5}$ D、 $2 \sqrt{3}$

查看试题解析
2. 若集合 $A = {x ∣ \frac{x + 1}{x - 2} \leq 0} ， B = {x ∣ l o g_{2} x \leq 1}$ ，则 $A ∩ B =$ （）

A、 $[- 1 ， 2]$ B、 $(- 1 ， 2)$ C、 $[0 ， 2]$ D、 $(0 ， 2)$

查看试题解析
3. 已知向量 $\vec{a} = (c o s θ ， s i n θ) ， \vec{b} = (\sqrt{2} ， 1)$ ，若 $\vec{a} \cdot \vec{b} = | \vec{b} |$ ，则 $t a n θ =$ （）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
4. 已知函数 $f (x) = s i n ω x - c o s (ω x + \frac{π}{6}) (ω > 0)$ 在 $[0 ， π]$ 上有且仅有2个零点，则 $ω$ 的取值范围是（）

A、 $[1 ， \frac{13}{6}]$ B、 $[\frac{7}{6} ， \frac{13}{6})$ C、 $[\frac{7}{6} ， 2)$ D、 $[1 ， \frac{13}{6})$

查看试题解析
5. 已知函数 $f (x) = x^{3} - 3 x^{2}$ ，则（）

A、函数 $f (x)$ 的极大值点为 $(0 ， 0)$ B、函数 $f (x)$ 的极小值为2 C、过点 $(- 1 ， 0)$ 作曲线 $y = f (x)$ 的切线有两条 D、直线 $3 x + y - 1 = 0$ 是曲线 $y = f (x)$ 的一条切线

查看试题解析
6. 魔方，又叫鲁比克方块，最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授于1974年发明的机械益智玩具．魔方拥有竞速、盲拧、单拧等多种玩法，风靡程度经久未衰，每年都会举办大小赛事，是最受欢迎的智力游戏之一，一个三阶魔方，由27个单位正方体组成，如图是把魔方的中间一层转动了 $45 °$ ，则该魔方的表面积是（）

A、54 B、 $108 - 36 \sqrt{2}$ C、 $162 - 72 \sqrt{2}$ D、 $81 - 72 \sqrt{2}$

查看试题解析
7. 三棱锥 $P - A B C$ 中， $A B ⊥ A C ， A B = 2 ， B C = 2 \sqrt{2} ， P C ⊥ A C ， P B = 2 \sqrt{5}$ ，则三棱锥 $P - A B C$ 的外接球表面积的最小值为（）

A、 $16 π$ B、 $18 π$ C、 $20 π$ D、 $21 π$

查看试题解析
8. “清明时节雨纷纷，路上行人欲断魂”描述的是我国传统节日“清明节”的景象．“青团”创于宋朝，是清明节的寒食名点之一，也是人们提起清明节会最先想到的美食．某地居民喜好的青团品种有4个，假定每个人购买时对于每种青团的选择是独立的，选择每个品种的概率均为 $\frac{1}{3}$ ，若在清明节当日，某传统糕点店为顾客只准备了3个品种的青团，则一位进店顾客，他的要求可以被满足的概率为（）

A、 $\frac{14}{81}$ B、 $\frac{10}{27}$ C、 $\frac{38}{81}$ D、 $\frac{2}{3}$

查看试题解析

二、多选题

9. 在单位正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，O为底面ABCD的中心，M为线段 $C C_{1}$ 上的动点（不与两个端点重合），P为线段BM的中点，则（）

A、直线DP与OM是异面直线 B、三棱锥 $B_{1} - D B M$ 的体积是定值 C、存在点M，使 $A C_{1} / /$ 平面BDM D、存在点M，使 $A_{1} C ⊥$ 平面BDM

查看试题解析
10. 已知 $A (x_{0} ， y_{0}) ， B ， C$ 为抛物线 $y^{2} = 4 x$ 上的三个点，焦点F是 $△ A B C$ 的重心．记直线AB，AC，BC的斜率分别为 $k_{A B} ， k_{A C} ， k_{B C}$ ，则（）

A、线段BC的中点坐标为 $(\frac{12 - y_{0}^{2}}{8} ， - \frac{y_{0}}{2})$ B、直线BC的方程为 $4 x + y_{0} y + y_{0}^{2} - 6 = 0$ C、 $y_{0} \in [- 2 \sqrt{3} ， 2 \sqrt{3}]$ D、 $\frac{1}{k_{A B}} + \frac{1}{k_{A C}} - \frac{1}{k_{B C}} = \frac{y_{0}}{2}$

查看试题解析
11. 已知函数 $f_{1} (x) = - x^{2} + 1 ， x \in [- 1 ， 1)$ ，记一次完整的图形变换为“T变换”，“T变换”的规则为：将函数图象向右平移2个单位，纵坐标缩短为原来的 $\frac{1}{2}$ ，再向上平移1个单位， $f_{1} (x)$ 的图象经历一次“T变换”得到 $f_{2} (x)$ 的图象，依此类推，经历 $n - 1$ 次“T变换”后，得到 $f_{n} (x)$ 的图象，则（）

A、 $f_{2} (x) = - \frac{1}{2} x^{2} + 2 x - \frac{1}{2} ， x \in [1 ， 3)$ B、若 $f_{i} (x) \leq k (x + 2) ， i = 1 ， 2 ， ⋯ ， n$ ，则 $k \geq \frac{1}{2}$ C、当 $n \geq 2$ 时，函数 $f_{1} (x) ， f_{2} (x) ， ⋯ ， f_{n} (x)$ 的极大值之和小于 $2 n - 1$ D、 $f_{n} (x) < 2$

查看试题解析
12. 已知定义在 $R$ 上且不恒为 $0$ 的函数 $f (x)$ ，若对任意的 $x ， y \in R$ ，都有 $f (x y) = x f (y) + y f (x)$ ，则（）

A、函数 $f (x)$ 是奇函数 B、对 $\forall n \in N^{*}$ ，有 $f (x^{n}) = n f (x)$ C、若 $f (2) = 2$ ，则 $f (2) + f (2^{2}) + f (2^{3}) + ⋯ + f (2^{n}) = (n + 1) 2^{n} - 2$ D、若 $f (2) = 2$ ，则 $\frac{f (\frac{1}{2})}{1} + \frac{f ({(\frac{1}{2})}^{2})}{2} + \frac{f ({(\frac{1}{2})}^{3})}{3} + ⋯ + \frac{f ({(\frac{1}{2})}^{10})}{10} = - \frac{1023}{1024}$

查看试题解析

三、填空题

13. $9 9^{100}$ 除以100的余数是．

查看试题解析
14. 折纸是很多人喜爱的游戏，通过自己动手折纸，可以激发和培养审美情趣，锻炼双手，开发智力，提高实践技能．一张圆形纸片的半径为 $8$ ，圆心 $O$ 到定点 $A$ 的距离为 $6$ ，在圆周上任取一点 $P$ ，将圆形纸片折起，使得 $P$ 与 $A$ 重合，折痕记为直线 $l$ ，直线 $l$ 与直线 $O P$ 的交点为 $Q$ ．将此操作多次重复，则 $Q$ 点的轨迹是（填“圆”、“椭圆”、“双曲线”、“抛物线”）

查看试题解析
15. 若关于x的不等式 $a l n \frac{\sqrt{x}}{e} \leq x$ 恒成立，则a的取值范围是．

查看试题解析
16. 已知椭圆 $G ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点为F，左右顶点分别为A，B，点P是椭圆G上异于A，B的动点，过F作直线AP的垂线交直线BP于点 $M (m ， n)$ ，若 $m + a = 0$ ，则椭圆G的离心率为．

查看试题解析

四、解答题

17. 在等差数列 ${a_{n}}$ 中， $a_{4} = 4 ， S_{n}$ 为 ${a_{n}}$ 的前n项和， $S_{10} = 55$ ，数列 ${b_{n}}$ 满足 $l o g_{2} b_{1} + l o g_{2} b_{2} + ⋯ + l o g_{2} b_{n} = \frac{n (n + 1)}{2}$ ．

(1)、求数列 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、求数列 ${(- 1)^{n} a_{n} b_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
18. 在 $△ A B C$ 中，角A，B，C所对应的边为a，b，c．已知 $△ A B C$ 的面积 $S = \frac{a c}{4}$ ，其外接圆半径 $R = 2$ ，且 $4 (c o s^{2} A - c o s^{2} B) = (b - \sqrt{3} a) s i n B$ ．

(1)、求 $s i n A$ ；

(2)、若A为钝角，P为 $△ A B C$ 外接圆上的一点，求 $\vec{P A} \cdot \vec{P B} + \vec{P B} \cdot \vec{P C} + \vec{P C} \cdot \vec{P A}$ 的取值范围．

查看试题解析
19. 如图，在圆台 $O_{1} O_{2}$ 中，圆 $O_{1}$ 的半径是1，圆 $O_{2}$ 的半径是2，高是 $\sqrt{3}$ ，圆 $O_{1}$ 是 $△ A B C$ 的外接圆， $A B = \sqrt{3}$ ， PC是圆台的一条母线．

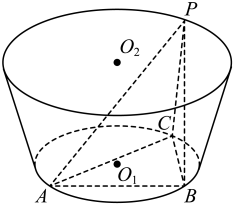(1)、求三棱锥 $P - A B C$ 体积的最大值；

(2)、当 $P A = 2 \sqrt{3}$ 时，求平面PAC与平面PBC的锐二面角的余弦值．

查看试题解析
20. 全国 “两会”召开的一项重要意义在于将“两会代表”从人民中得来的信息和要求进行收集及整理，传达给中央，“两会代表”代表着广大选民的利益，代表选民在“两会”期间向政府有关部门提出选民的意见和要求．下表是2011年至2020年历年全国政协提案的数量统计．
年份
2011
2012
2013
2014
2015
2016
2017
2018
2019
2020
年份代码x
1
2
3
4
5
6
7
8
9
10
提案数量y（单位：千件）
5.762
6.069
5.641
5.875
5.857
5.769
5.21
5.36
5.488
5.044
参考公式：相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sqrt{(\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}) \sqrt{(\sum_{i = 1}^{n} y_{i}^{2} - n {\bar{y}}^{2})}}}$ ， $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} ， \hat{a} = \bar{y} - \hat{b} x$ ．
参考数据： $\sum_{i = 1}^{10} x_{i} y_{i} \approx 301.4 ， 10 \bar{x} \bar{y} \approx 308.4 ， \sum_{i = 1}^{10} y_{i}^{2} - 10 {\bar{y}}^{2} \approx 0.95 ， \bar{y} \approx 5.61 ， \sqrt{82.5} \times \sqrt{0.95} \approx 8.85$ ．

(1)、请用相关系数说明y与x之间的关系可否用线性回归模型拟合？若能，求y关于x的一元线性回归方程；（运算结果精确到0.01）（若 $| r | \geq 0 ． 75$ ，则线性相关程度很高，可用直线拟合）

(2)、中央政府回应2020年“两会”的热点议题“战胜疫情”，以令世界惊叹的中国速度、中国效率和中国奇迹，社会各阶层、各行各业迅速投身战“疫”行动，团结共进、众志成城．其中一个关键举措是2021年全国各地全面展开的疫苗接种．为方便市民合理安排疫苗接种，城市便民电子系统即时提供接种点相关信息，若某疫苗接种点上午和下午接种疫苗分别需要等待20分钟和40分钟，而甲、乙市民均在某日接种疫苗，且上午去接种疫苗的概率分别为 $p ， 2 p - 1 (\frac{1}{2} < p < 1)$ ，要使两市民需要等待时间的总和的期望值不超过60分钟，求实数p的取值范围．

查看试题解析
21. P是双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{12} = 1$ 右支上一点，A，B是双曲线的左右顶点，过A，B分别作直线PA，PB的垂线AQ，BQ，AQ与BQ的交点为Q，PA与BQ的交点为C．

(1)、记P，Q的纵坐标分别为 $y_{P} ， y_{Q}$ ，求 $\frac{y_{P}}{y_{Q}}$ 的值；

(2)、记 $△ P B C ， △ Q A C$ 的面积分别为 $S_{1} ， S_{2}$ ，当 $\frac{1}{2} \leq t a n ∠ A Q B \leq \frac{\sqrt{15}}{5}$ 时，求 $\frac{S_{1}}{S_{2}}$ 的取值范围．

查看试题解析
22. 已知函数 $f (x) = a s i n x - l n (1 + x) ， a \in R$ ．

(1)、若对 $\forall x \in (- 1 ， 0]$ 时， $f (x) \geq 0$ ，求正实数a的最大值；

(2)、证明： $\sum_{i = 2}^{n} s i n \frac{1}{i^{2}} < l n 2$ ；

(3)、若函数 $g (x) = f (x) + e^{x + 1} - a s i n x$ 的最小值为m，证明：方程 $e^{1 + x - m} - l n (1 + x) = 0$ 有唯一的实数根，（其中 $e = 2.71828 ⋯$ 是自然对数的底数）

查看试题解析

年份	2011	2012	2013	2014	2015	2016	2017	2018	2019	2020
年份代码x	1	2	3	4	5	6	7	8	9	10
提案数量y（单位：千件）	5.762	6.069	5.641	5.875	5.857	5.769	5.21	5.36	5.488	5.044