上海市松江区2023届高三数学二模试卷
试卷更新日期:2023-04-25 类型:高考模拟
一、填空题
-
1. 已知集合 , , 则 .2. 若复数z满足 , 则3. 已知空间向量 , , , 若 , 则 .4. 已知随机变量X服从正态分布 , 若 , 则 .5. 已知 , 且 , 则 .6. 在的展开式中,的系数为 . (用数字作答)7. 将下图所示的圆锥形容器内的液体全部倒入底面半径为的直立的圆柱形容器内,则液面高度为 .
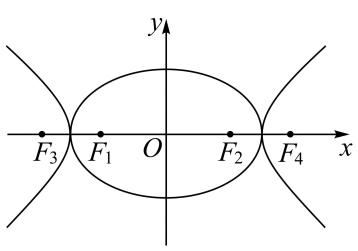
 8. 现从名男医生和名女医生中抽取两人加入“援沪医疗队”,用表示事件“抽到的两名医生性别同”,表示事件“抽到的两名医生都是女医生”,则.9. 参考《九章算术》中“竹九节”问题,提出:一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共2升,下面3节的容积共3升,则第5节的容积为升.10. 若 , 则的最小值为11. 已知函数为上的奇函数;且 , 当时, , 则 .12. 已知点是平面直角坐标系中关于轴对称的两点,且 . 若存在 , 使得与垂直,且 , 则的最小值为 .
8. 现从名男医生和名女医生中抽取两人加入“援沪医疗队”,用表示事件“抽到的两名医生性别同”,表示事件“抽到的两名医生都是女医生”,则.9. 参考《九章算术》中“竹九节”问题,提出:一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共2升,下面3节的容积共3升,则第5节的容积为升.10. 若 , 则的最小值为11. 已知函数为上的奇函数;且 , 当时, , 则 .12. 已知点是平面直角坐标系中关于轴对称的两点,且 . 若存在 , 使得与垂直,且 , 则的最小值为 .二、单选题
-
13. 已知直线与直线 , 则“”是“”的( )A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件14. 为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元)
8.2
8.6
10.0
11.3
11.9
支出y(万元)
6.2
7.5
8.0
8.5
9.8
根据上表可得回归直线方程 , 其中 , , 据此估计,该社区一户收入为15万元家庭年支出为( )
A、11.4万元 B、11.8万元 C、12.0万元 D、12.2万元15. 若方程的解集为M,则以下结论一定正确的是( )
(1)
(2)
(3)
(4)A、(1)(4) B、(2)(4) C、(3)(4) D、(1)(3)(4)16. 已知函数 , , 在区间上有最大值,则实数t的取值范围是( )A、 B、 C、 D、三、解答题
-
17. 在锐角中,内角A、B、C所对边分别为a、b、c,且 .(1)、求角B;(2)、求的最大值.18. 如图,在四棱锥中,底面ABCD为平行四边形,O是AC与BD的交点, , , 平面ABCD, , M是PD的中点.
 (1)、证明:平面ACM(2)、求直线AM与平面ABCD所成角的大小.19. 某城市响应国家号召,积极调整能源结构,推出多种价位的新能源电动汽车.根据前期市场调研,有购买新能源车需求的约有2万人,他们的选择意向统计如下:
(1)、证明:平面ACM(2)、求直线AM与平面ABCD所成角的大小.19. 某城市响应国家号召,积极调整能源结构,推出多种价位的新能源电动汽车.根据前期市场调研,有购买新能源车需求的约有2万人,他们的选择意向统计如下:车型
A
B
C
D
E
F
价格
9万元
12万元
18万元
24万元
30万元
40万元
占比
5%
15%
25%
35%
15%
5%
(1)、如果有购车需求的这些人今年都购买了新能源车,今年新能源车的销售额预计约为多少亿元?(2)、车企推出两种付款方式:全款购车:购车时一次性付款可优惠车价的3%;
分期付款:无价格优惠,购车时先付车价的一半,余下的每半年付一次,分4次付完,每次付车价的 .
①某位顾客现有a万元现金,欲购买价值a万元的某款车,付款后剩余的资金全部用于购买半年期的理财产品(该理财产品半年期到期收益率为1.8%),到期后,可用资金(含理财收益)继续购买半年期的理财产品,问:顾客选择哪一种付款方式收益更多?(计算结果精确到0.0001)
②为了激励购买理财产品,银行对采用分期付款方式的顾客,赠送价值1888元的大礼包,试问:这一措施对哪些车型有效?(计算结果精确到0.0001)