浙江省宁波市鄞州2023年八年级下学期期中联考数学试卷
试卷更新日期:2023-04-25 类型:期中考试
一、选择题(每小题3分,共30分)
-
1. 下列四个生活安全警示图标,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a<b.”时第一步应假设( )A、a>b B、a≥b C、a≤b D、a≠b4. 一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )A、方差 B、平均数 C、中位数 D、众数5. 若关于x的一元二次方程x2+2x-k=0没有实数根,则实数k的取值范围为( )A、k<-1 B、k≤-1 C、k≥-1 D、k>-16. 某商品经过连续两次降价,价格从100元降为64元.已知两次降价的百分率都是x,则x满足的方程是( )A、64(1-2x)=100 B、100(1-x)2=64 C、64(1-x)2=100 D、100(1-2x)=647. 如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB长度10米,则坡面AB的水平宽度AC长为( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 用反证法证明命题:“在△ABC中,∠A,∠B的对边分别是a,b,若∠A<∠B,则a<b.”时第一步应假设( )A、a>b B、a≥b C、a≤b D、a≠b4. 一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )A、方差 B、平均数 C、中位数 D、众数5. 若关于x的一元二次方程x2+2x-k=0没有实数根,则实数k的取值范围为( )A、k<-1 B、k≤-1 C、k≥-1 D、k>-16. 某商品经过连续两次降价,价格从100元降为64元.已知两次降价的百分率都是x,则x满足的方程是( )A、64(1-2x)=100 B、100(1-x)2=64 C、64(1-x)2=100 D、100(1-2x)=647. 如图,大坝横截面的迎水坡AB的坡比为1:2,即BC:AC=1:2,若坡面AB长度10米,则坡面AB的水平宽度AC长为( ) A、 B、5 C、 D、8. 如图,菱形ABCD的顶点A;B分别在y轴正半轴,x轴正半轴上,点C的横坐标为10,点D的纵坐标为8,若直线AC平行x轴,则菱形ABCD的边长值为( )
A、 B、5 C、 D、8. 如图,菱形ABCD的顶点A;B分别在y轴正半轴,x轴正半轴上,点C的横坐标为10,点D的纵坐标为8,若直线AC平行x轴,则菱形ABCD的边长值为( ) A、9 B、 C、6 D、39. 从一块腰长为10cm的等腰直角三角形铁皮零料。上裁出一块面积为24cm2的矩形铁皮,要求矩形的四个顶点都在三角形的边上.若裁出的矩形全等视为同种裁法,则有几种不同的裁法? ( )A、1 B、2 C、3 D、410. 如图,点E是矩形ABCD内一点,连结AE,DE,AC,EC,BE,知道下列哪个选项的值就能要求△AEC的面积( )
A、9 B、 C、6 D、39. 从一块腰长为10cm的等腰直角三角形铁皮零料。上裁出一块面积为24cm2的矩形铁皮,要求矩形的四个顶点都在三角形的边上.若裁出的矩形全等视为同种裁法,则有几种不同的裁法? ( )A、1 B、2 C、3 D、410. 如图,点E是矩形ABCD内一点,连结AE,DE,AC,EC,BE,知道下列哪个选项的值就能要求△AEC的面积( )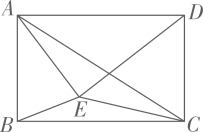 A、△ABE与△BEC面积之差 B、△ADE与△BEC面积之差 C、△DEC与△BEC面积之差 D、△ADC与△DEC面积之差
A、△ABE与△BEC面积之差 B、△ADE与△BEC面积之差 C、△DEC与△BEC面积之差 D、△ADC与△DEC面积之差二、填空题(每小题3分,共18分)
-
11. 化简:=12. 已知一组数据是-1,0,-1,2,则这组数据的方差是13. 若m是方程3x2-x-2=0的一个根,则代数式6m2-2m的值为14. 如图,在四边形ABCD中,∠A+∠C=136°,点E在边AD上,连结BE,若∠D与∠EBC互补,则∠EBA的值为
 15. 如图,用长为a米的铝合金制成如图窗框,已知矩形AGHD,矩形BFEG,矩形EFCH的面积均相等,设AD的长为b米,则AB的长是米.(用含a,b的代数式表示)
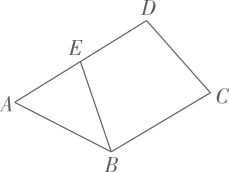
15. 如图,用长为a米的铝合金制成如图窗框,已知矩形AGHD,矩形BFEG,矩形EFCH的面积均相等,设AD的长为b米,则AB的长是米.(用含a,b的代数式表示)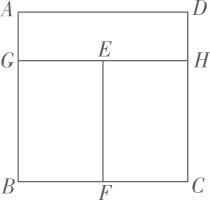 16. 如图,在凸四边形ABCD中,AB=4,AD=2 , CD=2,∠BAD=45°,连结AC,取AC中点E,连结BE,则BE的最小值是
16. 如图,在凸四边形ABCD中,AB=4,AD=2 , CD=2,∠BAD=45°,连结AC,取AC中点E,连结BE,则BE的最小值是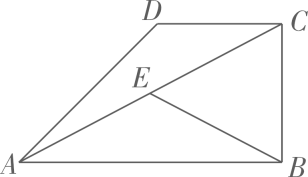
三、解答题(第17~19题各6分,第20~22 题各8分,第23 题10分,共52分)
-
17.(1)、计算:(2)、解方程:(x+3)2-4=018. 图1是由边长为1的正方形构成的6x5的网格图,线段AB的端点都在格点上.
 (1)、在图1中画出一个以AB为一边,面积为12的矩形ABCD,并直接写出矩形ABCD对角线的长为 .(2)、命题“一组对边相等且有一个内角是直角的四边形是矩形”是真命题还是假命题?如果是假命题,请在图2中画一个顶点都是格点的凸四边形说明;若是真命题,请进行证明.19. 某公司需招聘一名员工,对应聘者A、B、C从笔试、面试、体能三个方面进行最化考核.A、B、C各项得分如下表:
(1)、在图1中画出一个以AB为一边,面积为12的矩形ABCD,并直接写出矩形ABCD对角线的长为 .(2)、命题“一组对边相等且有一个内角是直角的四边形是矩形”是真命题还是假命题?如果是假命题,请在图2中画一个顶点都是格点的凸四边形说明;若是真命题,请进行证明.19. 某公司需招聘一名员工,对应聘者A、B、C从笔试、面试、体能三个方面进行最化考核.A、B、C各项得分如下表:笔试
面试
体能
A
82
79
91
B
84
80
76
C
81
90
72
(1)、根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;(2)、该公司规定:笔试、面试、体能得分分别不得低于80分、80 分、70分,并按60%,30%,10%的比例计入总分,总分最高者将被录用,根据规定,请你说明谁将被录用.20. 商场某种商品平均每天可售出30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)、商场日销售增加件,每件商品盈利元;(2)、在上述条件不变,销售情况正常情况下,当每件商品降价多少元时,商场日盈利可达2100元?21. 如图,在矩形ABCD中,点E,F分别在AD,BC上,且AE=CF. (1)、求证:四边形BFDE是平行四边形:(2)、若AB=2,AD=4,四边形BFDE是菱形,求AE长.22. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.
(1)、求证:四边形BFDE是平行四边形:(2)、若AB=2,AD=4,四边形BFDE是菱形,求AE长.22. 我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用.例如:已知x可取任何实数,试求二次三项式x2+2x+3的最小值.
解:x2+2x+3=x2+2x+1+2=(x+1)2+2
∵无论x取何实数,都有(x+1)2≥0,
∴(x+1)2+2≥2,即x2+2x+3的最小值为2.
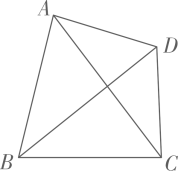
(1)、[尝试应用]请直接写出2x2+4x+10的最小值;(2)、[拓展应用]试说明:无论x取何实数,二次根式4都有意义;(3)、[创新应用]如图,在四边形.ABCD中,AC⊥BD,若AC+BD=10,求四边形ABCD的面积最大值.
 23. 如图,在边长为4的正方形ABCD中,点E在边AD上,DE=1,连结BE,点P,点F分别是线段BE,边CD上的动点.
23. 如图,在边长为4的正方形ABCD中,点E在边AD上,DE=1,连结BE,点P,点F分别是线段BE,边CD上的动点. (1)、连结AP,PF,若A,P,F三点共线,且AF=BE.
(1)、连结AP,PF,若A,P,F三点共线,且AF=BE.①求证:BE⊥AF;
②求PF的长;
(2)、如图2,若CF=1,∠EPF=45°,则PF的长为.(3)、问题:“如图3,若CF=1,直线PF刚好平分正方形ABCD的面积,求PF的长.”在解决这一问题时,小红想先找到对应的点P,然后再求PF的长.经过不断的思考探索后,小红尝试以B为原点,建立坐标系来解决这一问题.请你帮助小红用无刻度的直尺在图3中找到点P,并直接写出PF的长为.