浙江省宁波市海曙区2022-2023学年七年级下学期数学期中联考试卷

试卷更新日期：2023-04-25 类型：期中考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 仔细观察下列图形，其中∠1与∠2是内错角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，属于二元一次方程的是（）

A、2x-1=3 B、x+y-z=1 C、2x-3=y D、x- $\frac{1}{y}$ =1

查看试题解析
3. 下列计算正确的是（）

A、2m²·3m³= 6m⁶ B、m·m⁵=(-m³)² C、(-3mn)³=-9m³n³ D、(-2mn²)²=4m²n²

查看试题解析
4. 下列等式中，从左到右的变形属于因式分解的是（）

A、x+2y=(x+y)+y B、p(q+h)=pq+ph C、4a²-4a+1=4a(a-1)+1 D、5x²y-10xy²=5xy(x-2y)

查看试题解析
5. 一种花粉颗粒直径约为0.0000065米，数字0.0000065用科学记数法表示为（）

A、0.65×10^-5 B、65×10^-7 C、6.5×10^-6 D、6.5×10^-5

查看试题解析
6. 若s+t=4，则s²-t²+8t的值是（）

A、8 B、12 C、16 D、32

查看试题解析
7. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为（2a+3b），宽为（a+2b）的大长方形，则需要A类、B类和C类卡片的张数分别为（）

A、 $2$ ， $8$ ， $5$ B、 $3$ ， $8$ ， $6$ C、 $3$ ， $7$ ， $5$ D、 $2$ ， $6$ ， $7$

查看试题解析
8. 若(x-2)(x²-mx+1)的展开式中不含x的二次项，则化简后的一次项系数是（）

A、-3 B、-2 C、 $- \frac{1}{2}$ D、 $- \frac{3}{2}$

查看试题解析
9. 若m，n均是正整数，且2^m+1×4ⁿ=128，则m+n的所有可能值为（）

A、5或4 B、3或4 C、2或3 D、6或5

查看试题解析
10. 如图，AB∥CD，点P在AB，CD之间，∠ACP=2∠PCD=40°，连结AP，若∠BAP=α，∠CAP=α+β．下列说法中正确的是（）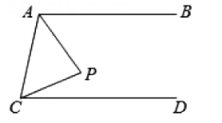

A、当∠P=60°时，α=30° B、当∠P=60°时，β=40° C、当=20°时，∠P=90° D、当β=0°时，∠P=90°

查看试题解析

二、填空题(每小题3分，共18分)

11. 计算：(-2)²⁰²³×( $\frac{1}{2}$ )²⁰²³=

查看试题解析
12. 计算： $16 y^{2} \div (8 y) =$ .

查看试题解析
13. 将4x-3y=5变形成含x的代数式表示y，则y=

查看试题解析
14. 如果多项式4x²-(1-m)x+9是一个完全平方式，则常数m的值是

查看试题解析
15. 已知关于x， y的二元一次方程组 ${\begin{cases} 3 x + y = 2 k ， \\ x - 2 y = k + 6 \end{cases}$ 有下列说法：①当x与y相等时，解得k=-4；②当x与y互为相反数时，解得k=3；③若4^x·8^y=32，则k=11；④无论k为何值，x与y的值一定满足关系式x+5y+12=0，其中正确的序号是

查看试题解析
16. 如图有两张正方形纸片A和B，图1将B放置在A内部，测得阴影部分面积为3；图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为21；若将3个正方形A和2个正方形B并列放置后构造新正方形如图3 (图2，图3中正方形AB纸片均无重叠部分)，则图3阴影部分面积是

查看试题解析

三、解答题(第17-22题，每小题6分，第23、24题，每小题8分，共52分)

17. 分解因式：

(1)、x²y-y

(2)、ax²-6ax+9a

查看试题解析
18. 解方程组

(1)、 ${\begin{array}{l} x - 2 y = 3 \\ x + 4 y = - 3 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x - 1}{2} + \frac{y + 1}{3} = 1 \\ x + y = 4 \end{array}$

查看试题解析
19. 计算：

(1)、(-1)²⁰²³-( $\sqrt{2}$ -1)⁰

(2)、(15x³y⁵-10x⁴y⁴-20x³y²) ÷(-5x³y²)

查看试题解析
20. 先化简，再求值：(x-2)(3x²-1)-12×( $\frac{1}{4}$ x²- $\frac{1}{2}$ x-3)，其中x= $- \frac{1}{5}$

查看试题解析
21. 如图所示，有-块边长为(3a+b)米和(a+2b) 米的长方形土地，现准备在这块土地上修建一个长为(2a+b)米，宽为(a+b)米的游泳池，剩余部分修建成休息区域．

(1)、请用含a和b的代数式表示休息区域的面积； (结果要化简)

(2)、若a=5，b=10，求休息区域的面积．

查看试题解析
22. 某冬奥会纪念品专卖店计划同时购进“冰墩墩”和“雪容融”两种毛绒玩具．据了解，8只“冰墩墩”和10只“雪容融”的进价共计2000元；10只“冰墩墩”和20只“雪容融”的进价共计3100元．

(1)、求“冰墩墩”和“雪容融”两种毛绒玩具每只进价分别是多少元；

(2)、该专卖店计划恰好用3500元购进“冰墩墩”和“雪容融”两种毛绒玩具(两种均购买)，求专卖店共有几种采购方案．

查看试题解析
23. 如图

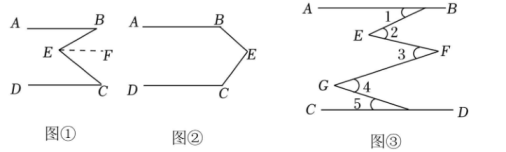(1)、问题发现：
如图①，直线AB∥CD，连接BE，CE，可以发现∠B+∠C=∠BEC．请把下面的证明过程补充完整：
证明：过点E作EF∥AB，
∵AB∥DC (已知)
∴EF∥DC（）．
∴∠C=∠CEF．（）．
∵EF∥AB，
∴∠B=∠BEF(同理)．
∴∠B+∠C= ▲ (等量代换)．即∠B+∠C=∠BEC．

(2)、拓展探究：
如果点E运动到图②所示的位置，其他条件不变，说明：∠B+∠C+∠BEC=360°．

(3)、解决问题：如图③，AB∥DC，E、F、G是AB与CD之间的点，直接写出∠1，∠2，∠3，∠4，∠5之间的数量关系．

查看试题解析
24. [学习材料]拆项添项法
在对某些多项式进行因式分解时，需要把多项式中的某一项拆成两项或多项，或者在多项式中添上两个仅符号相反的项，这样的分解因式的方法称为拆项添项法。如：

例1、分解因式：x⁴+4y⁴

解：原式=x⁴+4y⁴=x⁴+4x²y²+4y⁴-4x²y²

=(x²+2y²)²-4x²y²=(x²+2y²+2xy)(x²+2y²-2xy)

例2、分解因式：x³+5x-6

解：原式=x³-x+6x-6=x(x²-1)+6(x-1)=(x-1)(x²+x+6)

我们还可以通过拆项对多项式进行变形，如

例3、把多项式a²+b²+4a-6b+13写成A²+B²的形式．

解：原式=a²+4a+4+b²-6b+9=(a+2)²+(b-3)²

[知识应用]请根据以上材料中的方法，解决下列问题：

(1)、分解因式：x²+2x-8=

(2)、分解因式：x⁴+4=

(3)、关于x的二次三项式x²-20x+111在x=时，有最小值；

(4)、已知M=x²+6x+4y²-12y+m(x-y均为整数，m是常数)，若M恰能表示成A²+B²的形式，求m的值．

查看试题解析